· Educație - repetarea, generalizarea și testarea cunoștințelor pe tema: "Metoda locurilor geometrice", dezvoltarea abilităților de bază.
· Dezvoltarea - pentru a dezvolta atenția elevilor, perseverența, perseverența, gândirea logică, vorbirea matematică.
· Educația - prin lecție de a educa o relație atentă una cu cealaltă, de a încuraja capacitatea de a asculta tovarăși, asistență reciprocă, independență.
I. Stadiul organizațional (2 min)
II.Aktualizatsija experiența subiectului elevilor (5 mine).
1) Ce este un cerc?
2) da definiția unui triunghi?
3) Ce este o perpendiculară?
4) Care este tangenta?
5) Care este bisectorul triunghiului?
Formarea aptitudinilor (20 min)
Locația geometrică a punctelor (HMT) este un set de puncte care posedă anumite proprietăți.
Cunoscută de GMT:
1. Mediul perpendicular pe segment este setul de puncte echidistant de la capetele segmentului.
2. Un cerc este un set de puncte echidistant de la un anumit punct - centrul unui cerc.
3. Bisectorul unghiular este un set de puncte echidistant față de laturile unghiului
· Deci, vom demonstra teorema: perpendiculara pe lungimea unei geometrice-kim puncte loc la aceeași distanță de capetele acestui segment.
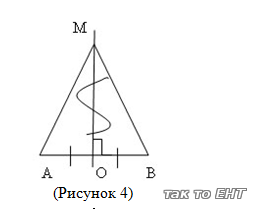
Dată: AB; MO - mijlocul perpendicular
Dovedeste: AM = BM
1. MO - mijlocul perpendicular (prin ipoteză) -> O - punctul central al segmentului AB. MO AV
2. Luați în considerare AMO și WMO - dreptunghiulare
MO - cathet comun
AO = VO (O - mid AB) -> AMO = WMO (2-m cateta) -> AM = BM (prin definiție triunghiuri egale, partea corespunzătoare)
Ce ar trebui să fie dovedit
Tema: "Dovedeste o teoremă inversă la acest lucru"
Teorema: "Fiecare punct echidistant de la capetele unui segment se află pe mijlocul perpendicular pe acest segment".
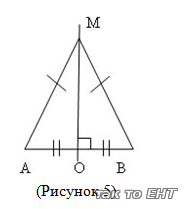
Dovedeste-o. Punctul M se află pe perpendicularul mijlociu
1. Deoarece MA = MB (prin ipoteză) -> AMB este isoscele (prin definiție).
2. Realizăm MO AV, adică omitem hAB.
3. Deoarece AB este baza unui AMB isoscel, atunci MO este o medie -> AO = OB (prin proprietatea unui triunghi isoscel).
astfel MO este mijlocul perpendicular care conține toate punctele echidistant de la capetele segmentului.
Proprietatea perpendicularilor medii pe laturile triunghiului
Se intersectează într-un punct și acest punct este centrul circumcirclei în jurul triunghiului, vom studia în clasa a opta.
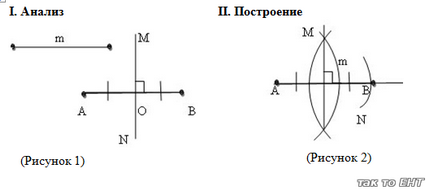
Sarcina: "Pentru a construi perpendicularul mijlociu pe segment".
· Teorema. Bisectorul unghiular este un loc geometric de puncte situate într-un unghi dat și la fel de îndepărtat de laturile sale.
· Dovada. Luați în considerare unghiul c cu vârful la punctul O și laturile a, b. Lăsați punctul C să se afle într-un unghi dat. Punem perpendicularii CA și CB din ea pe laturile a și b (figura 2). Dacă CA = CB, atunci triunghiurile dreptunghiulare AOC și BOC sunt egale (pe hypotenuse și picior). În consecință, unghiurile AOC și BOC sunt egale. Aceasta înseamnă că punctul C aparține bisectorului unghiului. În schimb, dacă punctul C aparține bisectorului unghiului, atunci triunghiurile AOC și BOC cu unghi drept sunt egale (prin hipotenuse și unghi ascuțit). Prin urmare, AC = BC. Prin urmare, punctul C este la fel de îndepărtat de laturile unui anumit unghi.
Exercițiu:
- Construiți un HMT departe de punctul O cu o distanță r.
- Construiți un GMT echidistant de la capetele segmentului AB.
- Construiți un echidistant GMT din părțile laterale ale acestui unghi.
- Construiește un HMT departe de o linie fixă l cu o distanță h.
1. Găsiți locusul centrelor de cercuri care trec prin aceste două puncte.
2. Construiți centrul cercului circumscris al triunghiului (un cerc care trece prin vârfurile triunghiului).
V. Tematica (2 minute) №231.232.233 pagina 74
VI. Rezumatul lecției (3 minute)
(oferă o evaluare calitativă a activității clasei și a studenților individuali).
Stadiul de reflecție (2 minute)