Lăsați un operator liniar

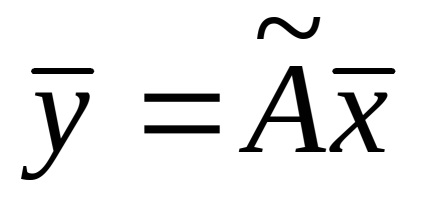
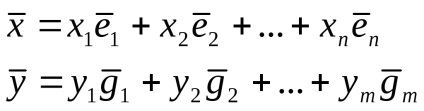
.
Ie pentru a stabili operatorul este suficient pentru a specifica doar imaginile vectorilor de bază, adică,



Să presupunem că aceste imagini au
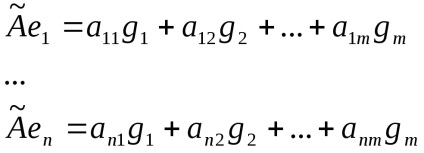
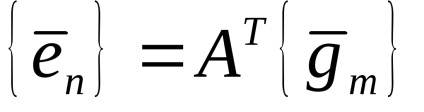

Apoi, rezultă din cele de mai sus:
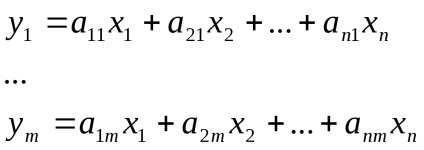
Matricea A transpune A T este o matrice a unui operator liniar, coloana k a matricei este compusă din coordonatele vectoriale

Se pare că unele dintre caracteristicile acestei matrice nu depinde de bazele și caracterizează proprietățile intrinseci ale operatorului. Deci, vom scrie fără dovada că rangul matricei unui operator liniar este egal cu dimensiunea spațiului de imagini. Vom numi acest rang - rangul unui operator liniar. Dacă această poziție este egală cu dimensiunea spațiului de L, sau dimensiunea spațiului coincide cu dimensiunea imaginilor inverse ale spațiului, operatorul

În cazul în care setul de imagini și set de imagini inverse aparțin aceluiași spațiu, vom vorbi despre transformarea spațiului în sine și operatorul operatorului de conversie va fi numită o transformare liniară sau un operator liniar. În viitor, vom lua în considerare operatori liniari și operatorii să utilizeze termenul.
Modificarea matricei operator liniar
în timpul tranziției de la o bază la alta.
Am menționat deja că matricea operatorului liniar depinde de baza. Luați în considerare problema dependenței matricei de bază, în general. Să set operatorul y =

In unele baza corespunde unei transformări liniare Y = AX.
Vom introduce o nouă bază. Dacă matricea de tranziție este T, atunci X = TX * Y = TY *.
De aceea avem TY * = ATX *; Y * = T -1 ATX *.
Sau Y * = A * X *; A * = T -1 AT.
Rețineți că matricea A și A * se spune că sunt similare (T - matricea nesingular).
Vectori și valori proprii
Nenul vector x este numit un vector propriu al unui operator liniar


Numărul nazyvaetsya numărul propriu sau eigenvalue

pentru că operator

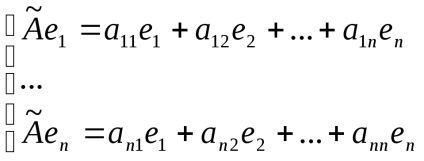
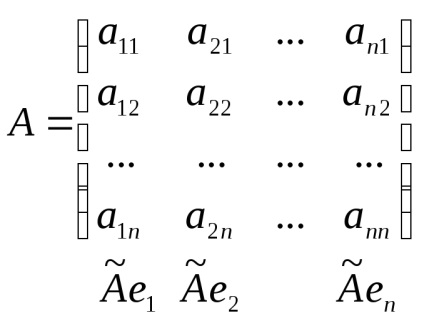
Scris sub formă de coordonate de egalitate

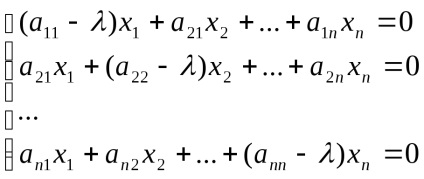
Acest sistem de ecuații liniare omogene pentru coordonata X a vectorului dorit. pentru că x 0, sistemul ar trebui să aibă o soluție non-zero. Prin urmare, în acest scop, ar trebui să fie det (A -E) = 0, sau
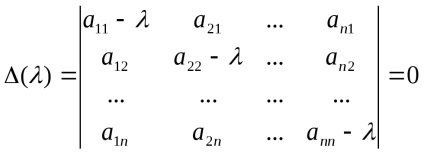
Ecuația () = 0 se numește ecuația caracteristică pentru un operator liniar

n grade relativ - polinomiale caracteristic.
Prin teorema fundamentală a algebrei, fiecare polinom de gradul n are n rădăcini cu multiplicități. Prin urmare, ecuația caracteristică are cel puțin o rădăcină, adică fiecare operator are cel puțin un vector propriu. Este adevărat în polinomul spațiul real nu poate avea rădăcini reale și, prin urmare, în spațiul nostru liniar fiecare operator liniar are vectorii proprii.
astfel pentru a determina vectorul propriu trebuie să facă polinomul caracteristic, găsi toate rădăcinile sale, care sunt valorile proprii. Apoi, aveți nevoie pentru fiecare sistem vmestov substitut eigenvalue i și găsi toate liniară sale - soluții independente. Numărul acestor soluții este n - ri. unde ri - rang al matricei A -i E. Rezultă că dimensiunea vectorilor proprii corespunzătoare propriei chislui egală cu n - ri.
Să ne amintim că matricea operatorului liniar variază cu baza:
dacă există o bază în care matricea A * ar avea o diagonală? Următoarea teoremă are: să matritsaA în baza de date ek> este diagonală, este necesar și suficient ca vektoryek de bază a avut vectorii proprii ale acestui operator.
Dovada: Să ek sunt vectorii proprii operatoraA. atunci
Prin urmare, matricea A are forma mustului
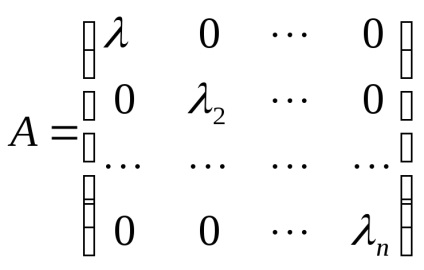
și vice-versa. Fie A - o matrice diagonală a operatorului A în baza de ek>. apoi sootnoshnniya
ia forma (*), ceea ce înseamnă că ek - vectorii proprii.
Scriem cu nici o dovada a unei proprietăți operator liniar că vectorii proprii ai unui operator liniar care corespunde diferitelor valori proprii sunt liniar independente.
Definiția. operator call. matrice este redus la forma diagonală, structura simplă a operatorului. Scriem fără dovezi, că operatorul are o structură simplă în două cazuri: 1) caracteristice imeetn polinom rădăcinile distincte; 2) pentru fiecare grad kornyai kratnostiki matricei (A -iE) a fost ravenn-ki.
Luați în considerare ceea ce este determinantul matricei unui operator liniar cu schimbarea bazei.
det (A *) = det (T -1 AT) = det (T-1) det (A) det (T) = det (A) det (T -1 T) = det (A) det (E) = det (A)
Astfel, putem concluziona că valoarea determinantului operatorului liniar nu depinde de alegerea temei. Pentru a găsi valorile proprii ale operatorului liniar am fost polinomul caracteristic
Deoarece valoarea determinantului nu depinde de alegerea temei, velichinydk sunt invariante - nu depind de baza. Se numește coeficient de pri n -1: dn-1 = a11 + a22 + ... + ann urme operatoraA și oboznachattrA (urme a urmelor).
Este ușor de a urmări relația dintre invarianții de conversie a sistemelor, ne confruntăm cu ecuațiile de transformare a suprafețelor de ordinul doi coordonate:
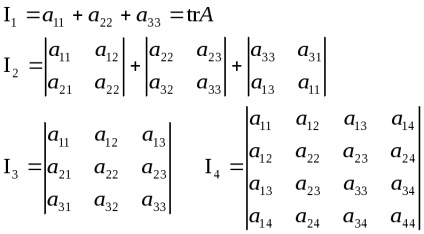
coeficienții dk și ecuația caracteristică a unui operator liniar în spațiu tridimensional. pentru N = 3. În acest sens, putem scrie formula convenabilă pentru a găsi ecuația caracteristică a unui operator liniar care acționează în spațiul tridimensional: