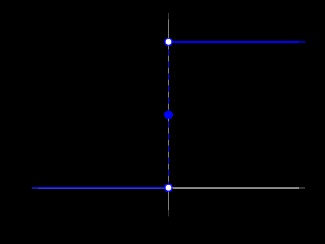
Funcția unitate Heaviside
funcția Heaviside. Funcția pas unitate. Poziția pas - funcție matematică specială. a cărei valoare este zero pentru argument negativ și unul pentru argument pozitiv:
In cele mai multe cazuri, indiferent de valoarea funcției ia zero (H (0)).
Funcția este utilizat pe scară largă în formalismul matematic al teoriei de control și de procesare a semnalului pentru a reprezenta semnale includ la un moment dat și a permis timpul rămas. Numit în onoarea lui Oliver Heaviside.
Funcția pas Heaviside este o funcție primitivă pentru funcția delta Dirac. H „= δ. ea poate fi de asemenea scrisă ca:
Cu toate că această expresie nu este matematic precis.
formă discretă
Puteți defini o funcție discretă Heaviside ca o funcție de discret argument n:
singur impuls discret Prima diferență este discret funcția Heaviside:
formă analitică
Pentru o utilizare mai convenabilă a funcției Heaviside poate fi aproximată printr-o funcție continuă:
unde k corespunde unei pante mai abrupte a funcției x = 0. Dacă presupunem H (0) = 1/2 ecuație poate fi scrisă sub forma unei limite:
Acesta este adesea folosit și este forma integrală utilă o singură funcție:
Valoarea funcției la origine poate fi administrat ca H (0) = 0. H (0) = 1/2 sau H (0) = 1. H (0) = 1/2 - cel mai frecvent caz, în vederea creșterii simetriei și legătura sa cu funcția de conectare:
Valoarea la originea poate fi indicată în mod explicit în funcțiile de înregistrare:
Există mai multe alte aproximări ale funcțiilor continue:
transformata Fourier
Este dovedit faptul că derivata funcției Heaviside este o funcție delta. Aceasta este funcția Heaviside - o funcție de delta primitivă:
.
Prin urmare, prin aplicarea unei transformări Fourier la o funcție de delta primitivă, vom obține imaginea de felul ei:
(Al doilea termen - care corespunde frecvenței zero în expansiune - descrie DC offset a funcției Heaviside sus; să fie transformat funcția nui fără ea).
Vezi ce „funcția Heaviside individuală“ în alte dicționare:
Funcția Heaviside - Funcția unică funcția Heaviside Heaviside (o singură funcție pas, pas unitate funcțională, unitate inclus) funcția constantă egală cu porțiuni zero, pentru valori negative ale argumentului, și unul pentru podea ... Wikipedia
unitate Heaviside - o funcție de unitate funcțională Heaviside Heaviside funcția de unitate pas, poziția pas al unei funcții matematice speciale a căror valoare este zero pentru argument negativ și unul pentru argumente pozitive ... Wikipedia
Funcția Dirac - funcția δ (sau funcție delta, δ funcția Dirac, Dirac delta impuls Funcția unitate) permite înregistrarea densitatea spațială a cantității fizice (masa, taxa, intensitatea sursei de căldură, forța, etc ...) Sau concentrate ... ... Wikipedia
Funcția Delta - În acest termen, există alte utilizări, vezi Delta (dezambiguizare) .. O diagramă a funcției delta unidimensionale. Funcția Delta (sau ... Wikipedia
Δ-funcție - (sau funcție delta, δ funcția Dirac, Dirac delta impuls Unitatea funcție) permite înregistrarea densitatea spațială a cantității fizice (masa, taxa, intensitatea sursei de căldură, forța, etc ...) Sau concentrat ... ... Wikipedia
Funcția Dirac delta - δ funcție (sau funcție delta, δ funcția Dirac, Dirac Unitate delta funcție de impuls) permite înregistrarea densitatea spațială a cantității fizice (masa, taxa, intensitatea sursei de căldură, forța, etc ...), concentrate sau ... ... Wikipedia
Funcția Delta - funcția δ (sau funcție de delta, δ funcția Dirac, Dirac delta impuls Funcția unitate) permite să înregistreze densitatea spațială a cantității fizice (masa, taxa, intensitatea sursei de căldură, forța, etc ...) Sau concentrate ... ... Wikipedia
Funcția Puls - funcția δ (sau funcție de delta, δ funcția Dirac, Dirac delta impuls unitate funcțională) permite să înregistreze densitatea spațială a cantității fizice (masa, taxa, intensitatea sursei de căldură, forța, etc ...) Sau concentrat ... ... Wikipedia
Laplace transforma - Laplace transforma integral funcția de conectare de transformare a unei variabile complexe (imagine) cu funcția unei variabile reale (original). Cu aceasta, vom studia proprietățile sistemelor dinamice și ezitantă ... ... Wikipedia
Laplace transforma - Laplace transforma integral funcția de conectare de transformare a unei variabile complexe (imagine) cu funcția unei variabile reale (original). Cu aceasta, vom studia proprietățile sistemelor dinamice și pentru a rezolva diferențiale și ... Wikipedia