Sarcină. Punctul A (2,1), B (1, -2), C (1,0) sunt vârfurile triunghiului ABC.
a) Găsiți ecuația triunghiului laturile ABC.
b) Găsiți ecuația unuia dintre medianele triunghiului ABC.
c) Găsiți ecuația unui triunghi ABC înălțimi.
d) Găsiți ecuația unuia dintre Bisectoarele triunghiului ABC.
d) Găsiți zona triunghiului ABC.
Soluția se realizează cu ajutorul unui calculator.
coordonatele date ale triunghiului: A (2,1), B (1, -2), C (-1,0).
1) Coordonatele vectorilor
Coordonatele vectorilor este dată de:
X = xj - xi; Y = yj - yi
Aici coordonatele X, Y a vectorului; xi. yi - coordonatele punctului Ai; xj. yj - coordonatele punctului Aj
De exemplu, pentru vectorul AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB (-1; -3)
AC (-3; -1)
BC (-2; 2)
2) Modulele vectorilor
Lungimea vectorului A (X, Y), exprimat în termeni de coordonatele sale prin formula:
3) Unghiul dintre drepte
Unghiul dintre vectorii a1 (X1, Y1), a2 (X2, Y2) poate fi găsită prin formula:
unde a1 a2 = X1 X2 + Y1 Y2
Am găsit unghiul dintre laturile AB și AC
# 947; = Arccos (0,6) = 53,13 0
4) Proiecția vectorului
Proiecția vectorului b unui vector poate fi găsit folosind formula:
Noi găsim proiecția vectorului AB pe vectorul AC
5) Suprafața unui triunghi
Să punctul A1 (x1, y1), A2 (x2; y2), A3 (x3, y3) - nodurile ale triunghiului, în timp ce suprafața sa este exprimată prin formula:
Pe partea dreaptă este determinant de ordinul al doilea. Zona unui triunghi este întotdeauna pozitiv.
Decizie. Luând A pentru primul summit, găsim:
Conform formulei obținem:
6) Divizarea segment în acest sens
Vectorul raza punctelor r A, împarte segmentul AB în relație AA: AB = m1: m2. definită prin formula:
Coordonatele punctului A este dat de:
triunghi ecuație median
Notăm punctul central al BC litere M. Apoi coordonatele punctului M vor găsi formule de împărțire în două a segmentului.
M (0, -1)
Ecuația AM mediana găsi, folosind formula pentru ecuația de o linie dreaptă care trece prin cele două puncte specificate. AM mediana trece prin punctele A (2, 1) și M (0, -1), astfel încât:
sau
sau
y = x -1 sau y -x +1 = 0
7) Ecuația liniei
Linia dreaptă care trece prin A1 (x1, y1) și punctul A2 (x2, y2), reprezentat de ecuațiile:
Ecuația liniei AB
sau
sau
y = 3x -5 sau y -3x +5 = 0
Ecuația liniei de curent alternativ
sau
sau
y = 1/3 x + 1/3 sau 3y -x - 1 = 0
Ecuația liniei BC
sau
sau
y = -x -1 și y + x + 1 = 0
8) înălțime Lungimea triunghi trasată de la punctul A
Distanța d de la punctul M1 (x1, y1) la linia Ax + By + C = 0 este egală cu mărimea valorii absolute:
Gasim distanța dintre punctul A (2, 1) și linia BC (y + x + 1 = 0)
9) înălțimea ecuației vertex C
O linie care trece prin punctul M0 (x0, y0) și perpendicular pe linia Ax + By + C = 0 are un vector direcțional (A, B), și deci reprezentat de ecuațiile:
Această ecuație poate fi găsit într-un alt mod. Pentru a găsi această linie unghiulară coeficient k1 AB.
Ecuația AB: y = 3x -5, adică k1 = 3
Vom găsi panta k perpendicularei de la starea de perpendicularitate a două linii drepte: k1 * k = -1.
Substituind acest k1 coeficient unghiular directe obținut.
3k = -1, unde k = -1/3
Deoarece perpendiculara trece prin punctul C (1,0) și are k = -1 / 3 se va căuta ecuația în forma: y-y0 = k (x-x0).
Introducerea x0 = -1, k = -1/3. y0 = 0, obținem:
y-0 = -1/3 (x - (- 1))
sau
y = -1/3 x - 1/3
Ecuația bisectoarei triunghiului
Găsim bisectoarea unghiului A. Punctul de intersecție al bisectoarea cu latura BC denota M.
Noi folosim formula:
Ecuația AB: y -3x +5 = 0, ecuația AC: 3y -x - 1 = 0
^ A ≈ 53 0
Se împarte în jumătatea unghiului bisectoarea, prin urmare, unghiul de NAK ≈ 26,5 0
Tangenta unghiului de înclinare AB este 3 (deoarece y -3x +5 = 0). Unghiul de înclinare este de 72
^ NKA≈ 180 0-72 0 108 0 =
^ ANK ≈ 180 0 - (+ 108 0 26,5 0) ≈ 45,5 0
tg (45,5 0) = 1
Bisector se extinde prin punctul A (2,1), utilizând formula, avem:
y - y0 = k (x - x0)
y - 1 = 1 (x - 2)
sau
y = x -1
Descărcați: xml
Exemplu. Sunt coordonatele vârfurile triunghiului ABC: A (-3, -1), B (4, 6) C (8; -2).
Necesar: 1) pentru a calcula lungimea laturii BC; 2) Găsiți ecuația BC lateral; 3) Găsiți triunghiul interior unghiul la vârf B; 4) echivala înălțimea AK trasată de la punctul A; 5) caută coordonatele omogene ale centrului de greutate al triunghiului (punctul de intersecție al medianelor); 6) Pentru a face desenul unui sistem de coordonate.
- echivala mediana trasată de la punctul B, și se calculează lungimea.
- echivala înălțimea trasată de la punctul A, și se calculează lungimea sa.
- Găsiți cosinusul unghiului triunghiului intern B ABC.
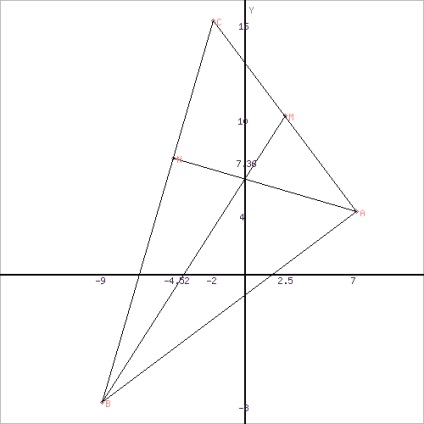
Exemplul №3. vertex Dată A (1, 1), B (7, 4), C (4, 5) a triunghiului. Găsiți: 1) lungimea laturii AB; 2) Unghiul intern A, în radiani la 0,001. Asigurați-desen.
descărcare
EXEMPLUL №4. vertex Dată A (1, 1), B (7, 4), C (4, 5) a triunghiului. Găsiți: 1) înălțimea ecuației tras prin vertex C; 2) ecuația median tras prin vertex C; 3) Punctul de intersecție al înălțimi de triunghi; 4) lungimea altitudinii trase din vârful C. Asigurați desen.
descărcare
EXEMPLUL №5. Sunt vârfuri ale triunghiului ABC: A (-5, 0), B (7; -9), C (11; 13). Definiți: 1) lungimea laturii AB; 2) laturile ecuație AB și AC, și coeficienții lor unghiulare; 3) Aria unui triunghi.
Decizie.
Coordonatele vectorilor este dată de:
X = xj - xi; Y = yj - yi
Aici coordonatele X, Y a vectorului; xi. yi - coordonatele punctului Ai; xj. yj - coordonatele punctului Aj
De exemplu, pentru vectorul AB
X = x2 - x1; Y = y2 - y1
X = 7 - (- 5) = 12; Y = -9-0 = -9
AB (12; -9), AC (16; 13), BC (4; 22).
Lungimea laturilor triunghiului
Lungimea vectorului A (X, Y), exprimat în termeni de coordonatele sale prin formula:
zonă a unui triunghi
Să punctul A1 (x1, y1), A2 (x2; y2), A3 (x3, y3) - nodurile ale triunghiului, în timp ce suprafața sa este exprimată prin formula:
Pe partea dreaptă este determinant de ordinul al doilea. Zona unui triunghi este întotdeauna pozitiv.
Decizie. Luând A pentru primul summit, găsim:
Conform formulei obținem:
Ecuația unei linii drepte
Linia dreaptă care trece prin A1 (x1, y1) și punctul A2 (x2, y2), reprezentat de ecuațiile:
Ecuația liniei AB
Ecuația Canonical a liniei:
sau
sau
y = -3/4 x -15/4 sau 4y + 3x = 0 +15
Linia pantă AB este egal cu k = -3/4
Ecuația liniei de curent alternativ
sau
sau
y = 13/16 x + 65/16 sau 16y -13x - 65 = 0
Linia pantă AB este egal cu k = 13/16