\ (\ Blacktriangleright \) unghiul diedru - unghiul format de două jumătăți de avioane și \ drepte (a \). care este limita lor comună.
\ (\ Blacktriangleright \) pentru a găsi unghiul dintre planurile \ (\ xi \) și \ (\ pi \). pentru a găsi unghiul liniar (cu acută sau directă) unghiul diedru format de planurile \ (\ xi \) și \ (\ pi \):
Pasul 1: Să \ (linia de intersecție) (\ xi \ cap \ pi = a \). Planul \ (\ xi \) nota punctul \ arbitrar (F \) și trage \ (FA \ făptașul a \);
Etapa 2: Egal \ (FG \ făptașul \ pi \);
Etapa 3: TTP (\ (FG \) - perpendicularei \ (FA \) -naklonnaya, \ (AG \) - proiecție), avem: \ (AG \ făptașul a \);
Etapa 4: Unghi \ (\ unghiul FAG \) este numit un unghi diedru liniar, format planele \ (\ xi \) și \ (\ pi \).
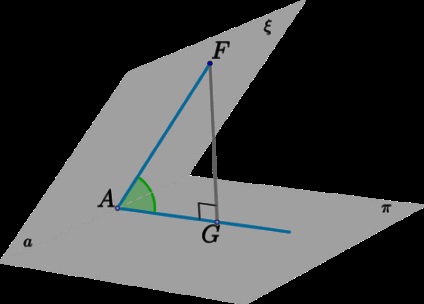
Rețineți că triunghiul \ (AG \) - dreptunghiular.
Rețineți, de asemenea, că planul \ (AFG \). astfel, este construit perpendicular pe ambele planuri \ (\ xi \) și \ (\ pi \). Prin urmare, se poate spune într-un alt mod: unghiul dintre planele \ (\ xi \) și \ (\ pi \) - unghiul dintre două linii intersectate \ (c \ în \ xi \) și \ (b \ în \ pi \) . formând un plan perpendicular pe și \ (\ xi \). și \ (\ pi \).
Să \ (SABCD \) - această piramidă (\ (S \) - apex), ale cărei margini sunt \ (un \). Prin urmare, toate fețele laterale sunt triunghiuri echilaterale egale. Am găsit unghiul dintre fețele \ (DAU \) și \ (SCD \).
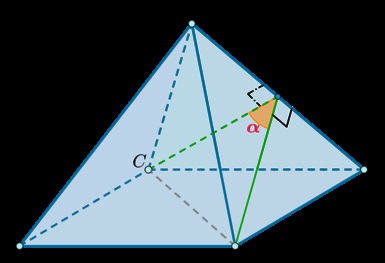
Egal \ (CH \ făptașul SD \). Deoarece \ (\ triunghi SAD = \ triunghi SCD \). de \ (AH \) va fi, de asemenea ridicat \ (\ triunghi DAU \). În consecință, prin definiție \ (\ unghiul AHC = \ alpha \) - unghiul diedru liniar între fețele de \ (\ SAD) și \ (SCD \).
Deoarece baza este pătrat apoi \ (AC = o \ sqrt2 \). Rețineți, de asemenea că \ (CH = AH \) - înălțimea unui triunghi echilateral cu laturile \ (a \). astfel \ (CH = AH = \ frac2a \).
Apoi, prin teorema lui cosinus \ (\ triunghi AHC \). \ [\ Cos \ alpha = \ dfrac = -. \ Dfrac13 \ quad \ rightarrow \ quad 6 \ cos \ alpha = -2 \]
Plane \ (\ pi_1 \) și \ (\ pi_2 \) se intersectează într-un unghi al cărui cosinus este egal cu \ (0.2 \). Plane \ (\ pi_2 \) și \ (\ pi_3 \) se intersectează în unghiuri drepte, linia de intersecție a avioanelor \ (\ pi_1 \) și \ (\ pi_2 \), paralel cu linia de intersecție a planelor \ (\ pi_2 \) și \ (\ pi_3 \). Găsiți sinusul unghiului dintre planurile \ (\ pi_1 \) și \ (\ pi_3 \).
Adauga la Favorite loc de muncă
Lăsați intersecția \ (\ pi_1 \) și \ (\ pi_2 \) - \ directă (a \). traversarea liniei \ (\ pi_2 \) și \ (\ pi_3 \) - \ direct (b \). și linia de intersecție a \ (\ pi_3 \) și \ (\ pi_1 \) - \ direct (c \). Deoarece \ (a \ paralel b \). la \ (c \ paralel un \ paralel b \) (teorema secțiunii de referință teoretică „Geometria în spațiul“ \ (\ rightarrow \) „Introducere în stereometrie, paralelism“).
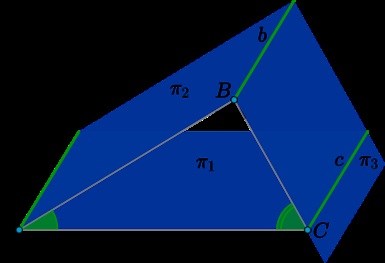
Punct Notă \ (A \ într-un, B \ în b \), astfel încât \ (AB \ făptașul a, AB \ făptașul b \) (acest lucru este posibil, deoarece \ (a \ paralel b \)). Notă \ (C \ în c \), astfel încât \ (BC \ făptașul c \). astfel \ (BC \ făptașul b \). Apoi, \ (AC \ făptașul c \) și \ (AC \ făptașul a \).
Într-adevăr, din moment ce \ (AB \ făptașul b, BC \ făptașul b \). directorul \ (b \) perpendicular pe planul \ (ABC \). Deoarece \ (c \ paralel a \ paralel b \). de \ drept (a \) și \ (c \), este, de asemenea, perpendicular pe planul \ (ABC \). și, prin urmare, orice linie a acestui plan, în special, \ directe (AC \).
Rezultă că \ (\ unghiul BAC = \ unghi (\ pi_1, \ pi_2) \). \ (\ Unghi ABC = \ unghi (\ pi_2, \ pi_3) = 90 ^ \ Circ \). \ (\ Unghi BCA = \ unghi (\ pi_3, \ pi_1) \). Se dovedește că \ (\ triunghiul ABC \) este dreptunghiular, și deci \ [\ păcat \ angle BCA = \ cos \ angle BAC = 0,2. \]
Sunt \ drept (a, b, c \). intersecting la un moment dat, unghiul dintre oricare două dintre ele este egal cu \ (60 ^ \ Circ \). Găsiți \ (\ ^ cos \ alpha \). unde \ (\ alpha \) - unghiul dintre planul format de drept \ (a \) și \ (c \). și un plan format de drept \ (b \) și \ (c \). Raspuns da grade.
Adauga la Favorite loc de muncă
Să liniile se intersectează în punctul \ (O \). Deoarece unghiul dintre oricare două dintre ele este egal cu \ (60 ^ \ Circ \). toate cele trei linii nu pot sta în același plan. Notă cu privire la linia \ (a \) litera \ (A \) și trage \ (AB \ făptașul b \) și \ (AC \ făptașul c \). Apoi \ (\ triunghi AOB = \ triunghiul AOC \) ca pătratul ipotenuzei și un unghi ascuțit. În consecință, \ (OB = OC \) și \ (AB = AC \).
Desenați \ (AH \ făptașul (BOC) \). Apoi, prin teorema trei perpendicularele \ (HC \ făptașul c \). \ (HB \ făptașul b \). Deoarece \ (AB = AC \). directorul \ (\ triunghiul AHB = \ triunghi AHC \) ca pătratul ipotenuzei și un picior. Prin urmare, \ (HB = HC \). Prin urmare, \ (OH \) - bisector \ (BOC \) (din punctul \ (H \) echidistant față de laturile unghiului).
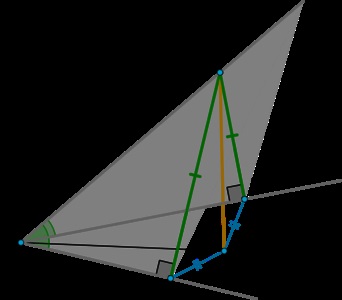
Rețineți că în acest fel am construit, de asemenea, unghiul diedru liniar format de planul format de \ drept (a \) și \ (c \). și un plan format de drept \ (b \) și \ (c \). Acest unghi \ (ACH \).
Găsim acest unghi. Deoarece punctul \ (A \), am ales la întâmplare, să am ales astfel încât \ (OA = 2 \). Apoi, în dreptunghiular \ (\ triunghiul AOC \). \ [\ Sin 60 ^ \ = Circ \ dfrac \ quad \ rightarrow \ quad AC = \ sqrt3 \ quad \ rightarrow \ quad OC = \ sqrt = 1 \.] Deoarece \ (OH \) - bisector, atunci \ (\ unghi hOC = 30 ^ \ Circ \). De aceea, într-o formă dreptunghiulară \ (\ triunghi HOC \). \ [\ Mathrm \, 30 ^ \ = Circ \ dfrac \ quad \ rightarrow \ quad HC = \ dfrac1. \] Apoi dreptunghiular \ (\ triunghi ACH \). \ [\ Cos \ unghi \ alpha = \ cos \ unghi ACH = \ dfrac = \ dfrac13 \ quad \ rightarrow \ quad \ cos ^ \ alpha = 3. \]Deoarece cele trei muchii care se extind de la un vârf al unui cub pereche, reciproc perpendiculare, marginea \ (A_1D_1 \) perpendicular pe planul feței \ (AA_1B_1B \) \ (\ rightarrow \) \ (AA_1B_1 \ făptașul A_1BC \) și \ (AA_1B_1 \ făptașul A_1KL \). atunci mărimea unghiului liniar \ (\ unghiul KA_1B \) coincide cu unghiul diedru dorit.
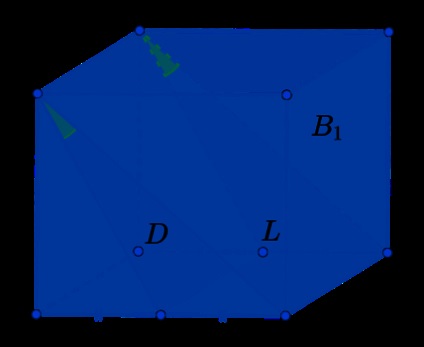
Noi luăm partea de cub \ (x \) și ia în considerare triunghiul \ (\ triunghi A_1KB \). \ (KB = \ frac \ cdot AB = \ fracx \). \ (A_1B \) - pătrat diagonal \ (\ rightarrow \) \ (A_1B = \ sqrt2x \). și lateral \ (A_1K \) pot fi găsite pe teorema lui Pitagora a triunghiului \ (\ triunghi A_1AK \):
\ [A_1K ^ 2 = A_1A ^ 2 + AK ^ 2 = A_1A ^ 2 + (\ frac) ^ 2 = x ^ 2 + \ frac = \ frac \ \ rightarrow \ A_1K = \ frac. \]
Știind toate cele trei laturi în triunghiul \ (\ triunghi A_1KB \). Puteți utiliza teorema lui cosinus pentru a găsi cosinusul unghiului dorit:
\ (KB ^ 2 = A_1K ^ 2 + A_1B ^ 2 - 2 \ cdot A_1K \ cdot A_1B \ cdot \ cos \ unghi KA_1B \) \ (\ rightarrow \)
\ (\ Frac = \ frac + 2x ^ 2 - 2 \ cdot \ frac \ cdot \ sqrt2x \ cdot \ cos \ unghi KA_1B \) \ (\ rightarrow \)
\ (\ Cos \ unghi KA_1B = \ frac> \) \ (\ rightarrow \) \ (\ cos ^ 2 \ unghiul KA_1B = 0,9 \).
Nivelul de activitate: examen dificil
Plane \ (\ pi_1 \) și \ (\ pi_2 \) se intersectează într-o linie \ dreaptă (l \). pe care punctele \ (M \) și \ (N \). Întind \ (MA \) și \ (MB \) perpendicular pe linia \ (l \) și se află în planuri \ (\ pi_1 \) și \ (\ pi_2 \), respectiv, în cazul în care \ (MN = 15 \). \ (AN = 39 \). \ (BN = 17 \). \ (AB = 40 \). Găsiți \ (3 \ cos \ alpha \). unde \ (\ alpha \) - unghiul dintre planele \ (\ pi_1 \) și \ (\ pi_2 \).
Adauga la Favorite loc de muncă
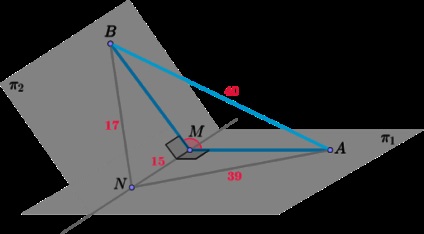
Triangle \ (AMN \) dreptunghiular \ (AN ^ 2 = AM ^ 2 + MN ^ 2 \). unde \ [AM ^ 2 ^ 2 = 39 -. ^ 2 = 15 36 ^ 2 \] Triangle \ (BMN \) dreptunghiular \ (BN ^ 2 = BM ^ 2 + MN ^ 2 \). unde \ - Noi scriem pentru triunghiul \ (AMB \) cosinus teorema [BM ^ 2 = 17 ^ 2 15 ^ 2 = 8 ^ 2 \.]: \ [AB ^ 2 = AM ^ 2 + MB ^ 2 - 2 AM \ cdot . \ cdot MB \ cdot \ cos \ unghi \] Apoi \ [40 ^ 2 = 36 ^ 2 + 8 ^ 2 AMB - \ cdot 36 \ cdot 8 \ cdot \ cos \ unghi 2 cos AMB \ prototipurilor \ leftrightarrow \ prototipurilor \ \ unghiul AMB = - \ dfrac \] Deoarece unghiul \ (\ alpha \) între planurile - este un unghi ascuțit, și \ (\ unghiul AMB \) transformat bont, apoi \ (\ cos \ alpha = \ dfrac5 \). Apoi \ [3 \ cos \ alpha = \ dfrac54 = 1,25. \]
Pregăti studenții să treacă examenul la matematică, de regulă, începe cu o repetare a formulelor de bază, inclusiv cele care permit să determine unghiul dintre planurile. În ciuda faptului că această ramură a geometriei este discutată pe larg în programa școlară, mulți absolvenți trebuie să repete materialul de bază. Știind cum să găsească unghiul dintre planurile, elevii de liceu vor putea calcula rapid răspunsul corect în cursul rezolvării problemei și se așteaptă să primească un scor decent pe baza de livrare a examenului de stat unificat.
nuanțe principale
În primul rând, trebuie să definiți linia de intersecție a planului.
Apoi, pe această linie pentru a selecta un punct și țineți-l două perpendiculare.
Următorul pas - găsirea unei funcții trigonometrică a unghiului diedru, care este format de liniile perpendiculare. Acest site este cel mai convenabil să se folosească triunghiul rezultat, din care o parte este unghiul.
Răspunsul este unghiul sau trigonometrice funcții.
Pregătirea pentru testarea examen cu „Shkolkovo“ - cheia succesului
În procesul de formare cu o zi înainte de data examenului, mulți studenți se confruntă cu problema de a găsi definiții și formule care ne permit să se calculeze unghiul dintre cele două planuri. manual școlar nu este întotdeauna la îndemână doar atunci când ai nevoie de ea. Și pentru a găsi formula potrivită și exemple de aplicare corectă a acestora, inclusiv pentru identificarea unghiul dintre planurile de Internet în modul on-line, uneori, pe care doriți să-și petreacă o mulțime de timp.
Matematică Portal „Shkolkovo“ oferă o nouă abordare a pregătirii pentru examenul de stat. Clase de la site-ul nostru va ajuta pe elevi să identifice cele mai dificile pentru el însuși și secțiuni pentru a umple golurile de cunoaștere.
Ne-am pregătit și clar stabilite toate materialele necesare. Definiții de bază și formulele prezentate în secțiunea „Teoretic Context“.
Pentru a învăța mai bine materialul, și oferă practică în punerea în aplicare a exercițiilor corespunzătoare. O mare colecție de diferite grade de complexitate a sarcinilor prezentate în secțiunea „catalog“. Toate sarcinile includ un algoritm detaliat pentru a găsi răspunsul corect. Lista de exerciții de pe site-ul este actualizat și reînnoit în mod constant.
Practicarea în sarcina în care doriți să găsiți unghiul dintre cele două planuri, elevii au posibilitatea în modul on-line pentru a salva orice loc de muncă în „Favorite“. Din acest motiv ei vor fi în măsură să se întoarcă la ea ori de câte ori este necesar și pentru a discuta despre progresul soluțiilor sale cu profesorul de școală sau de tutore.