Puteți rezolva ecuații conținând variabile folosind comenzi
rezolva și fzero.
Să examinăm mai multă soluție Matlab de ecuații neliniare, de exemplu, o ecuație pătratică x 2 - 2x - 4 = 0, introduceți următoarele:
Syms x; rezolva ( 'x ^ 2 - 2 * x -4 = 0')
Să examinăm mai multe soluții Matlab de ecuații liniare, de exemplu, aici este ecuația x - 4 = 0, introduceți următoarele:
Syms x; rezolva ( 'x -4 = 0')
Rețineți că ecuația pe care doriți să o rezolve, având în vedere ca
line, care este, luate în ghilimele simple. Răspunsul este o corectă
(Caractere) soluție 1 + rădăcină (5). Pentru soluții numerice introduceți dublu
(Ans) sau VPA (ANS), pentru a afișa mai multe caractere. Intrare rezolva echipa
poate fi, de asemenea, o expresie simbolică, dar în acest caz MATLAB programul
Se impune ca partea dreaptă a expresiei a fost închisă între paranteze, și
sintaxă rezolvarea de fapt ecuația x 2 - Sx = -7 ar arata astfel:
Syms x; rezolva (x ^ 2 - 3, * x + 7)
Răspunsul este o soluție de curent (caractere) de (3 + root (19i)) / 2
(Număr complex, unde i literă este plasată în răspunsul pentru unitatea imaginară V-1). pentru
obținerea de soluții numerice introduceți dublu (ANS), sau VPA (ANS), pentru
afișa mai multe caractere.
Utilizați rezolva comanda pentru a rezolva high-polinomul
(Polinomial) ecuație, precum și multe alte tipuri de ecuații. putea
De asemenea, rezolva ecuații care conțin mai mult de o variabilă. dacă
ecuații este mai mică decât variabila, trebuie să definiți (ca siruri de caractere), ceea ce
variabilă (e) să fie calculată. De exemplu, tipul rezolva ( '2 * x - log (y) = 1', 'y') pentru a rezolva 2x ecuație - log y = 1
y variabilă în condiții x. În mod similar, puteți specifica mai mult
una ecuație. De exemplu:
[X, y] = rezolva ( 'x ^ 2 - y = 2', 'y - 2 * x = 5')
Acest sistem de ecuații are două soluții. software-ul MATLAB oferă o soluție,
două valori ale scoate x și y valori pentru două dintre aceste soluții. Astfel,
primă soluție constă din prima valoare și prima valoare a lui x y. s-ar putea
prelua aceste valori prin introducerea liniei de comandă x (1) și y (1):
A doua soluție poate fi extrasă prin tastarea x (2) și (2).
Vă rugăm să rețineți că am numit o concluzie în comanda anterioară pentru a rezolva
formă vectorială [x, y]. Dacă utilizați rezolva sistemul de comandă
ecuații fără a se specifica ieșire în formă de vector, în acest caz, software-ul MATLAB nu
afișa automat valorile soluției:
sol = rezolva ( 'x ^ 2 - y = 2', 'y - 2 * x = 5')
sol =
x: [2x1 sym]
la: [2x1 sym]
Pentru a vedea vectorii x și valorile y și introduceți sol.x sol.u. pentru a vedea
Valorile individuale intra sol.h (1) și sol.u (1), etc.
- În acest exemplu, comanda de ieșire rezultat rezolva reprezintă o matrice structurală. Pentru a explora mai mult pe deplin această clasă de date
Unele ecuații pot fi rezolvate în mod simbolic, și în astfel de cazuri echipa
rezolva încercarea de a găsi un răspuns numeric. De exemplu:
rezolva ( 'sin (x) = 2 - x')
Uneori este mai mult de o soluție, și nu se poate obține că
se așteaptă, cum ar fi:
rezolva ( 'exp (-x) = sin (x)')
Răspunsul este un număr complex. Deși este corect
soluție a ecuației, există și soluțiile prezentate
numere reale. Grafice Funcții exp (-x) și sin (x), prezentate în Fig. 2.3;
fiecare punct de intersecție a celor două curbe reprezintă soluția ecuației e -x = sin (x).
Puteți găsi soluții numeric (aproximativ), așa cum se arată în
grafica, folosind echipa fzero care este în căutarea pentru o valoare zero a
funcție într-o valoare predeterminată x. Soluția ecuației e -x = sin (x)
zero, în funcție de e -x - sin (x), prin urmare, pentru a găsi o aproximativă
soluție la x = 0.5, introduceți următoarele:
h = @ (x) exp (-x) - sin (x);
fzero (h, 0,5)
Înlocuiți valoarea de 0,5 până la 3, și localizați următoarea hotărâre, și așa mai departe.
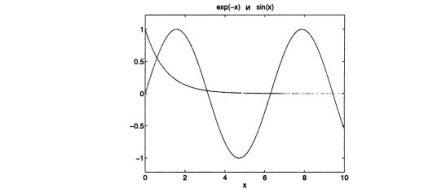
Fig. 2.3. Două curbe intersectate
← Numere complexe anterioare în Matlab
Variabile și Cesiunea Matlab Următoarea →