Soluția de ecuații în Excel Kramer și matricea inversă
Calculati valorile rădăcinilor ecuații formate prin două metode: matricea inversă și metoda lui Cramer.
Introducerea valorilor date în celula A2: C4 - matricea A și D2 celula: D4 - V. matrice
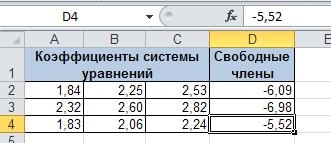
Sistemul de ecuații ale metodei matricei inverse
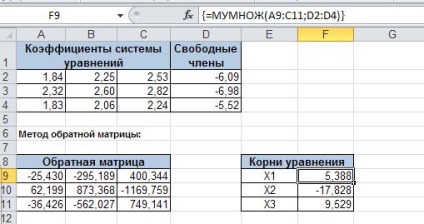
Gasim inversul matricei A. În acest scop introducem celula formula A9 = ASI (A2: C4). Apoi selectați gama A9: C11, deoarece având formula celulară. Apăsați F2, apoi apăsați CTRL + SHIFT + ENTER. Formula introdusă ca o formulă matrice. ASI = (A2: C4).
Am găsit produsul matricea A-1 * b. F9 celulei: F11 introduce formula: = MMULT (A9: C11; D2: D4) ca o formulă matrice. Ia în celule F9: rădăcinile F11:
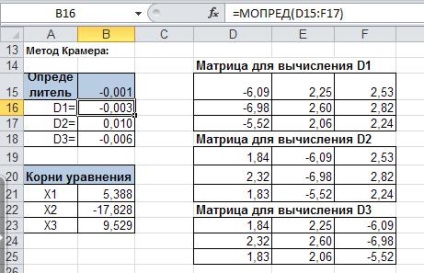
Soluția ecuațiilor de Cramer
Rezolvăm sistemul de Cramer, pentru aceasta vom găsi determinantul unei matrice.
Am găsit determinanții matrici obținute prin înlocuirea pe o coloană în coloana b.
In celula B16 intra formula = MDETERM (D15: F17),
In celula B17 intra formula = MDETERM (D19: F21).
In celula B18 intra formula = MDETERM (D23: F25).
Noi găsim rădăcinile ecuației pentru ea în B21 celule introducem: = B16 / $ B $ 15 în celula B22, introduceți: = = B17 / $ B $ 15 în B23 celulă introducem: == B18 / $ B $ 15.
Obținem rădăcinile ecuației: