În general, problema de programare liniară este înregistrată astfel încât restricțiile sunt la fel de ecuații și inegalități, iar variabilele pot fi atât non-negative și arbitrar în schimbare. În cazul în care toate constrângerile sunt ecuații și toate variabilele satisfac non-negativitate, problema de programare liniară este numit canonic. Acesta poate fi reprezentat într-o coordonată, o formă vectorială sau matrice.
1. Problema canonică de programare liniară într-o notație de coordonate are forma
.
Într-o formă mai compactă, această problemă poate fi scris folosind semnul însumare,
2. Problema canonică programării liniare în notație vector are forma
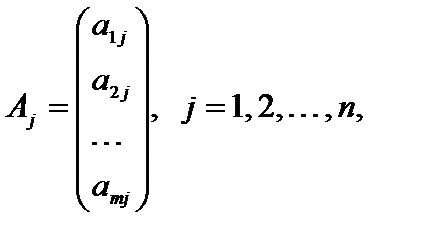
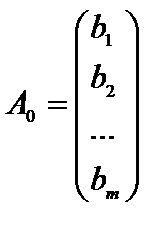
3. Problema canonică programării liniare în notație matrice are forma
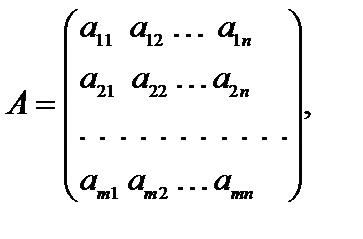
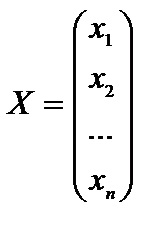
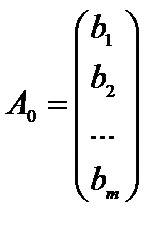
Aici, A - matricea coeficienților ecuațiilor, X - matricea coloană problemă variabilă, - o matrice coloană de laturi drepte sistem de restricție.
utilizat adesea o problemă de programare liniară, numită simetrică. care au forma de notație matrice
1.4. Reducerea problema generală a programării liniare
la forma canonică
Cele mai multe metode de rezolvare a problemelor de programare lineară se presupune că sistemul de restricție constă în ecuații și condițiile naturale de non-negativitate variabilelor. Cu toate acestea, în pregătirea modelelor matematice ale problemelor economice restricții sunt formate în principal în sistemul de inegalități, astfel încât trebuie să fie capabil să se deplaseze de la un sistem de inegalități la sistemul de ecuații. În acest scop, vom demonstra teorema următoare.
Teorema 1.1. Pentru a înlocui ecuația inegalității. Fiecare inegalitate de decizie
Aceasta corespunde unei soluții unice
și, invers, fiecare soluție a ecuației (1.13) și inegalitatea (1.14) corespunde soluției unice de (1.12).
Dovada. Să - soluția (1.12), atunci. Notăm diferența dintre dreaptă și stângă ale acestei inegalități prin intermediul. t. e.
.
Evident. Substituind în ecuația (1.13) în locul valorilor variabile. obținem
.
Astfel, satisface ecuația (1.13) și inegalitatea (1.14). Deci, prima parte a demonstrației teoremei.
Acum, să presupunem că satisface (1.13) și inegalitatea (1,14), t. E. Have
Îndepărtând partea stângă a acestei ecuații o valoare non-negativă. obține
,
t. e. satisface inegalitatea (1.12). Acest lucru dovedește teorema.
În cazul în care inegalitatea. variabila suplimentară non-negativ trebuie să fie introduse în partea stângă cu semnul minus, t. e ..
Variabilele non-negativ sunt introduse în constrângerile de inegalitate pentru a le transforma în ecuație, numite variabile complementare. variabile suplimentare sunt introduse în funcția obiectiv cu coeficienți zero, și, prin urmare, nu afectează valoarea sa.
În cazul în care problema a schimba arbitrar variabile, atunci o astfel de diferență variabilă substitut între două variabile non-negativ r. F .. în cazul în care.
Uneori trebuie să meargă în problema găsirii minime pentru determinarea și vice-versa maximă. Este suficient pentru a schimba semnele tuturor coeficienților funcției obiectiv pe partea opusă, la fel ca în restul problemei rămân neschimbate. soluții optime obținute în acest fel problemele de maxime și minime coincid, iar valorile funcției obiectiv la soluții optime diferă numai în semn.
Exemplul 1.1. Conduce la forma canonică a problemei de programare liniară.
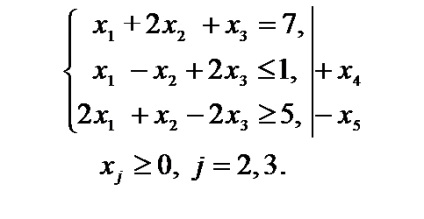
Decizie. Să ne întoarcem la problema găsirii maximă a funcției obiectiv. Pentru a face acest lucru, vom schimba semnele coeficienților funcției obiectiv. Pentru conversia ecuațiilor doua și a treia inegalitățile constrângeri ale sistemului, introducem variabile suplimentare sunt non-negative (în modelul matematic al operației este marcată cu litera E). Variabila este introdusă în partea stângă a doua inecuații cu semnul „+“, din moment ce este dat inegalitatea. Variabila este inserată în partea stângă a treia inegalitate cu semnul „-“ ca inegalitatea ia forma. Variabilele funcția obiectiv sunt introduse cu un factor egal cu zero. Variabilă. care nu este o condiție impusă de non-negativitatea se înlocuiește cu diferența. . Scrieți sarcina în forma canonică
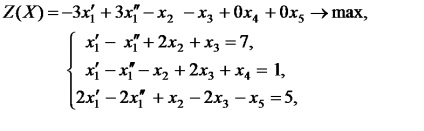
.
În unele cazuri, există necesitatea de a aduce problema la problema simetrică canonică. Să considerăm un exemplu.
Exemplul 1.2. Duce la o problemă de programare liniară formă simetrică
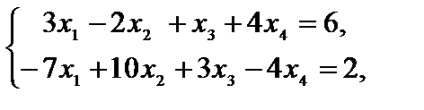
.
Decizie. Metoda Gauss-Jordan reducem sistemul de ecuații-limitate sarcini echivalente permise. În același timp, a permis necunoscut să excludă din funcția obiectiv. Pentru această problemă soluții în tabel (vezi Tabelul 1.1.) Împreună cu coeficienții sistemului constrângere de ecuații într-o linie suplimentară a scrie coeficienți de funcții obiective. Ultima coloană a liniei suplimentare (în locul partea dreapta a ecuațiilor), vom scrie termenul liber al funcției obiectiv egal cu zero. În calculele iau în considerare faptul că elementul de rezoluție în ultimul rând (funcția țintă) nu poate fi selectată.
T a b l e 1.1
Numărul -9 obținut în ultimul rând din ultima coloană a tabelului trebuie să fie scrise într-o funcție obiectiv cu semnul opus. Ca rezultat al acestor transformări, problema ia forma:
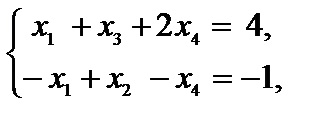
.
Deoarece variabilele sunt non-negativ, le respinge, putem scrie sarcina în formă simetrică
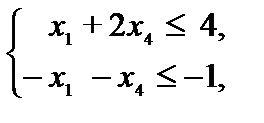
.