Metoda simplex pentru rezolvarea problemelor de programare liniară
1. Introducere. 3str
2. Metoda simplex pentru rezolvarea problemelor de programare liniară. 4-10str
3. Metoda simplex Algoritmul pentru rezolvarea problemelor de programare liniară. 11str
4. Exemplu de soluție metodei problemei simplex. 11-15str
6.Spisok folosit literatura. 17str
Lucrarea este dedicată celor mai comune metode de rezolvare a problemelor de programare liniară (metoda simplex). Metoda Simplex este metoda clasică și cea mai dezvoltată în programarea liniară. Acesta permite un număr finit de pași sau pentru a găsi o soluție optimă, sau pentru a stabili că nu există nici o soluție optimă.
Un algoritm de rezolvare a problemei, ilustrată printr-un exemplu.
1. Se specifică metoda pentru găsirea soluțiilor optime de referință
2. Se specifică metoda de tranziție de la un suport la celelalte soluții în care valoarea funcției obiectiv este aproape optim, adică, specifica modul de îmbunătățire a soluțiilor de sprijin
3. Setați criteriile care permit luarea unor decizii în timp util pentru a opri prea mult sprijin pe soluția optimă sau sledat concluzie cu privire la absența unor soluții optime.
2. Metoda simplex pentru rezolvarea problemelor liniare de programare I
Metoda simplex pentru rezolvarea problemelor liniare de programare (metoda simplex) - procedura de calcul bazat pe principiul îmbunătățirii continue a soluțiilor - tranziția de la un punct de referință la altul, pentru care funcția obiectiv pe (aceste operațiuni sunt înregistrate în tabelul simplex).
Această metodă este o metodă de sortare soluții de referință specifice ale unei probleme de programare liniară. Acesta permite un număr finit de pași sau pentru a găsi o soluție optimă, sau pentru a stabili că nu există nici o soluție optimă. Este dovedit faptul că, dacă există soluția optimă, atunci este obligat să fie găsit după un număr finit de pași (cu excepția așa-numita problemă degenerat, atunci când este posibil fenomenul de „looping“, adică revenirea la aceeași locație repetată).
Metoda Simplex este principala programare liniară. Soluția începe cu o trecere în revistă a unuia dintre vârfurile condițiilor poliedru. În cazul în care testul nu se potrivește cu vârful maxim (minim), apoi du-te la o zonă, crescând valoarea funcției obiectiv pentru rezolvarea problemei privind reducerea maximă și la rezolvarea problemei la un nivel minim. Astfel, trecerea de la un nod la altul îmbunătățește valoarea funcției obiectiv. Deoarece numărul de noduri ale poliedru este limitat, numărul finit de pași garantat pentru a găsi valoarea optimă, sau stabilirea faptului că problema este de nerezolvat.
Această metodă este universală, aplicabilă nici o problemă de programare liniară în formă canonică. Sistemul de restricții aici - un sistem de ecuații liniare, în care cantitatea necunoscute mai mare decât numărul de ecuații. În cazul în care gradul de sistem este egal cu r, atunci putem alege necunoscutele r sunt exprimate în termeni de necunoscutele rămase. Pentru definiteness, să presupunem că ați selectat primul, consecutiv, necunoscut X1, X2. Xr. Apoi, sistemul nostru de ecuații poate fi scris ca
O astfel de minte poate provoca orice sistem comun, de exemplu, prin Gauss. Nu este întotdeauna posibil să se exprime prin restul primelor necunoscutele r (am făcut-o pentru a înregistra specifice). Cu toate acestea, aceste r necunoscut trebuie să existe. Aceste necunoscute (variabile) sunt numite de bază, altele sunt gratuite.
Oferirea unor valori ale variabilelor libere și calculul valorilor baza (exprimate prin liberă), vom obține diferite soluții ale sistemului nostru de constrângeri. Astfel, puteți obține orice soluție. Suntem interesați de soluții speciale obținute în cazul în care variabilele libere sunt egale cu zero. Astfel de soluții sunt numite de bază, ele sunt la fel de mult diferite tipuri de bază de limitări în acest sistem. Soluția bazică se numește o soluție admisibilă sau soluție de referință de bază, în cazul în care este variabile non-negative. Dacă sunt luate ca variabile de bază X1, X2. Xr, soluția va fi referința cu condiția ca b1, b2. br ≥ 0.
Metoda Simplex se bazează pe teorema, care se numește teorema fundamentală a metodei simplex. Printre cele mai problema de programare liniară planuri în forma canonică este obligat să aibă o soluție de referință a sistemului său de constrângeri. Dacă problema este planul unic optim, aceasta coincide cu o soluție de referință. Diferite soluții de susținere a restricțiilor impuse de sistem număr finit. Prin urmare, soluția problemei în formă canonică ar putea căuta soluții de sprijin bust și unul dintre ei, pentru care valoarea F este cea mai mare. Dar, în primul rând, toate soluțiile de referință sunt necunoscute și trebuie să fie găsit, o, în al doilea rând, în aplicațiile reale ale acestor decizii și o mulțime de forță brută este aproape imposibil. Metoda simplex este o anumite soluții de referință enumerare procedură direcționată. Bazat pe unele găsite în avans a soluțiilor de referință printr-o anumită metodă de algoritm simplex, vom calcula noua soluție de referință, în care obiectivul valoarea funcției F este mai mică decât cel vechi. După un număr de pași ajungem la soluția de referință, care este cel mai bun plan.
Astfel, metoda simplex face o anumită ordine ca și în cazul soluțiilor de primă (sursă) de bază, precum și atunci când alte soluții de bază.
Punerea în aplicare a soluției problemei prin metoda simplex sunt ilustrate în diagrama bloc (figura 1).
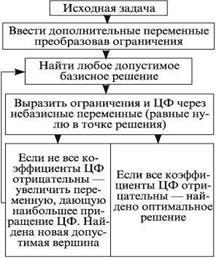
Astfel, aplicarea metodei simplex este împărțit în două etape: găsirea unui sistem fezabil de limitare soluții de bază sau constatarea inconsistența; găsirea celor mai bune soluții. In plus, fiecare etapă poate implica mai multe etape care corespund uneia sau alte soluții de bază. Dar, pe măsură ce numărul de decizii de bază sunt întotdeauna limitate, iar numărul limitat de etapele metodei simplex.
Având în vedere schema metodei simplex exprimă în mod clar natura sa algoritmică (natura unor reglementări clare privind punerea în aplicare a etape succesive), permițându-vă să programați și să pună în aplicare această metodă pe un computer cu succes. Sarcina unui număr mic de variabile și constrângeri pot fi rezolvate prin metoda simplex manual.
Vom descrie partea sa de calcul. Calculele prin metoda simplex sunt organizate sub forma unor tabele simplex, care sunt prescurtare problemă de programare liniară în formă canonică. Înainte de a elabora sarcina tabelul simplex trebuie să fie transformată, sistemul de constrângeri este redusă la o valoarea inițială acceptabilă înseamnă, c prin care funcția țintă ar trebui să fie excluse de variabile de bază. Problema acestor reforme preliminare vor fi discutate mai jos. Acum, presupunem că au făcut deja, iar problema este:
Nu este considerat a fi înregistrări specifice care ca variabile de bază pot lua X1 variabile, X2. Xr și că b1, b2. br ≥ 0 (corespunzând soluției de bază este o referință).
Pentru a compila tabelul simplex în toate egalitatea în ceea ce privește problema, care conține variabilele care sunt transferate pe partea stângă, pe partea dreapta sunt lăsate libere, și anume, Sarcina poate fi scris ca un sistem de ecuații:
Mai mult, acest sistem ia forma de tabel simplex:
Notă. Numele variabilelor de bază sunt luate doar pentru înregistrare și certitudine în tabelul reale pot fi diferite.
Lucrul cu tabelul simplex. Primul tabel simplex suferă o transformare, a cărei esență este de a trece la o nouă soluție de suport.
pentru a accesa algoritmul tabelul următor este:
vezi ultima linie (index) și tabelul coeficienților liniilor (excluzând coloana membri liber) este selectată cea mai mică valoare negativă în găsirea max, sau cea mai mare pozitivă atunci când sarcina de la min. Dacă nu există nici o este, atunci soluția inițială de bază este optimă, iar acest tabel este cel mai recent;
vizualizate coloană a tabelului care corespunde factorului negativ selectat (pozitiv) în ultima coloană cheie stroke-, iar această coloană sunt alese coeficienți pozitivi. În cazul în care nu există nici unul, funcția obiectiv este nemarginit pe valorile de toleranță ale variabilelor și problema nu are nici o soluție;
printre coloana selectată selectați coeficienții pentru care valoarea absolută a raportului membrului liber corespunzător (aflat în coloana membrilor) la elementul este minim. Acest raport se numește permisivă, iar șirul în care aceasta este o cheie;
în continuare variabila de bază linie de celule permisive corespunzătoare, care urmează să fie transferat în variabila de descărcare și fără liber elementul coloană permisiva corespunzător este introdus în numărul de bază. Construiește un nou tabel care conține noile nume de variabile de bază:
împărțiți fiecare element șir cheie (cu excepția membrilor liberi coloană) pentru un element de a permite și valorile obținute scrise în rândul cu tabelul variabil de bază modificat este nou simplex;
string rezolvarea elementului împărțit de elementul și șirul rezultat este înregistrat într-un tabel nou în aceeași poziție;
un nou tabel al tuturor elementelor coloanei cheie = 0, cu excepția înainte, este întotdeauna 1;
coloană, care are o linie de cheie 0, este aceeași în noul tabel;
line, care are o coloană cheie 0, noul tabel sunt aceleași;
rămânând în noile celule de masă stocate elemente de rezultate de conversie de masă vechi:
(Coloana de rezervă), aceasta înseamnă că se obține soluția optimă. În caz contrar, vom merge la un nou tabel simplex pentru algoritmul descris mai sus.
Metoda simplex 3.Algoritm pentru rezolvarea problemelor de programare lineară
Pentru a rezolva problema prin metoda simplex, procedați în felul următor:
1. Se aduce problema la forma canonică.
2. Găsiți soluția inițială de referință, cu o „bază unică“ (în cazul în care referința este nici o soluție problema nu are nici o soluție, având în vedere incompatibilitatea restricțiilor Adu-sistem).
3. Se calculează dilatațiile vectoriale estimate în baza soluției de referință și umple tabelul cu metoda simplex.
4. Dacă sunteți un semn de unicitatea solutiei optime, atunci soluția problemei se termină.
5. Dacă condiția existenței setului de soluții optime, prin simpla sortare sunt găsirea de soluții optime.
4. soluții Exemplu problemă metoda simplex
Aici este problema de a forma canonică.
În acest scop, în partea stîngă a primului Inegalitatea constrângeri introduc x6 variabile suplimentare cu un factor de unul. Funcția țintă x6 variabilă include un coeficient de zero (adică, nu sunt incluse).
Am găsit soluția inițială de sprijin. În acest scop, disponibilitatea (nerezolvat) egala cu zero variabile x1 = x2 = x3 = 0.
Se obține o soluție de referință de X1 = (0,0,0,24,30,6) cu o bază unitate B1 = (A4, A5, A6).
Compute estimează vectori de descompunere în baza soluțiilor de referință în conformitate cu formula:
Unde ~ Sat = (c1, c2 de la.) - vectorul coeficienților funcției obiectiv cu variabilele de bază;
Xk = (x1k, xmk x2k.) - descompunerea vectorului corespunzător în soluțiile de referință Ak vector de bază;
CK - coeficient funcție obiectiv cu XK variabilă.
Estimările vectorilor incluse în baza sunt întotdeauna zero. Soluție de referință, coeficientul de dilatare vectori și evaluare extinderi în ceea ce privește baza soluțiilor de referință sunt înregistrate în tabloul simplex
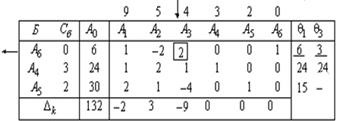
Pe partea de sus a tabelului de calcul ușor estimează coeficienții funcției obiectiv este scris. În prima coloană „B“ înregistrate vectori în baza soluțiilor de referință. Procedura de înregistrare a acestor vectori corespund numerelor permise necunoscute ecuații de constrângere. În a doua coloană, „Sat“ tabel stocate coeficienții funcției obiectiv la variabilele de bază în aceeași ordine. Cu locația corespunzătoare a coeficienților funcției obiective în „Sa“ vectorii unitate de evaluare a inclus în baza este întotdeauna egală cu zero.
Ultima linie a tabelului cu estimările # 916; k în „A0“ valorile funcției obiectiv sunt înregistrate în soluția de referință Z (X1).
Soluție de referință inițială nu este optimă, deoarece în evaluarea maximizare # 916; 1 = -2 # 916; 3 = -9 pentru vectorii A1 și A3 negativi.
Prin teorema privind îmbunătățirea soluției de sprijin, în cazul în care maximizarea cel puțin un vector are o evaluare negativă, este posibil să se găsească o nouă soluție de referință, în cadrul căreia valoarea funcției obiectiv va fi mai mare.
Definim introducerea a doi vectori conduc la o mai mare creștere a funcției obiectiv.
Incrementarea funcției obiectiv este dată de:
Se calculează valoarea parametrului # 952; 01 din prima și a treia coloană cu formula:
obține # 952; 01 = 6, cu l = 1, # 952; 03 = 3, cu l = 1 (Tabelul 1).
Am găsit incrementarea funcția obiectiv, când este introdus în primul vector de bază # 916; Z1 = - 6 * (- 2) = 12, iar al treilea vector # 916; Z3 = - 3 * (- 9) = 27.
Prin urmare, pentru o abordare mai rapidă la soluția optimă trebuie introdusă în vectorul bază de soluție de referință A3 A6 în loc de baza primului vector, deoarece opțiunea minimă # 952; 03 se realizează în primul rând (l = 1).
Jordan produc element de conversie cu X13 = 2, obținem doua X2 soluția de referință = (0,0,3,21,42,0) cu o bază B2 = (A3, A4, A5). (Tabelul 2)
Această soluție nu este optimă, deoarece vectorul A2 are o evaluare negativă # 916; 2 = - 6. Îmbunătățirea soluțiilor necesare pentru a introduce vectorul A2 în baza soluțiilor de referință.
Se determină numărul de ieșire vectorului de la linia de bază. Pentru a face acest lucru, vom calcula parametrul # 952, 02 pentru a doua coloană, este egal cu 7, cu l = 2. Prin urmare, de la terminalul de bază al doilea A4 vector de bază. Iordania pentru a produce elemente de conversie x22 = 3, se obține a treia soluție de referință X3 = (0,7,10,0,63,0) B2 = (A3, A2, A5) (tabelul 3).
Această soluție este singura optim, ca și pentru toți vectorii, baza de evaluare nepozitiv
# 916; 1 = 7/2, 916 # 4 = 2, # 916; 6 = 7/2.
Răspuns: Z max (X) = x = 201 la (0,7,10,0,63).
Soluția problemelor de programare liniară - este un proces de consumatoare de timp, mai ales atunci când un număr mare de variabile și constrângeri. Prin urmare, pentru a rezolva astfel de probleme, este recomandabil să se folosească de calculatoare. Metoda tabulară simplex este foarte potrivit pentru conturile de programare și a mașinilor.
Există implementări de software ale metodei simplex. În prezent, există sisteme integrate matematice de software pentru calcule științifice și tehnice: Eureka, PCMatLAB, MathCAD, Derive Maple V, Mathematica 2, 3. Mathematica și colab.
Cunoscut si popularitate bine-meritata a câștigat sistem de MathCad clasa de matematică dezvoltat de Mathsoft (SUA). Acestea sunt singurul sistem matematic, în care descrierea este dat probleme de matematica folosind formule matematice familiare și simboluri
6.Spisok folosit literatură
1. Ashmanov, SA Programarea liniară / S.A.Ashmanov. - M. Nauka, 1981. - 304 p.
3. Goldstein, EG Programare liniară: Teorie, Metode și aplicații / E.G.Goldshteyn, D.B.Yudin. - M. Nauka, 1969. - 736 p.
4. Kofman A. Metode și modele de operațiuni de cercetare / A.Kofman. - Mir, 1966. - 523 p.