Conceptele mulțimilor și operațiunile ne permit să rafina înțelegerea noastră a clasificării - alocarea curentă a obiectelor în clase.
Clasificarea vom face destul de des. De exemplu, numerele naturale reprezintă două clase - pare și impare. Unghiurile din planul este împărțit în trei categorii: directe, ascuțite și tăioase.
Orice clasificare este legată de partiția unui set de obiecte în subseturi. Se presupune că X este împărțit în clase X1. X2. Xn. în cazul în care:
2) combinarea subseturi X1. X2. X coincide cu X. set
În cazul în care nu sunt îndeplinite cel puțin una dintre condițiile, clasificarea este considerată necorespunzătoare. De exemplu, în cazul în care setul X subsetul de triunghiuri isoscele evidenția, triunghiuri echilaterale și versatil, pereții despărțitori noi nu ajunge ca un subset al isoscel și triunghiuri echilaterale se intersecteaza (toate triunghiuri echilaterale sunt isoscel). În acest caz, prima condiție nu este îndeplinită pe partiția claselor.
Deoarece partiția claselor asociate cu eliberarea de subseturi sale, clasificarea poate fi realizată cu ajutorul RMN-ul proprietățile elemente ale seturilor.
De exemplu, ia în considerare setul de numere naturale. Elementele sale au proprietăți diferite. Să presupunem că ne interesează numărul cu proprietatea „pentru a fi un multiplu de 3“. Această funcție vă permite să selectați dintr-un set de numere naturale un subset constând din numerele care sunt multipli de 3. Apoi,
despre celelalte numere naturale putem spune că nu sunt un multiplu de 3, adică, Obținem un alt subset al setului de numere naturale (fig. 12). Deoarece subseturi selectate sunt disjuncte și unirea lor este setul de numere naturale, atunci avem o partiție a acestui set în două clase.

În general, în cazul în care setul X este dat o singură proprietate, atunci acest set este împărțit în două clase. Prima este clasa de obiecte cu această proprietate și adăugarea a doua a primei clase la X. set In a doua clasă include o multitudine de astfel de obiecte X, care nu posedă proprietatea dată. Această clasificare se numește dihotomice.
Să considerăm acum o situație în care o multitudine de elemente pentru cele două proprietăți sunt setate. De exemplu, unele proprietăți ale numerelor naturale, ca „să fie un multiplu de 3“ și „să fie un multiplu de 5.“ Prin utilizarea acestor proprietăți ale multitudinii de N numere întregi pot distinge subseturi de jos: A - un subset de multipli de 3, și B - subset de multipli de 5. Aceste seturi sunt disjuncte, dar nici unul dintre ele este un subset al unui alt (Figura 13.).
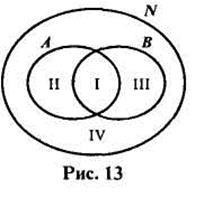
Să analizăm imaginea rezultată. Desigur, partiția setului de numere naturale în două subseturi A și B nu sa întâmplat. Dar cercul, care arată o mulțime de N, poate fi văzută ca fiind format din patru zone care nu se suprapun - acestea sunt numerotate în figură. Fiecare regiune reprezintă un subset al lui N. subset I constă din multipli de 3 și 5; subset II - de la multipli de 3 sau 5 ori; multipli III subsetul -din de 5 și nu multipli de 3; subgrup IV- de numere nu multipli de 3 sau multipli de 5. Combinația acestor patru subseturi este setul N.
Astfel, selectarea a două proprietăți au condus la partiționarea setul de numere naturale N în patru clase.
Nu ar trebui să credem că locul de muncă a celor două proprietăți ale elementelor stabilite conduc întotdeauna la partiția acestui set în patru clase. De exemplu, folosind aceste două proprietăți „să fie un multiplu de 3“ și „să fie un multiplu de 6“ set de numere naturale este împărțit în trei clase (Fig. 14):
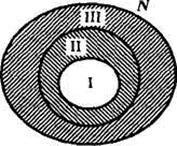
I - multipli de clasa 6; II - Clasa multipli de 3, dar nu multiplu de 6; III - numerele de clasă, fără multipli de 3.
Folosind două cifre, de exemplu, 3 și 5, se poate înregistra numere din patru cifre: 35, 53, 33 și 55. Cu toate numerele 35 și 53 sunt înregistrate cu aceleași numere, aceste numere sunt diferite. În cazul în care ordinea elementelor importante în matematică vorbesc de un set ordonat de elemente. În acest exemplu, ne-am ocupat de perechile ordonate.
Perechea ordonat format din elemente a și b, este scris de obicei folosind paranteze: (a, b). Un element numit prim coordonate (component) a perechii. și elementul b - a doua coordonate (component) a perechii.
Pereche (a, b) și (c, d) sunt egale și numai în cazul în care a = c și b = d.
Perechea ordonata (a; b) poate fi astfel încât a = b. Astfel, numerele de intrare 33 și 55 pot fi considerate ca perechi ordonate (3, 3) și (5, 5).
Perechile comandate pot fi formate ca o multitudine de elemente de una sau două seturi. Să presupunem, de exemplu, = 4, = B. Formarea unei perechi ordonate astfel încât prima componentă aparține mulțimii A și B. set vtoraya- Dacă vom enumera toate perechile, veți obține un set:
Vedem că avem două seturi A și B, am primit un set nou ale cărui elemente sunt perechi de numere ordonate. Acest set este numit produsul cartezian al seturilor A și B.
Definiția. produs cartezian seturilor A și B este mulțimea tuturor perechilor primei componente care aparține set A, iar a doua componentă aparține W. set
produs cartezian seturilor A și B reprezintă Ah V. Folosind această notație, definiția produsului cartezian poate fi scrisă ca:
PROBLEMA h și 1. Găsiți produsul cartezian de seturi A și B, în cazul în care:
Decizie. a) Se acționează conform opredeleniyu- toate perechile formează prima componentă care este selectată dintre A și celălalt - B:
b) un produs cartezian de seturi sunt egale pentru a forma toate perechile posibile de elemente ale setului:
Operația de a găsi produsul cartezian al seturilor se numește multiplicare cartezian. Să aflăm ce proprietăți această operație. Deoarece produsul cartezian A x B x A și B sunt compuse din elemente diferite, multiplicarea carteziană a A și B nu are comutativ. Putem dovedi că nu se realizează pentru multiplicarea cartezian și proprietatea asociativitate. Dar produsul cartezian este distributiv în ceea ce privește unirea și scăderea seturi, și anume, pentru orice seturi A, B și C au egalitati:
(A) x G = (A x C) (B x C)
(A \ B) x G = (A x B) \ (B x C).
PROBLEMA h și 2. Verificați valabilitatea drepturilor de proprietate distributivă multiplicare în ceea ce privește asocierea cartezian în cazul în care:
Decizie. Găsim uniunea de seturi A și B: A = B Alte elemente de listă (A) x C, utilizând definiția produsului cartezian a: (A) x C =.
Pentru a găsi elementele setului (A x C) (B x C), prima listă a elementelor mulțimilor C și A x B x C:
Vedem că setul (A B) x C, și (A x C) (B x C) constau din aceleași elemente, prin urmare, pentru seturile A date, B și C, am (A) x G = ( A x C) (B x C).
Să vedem acum cum este posibil de a vizualiza produsul cartezian de seturi.
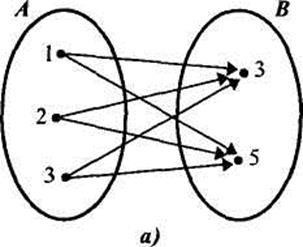
În cazul în care seturile A și B sunt finite și conțin un număr mic de elemente, poate fi reprezentat de produsul cartezian al seturilor folosind grafic sau tabel. De exemplu, produsul cartezian seturilor A = B și = poate fi reprezentată așa cum se arată în Figura 17 (a, b).
Produsul cartezian a două seturi de numerice (finit și infinit) pot fi reprezentate pe un plan de coordonate ca fiecare pereche de numere pot fi afișate în mod unic punct pe acest plan. De exemplu, produsul cartezian de mulțimi A xB = A și B = (3, 5> pe planul de coordonate va arăta așa cum se arată în figura 18.
0 1 2 3 x Fig.18
Rețineți că elementele A am arătat pe axa x, iar elementele mulțimii B - pe axa y.
Acest mod de vizualizare a produsului cartezian a două seturi de numere este utilă în cazul în care cel puțin unul dintre ei este infinit.
Problema 3. Arată pe planul de coordonate cartezian produsul Ax B în cazul în care:
R e w n e, a) Deoarece este formată din trei elemente, și setul B conține toate numerele reale de la 3 la 5, inclusiv numerele ei înșiși, atunci produsul cartezian A x B va consta dintr-un set infinit de culcușuri prima componentă care este fie 1 sau 2 sau 3, iar al doilea este orice număr real în intervalul [3, 5]. O astfel de pluralitate de perechi de numere reale pe planul de coordonate este reprezentat de cele trei segmente (Fig. 19).
0 1 2 3 x Fig. 19
b) In acest caz, fără sfârșit ambele seturi A și B. De aceea, coordonatele primei perechi aparținând setului Ax B poate fi orice număr în intervalul [1,3], și, prin urmare, punctele care reprezintă produsul cartezian al elementelor de seturi de date, A și B, formează un pătrat (Fig. 20).
z) produs cartezian R x R este format din toate numerele reale posibile. Punctele care reprezintă perechile, umple complet planul de coordonate. Astfel, produsul cartezian al R x R conține cât mai multe elemente ca puncte situate pe un plan de coordonate.
În matematică și alte științe este considerat nu numai perechile ordonate, dar, de asemenea, a ordonat seturi de trei, patru, etc. elemente. De exemplu, un număr record de 367 este un set ordonat de trei elemente, și scriind cuvântul „matematică“ - un set ordonat de 10 elemente.
Seturile comandate sunt adesea numite tupluri și variază în lungime. Lungimea tuplu - numărul de elemente din care este compus. De exemplu, (3, 6, 7) - un tuplu de lungime 3 (m, o, t, f, m, o, t, și k, a) - un tuplu de lungime 10.
Luați în considerare matematica, și produsul cartezian de trei, patru, și chiar seturi.
Definiția. produs cartezian seturilor A1. A2. A n este mulțimea tuturor secvențelor de lungime n, care aparține primului set de componente A1. în al doilea rând - A2 set. n-lea - Un set.
. Fe w elemente n e ale pluralității A1 x A2 x A3 sunt tuple de lungime 3 astfel încât prima componentă A1 aparține setului, un al doilea - set A2. Set A3 - al treilea.