B9, există o clasă de probleme în care este dat o funcție de program. Tot ceea ce este cunoscut - este o funcție a ecuației și tangenta. Și astăzi vom învăța să rezolve doar o astfel de problemă.
Rezolvam exemplu din lumea reală
Deci, prima sarcină:
Direct \ [y ~ = 16x-38 \] este tangenta la graficul funcției:
Găsiți abscisa punctului de tangență.
Mai întâi de toate, să ne amintim că o tangentă la graficul funcției. Deci, avem un program, precum și direct, care se referă la acest grafic, adică intersectează graficul numai la un moment dat, unghiul de intersecție cu axa $ Ox $, mai precis, tangenta acest unghi este egal cu valoarea derivatului în acest moment ..:
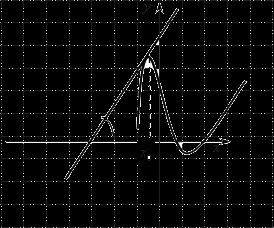
Acum, traduce definiția formală în limba care poate fi citit-uman. În primul rând, pentru că linia noastră dreaptă dată de ecuația, este o tangentă, aceste ecuații au în mod necesar un punct comun, adică. E., Ei au o soluție comună. Prin urmare, putem echivala părți dreptul lor, adică E..:
Pe de altă parte, pentru că este o tangentă grafic, mai degrabă decât o secțiune transversală arbitrară, putem solicita sunt incluse nu numai funcțiile de sine, ci și derivații lor, și anume E..:
Să luăm prima expresie:
Aici avem primul desen sau model. Această ecuație de gradul al treilea. Pentru ao rezolva, puteți încerca să se descompună polinomul în factori, și, într-adevăr, după anumite transformări și câteva linii de calcule vom obține câțiva candidați pentru răspunsul. Cu toate acestea, amintiți-vă că aceasta este o sarcină simplă a EGE în matematică, cu sarcina de a partea B. Prin urmare, ar trebui să fie rezolvate mult mai ușor, fără extinderi. Și din acest motiv ne-am dat a doua ecuație. Am asemănat deja derivați, iar acum să le conta:
Avem ecuație de gradul doi. Această identitate poate fi ușor rezolvate și prin formule discriminant si Wyeth. Să-l rezolve conform formulei vieta:
\ [\ Stânga (-3 \ dreapta) \ left (+1 \ dreapta) = 0 \]
Deci, avem două rădăcini, cei doi candidați pentru răspuns, t. E. Aceste abscisei la care derivata tangenta noastre la graficul funcției este egală cu derivatul. Acum, înapoi la designul nostru original și ne amintim că, în plus față de funcțiile ei înșiși derivați trebuie să fie de asemenea egal, adică. E. Am primit de la „X“ pentru a alege cele care satisfac ecuația. Să substitut \ [= 3 \]:
Evident, \ [= 3 \] este rădăcina ambelor expresii - și original și derivatul nostru. La această soluție ar putea încheia, dar să fiabilitate și înlocuim \ [= - 1 \]:
\ [- 1-3 \ cdot 1-9 \ cdot \ left (-1 \ dreapta) + 27 = 0 \]
Este clar că această expresie nu este egalitate. Prin urmare, \ [= - 1 \] nu este o rădăcină a identității noastre. Am tras concluzia că o singură rădăcină, care îndeplinește toate cerințele este \ [= 3 \]. Acesta este răspunsul la problema. Am găsit abscisa punctului de contact la program.
puncte cheie
În concluzie, să trecem din nou peste cheie soluțiile pași.
În primul rând, ceea ce înseamnă că linia este tangenta graficului funcției? Acest lucru înseamnă că directe și $ f \ stânga (x \ dreapta) $ au o soluție comună. Prin urmare, putem echivala $ y $ a expresiilor. Obținem prima identitate.
Cu toate acestea, după convertirea sa, obținem ecuația de gradul al treilea, și ca o astfel de structură, în general, rezolvată destul de dificil și are, de asemenea, mai multe rădăcini, înregistrăm ecuația auxiliar, amintindu-ne că vorbim despre tangenta la graficul funcției, adică. E. decât adevărat $ f \ stânga (x \ dreapta) $ ar trebui să fie egal cu altul, și derivații acestora. În acest caz, instrumentele derivate sunt considerate a fi ușor. Totalul vom obține o ecuație pătratică simplă, care este apoi rezolvat cu ușurință, și se transformă două rădăcini.
Întrebarea este: care dintre aceste rădăcini este răspunsul corect? Pentru a găsi răspunsul corect, destul de fiecare dintre aceste numere pentru a substitui în ecuația noastră, avem la început. Aici vom obține că una dintre rădăcinile suntem complet mulțumiți, iar a doua rădăcină - nu, adică, nu este cu siguranță o soluție ...
Din punctul de vedere al geometriei, următoarele situații. Să presupunem că avem aici o astfel de funcție:
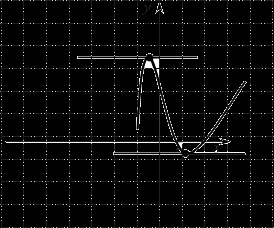
Ea are un punct maxim și un punct minim. In ambele cazuri, derivatul este zero, și, prin urmare, tangenta trasată prin fiecare dintre aceste puncte, de asemenea, are un derivat egal cu 0, adică. E. Este orizontală. Cu toate acestea, așa cum am văzut, există o tangentă la graficul functiei. În cazul în care tangenta trece din partea de sus, nu va fi capabil să traverseze curba la valoarea inferioară. Dimpotrivă, dacă luăm în considerare tangenta la cel mai jos punct, atunci acesta nu va fi capabil să traverseze curba noastră în nivelul superior. Aceasta explică faptul că, deși derivatul este un derivat al tangenta la două puncte, în cele din urmă, în ecuația noastră ne întâlnim doar una dintre ele.
- Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
