Apoi, noi spunem că punctul graficul functiei are o tangenta verticală,
dată de ecuația (1b)
1. Exemplul 1. Să funcțiile grafic sunt date două puncte. Să ne găsim ecuația:
1) linia secante care trece prin punctele
2) Ecuațiile liniilor de tangenta la graficul efectuat
Decizie. 1) Se determină panta liniei secantă ce trece prin punctele
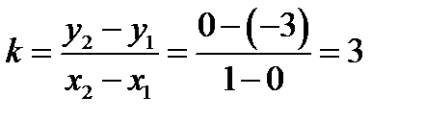
;
Folosind unghiuri de tangenta definite între graficele funcțiilor în punctul de intersecție a acestora.
Definiția 1.4. Unghiul între graficele funcțiilor în punctul de intersecție este unghiul dintre liniile tangente la acest punct Fig. 2. Acest unghi este găsit de formula
un unghi ascuțit este definit de (1.4) între
Fig.2. linii tangente.
Notă. Definiția derivatului este mai convenabil să se înregistreze și să utilizeze cu ajutorul trepte.
Definiția 1.5. Incrementele numita diferență argument și este notat cu. = Diferența este numită incrementul funcției.
Astfel, definiția derivatului poate fi rescrisă ca
Notă. Instrumentele derivate pot fi înregistrate cu următoarele simboluri
Exemplul 1.2. Folosind definiția (1.5), găsim derivatul funcțiilor într-un punct.
Decizie. Folosind definiția unui derivat (4.5), se calculează incrementul funcției în punctul. Apoi.
Folosind definiția (1.5), găsim derivata funcției.
Prin definiție, avem
Sensul fizic al derivatului. Să traseul parcurs printr-un punct în mișcare de-a lungul unei drepte, schimbarea cu timpul potrivit legii. atunci viteza medie pentru perioada de timp este definit ca;
Viteza Instantanee la momentul respectiv este (prin definiție), limita de viteză medie;