
Acasă | Despre noi | feedback-ul
În prima parte a publicației prezintă șase prelegeri privind divulgarea semnificația fizică a conceptelor și legile mecanicii de bază.
Cea de a doua parte a seriei continuă de prelegeri despre fizică și conține nouă prelegeri despre fizica moleculară și termodinamică.
Subiectul studiului fizicii moleculare este mișcarea colecții mari de molecule. În studiul folosind statistic-cer și metode termodinamice.
fizica moleculară vine de la conceptul structurii moleculare a materiei. Deoarece numărul de particule în macrosystem mari Zuko vney-dimensionale, sunt statistice, care este caracter probabilistic. Bazat pe anumite modele de fizica moleculara permite filete obyas proprietăți observabile macrosisteme (sisteme care constau dintr-un număr foarte mare de particule), deoarece efectul cumulativ al acțiunilor individuale mo-molecule. Se folosește o metodă statistică, în care ne integră acțiune resuyut nu separă moleculele, iar valorile medii ale anumitor variabile.
În utilizarea conceptului de termodinamicii și mărimi fizice prin realizarea sistemului în general, de exemplu, volum, presiune și temperatură. Termodinamica se bazează pe principii comune, sau principii, care sunt o generalizare a faptelor experimentale.
metode termodinamice și statistice pentru studierea makrosis-complementare. Metoda termodinamică ne permite să studiem fenomenul, fără cunoașterea mecanismelor lor interne. Metoda statistică este permite să se înțeleagă fenomenele stabili comportamentul de comunicare al comportamentului sistemului global și proprietățile particulelor individuale.
ATENȚIE! Publicația propusă facilitează activitatea studenților, dar nu înlocuiește TINE Lecture în public!
Teoria moleculară-cinetică (ICB)
1. Conceptul unui gaz ideal. Interpretarea cinetică moleculară a temperaturii. parametrii macroscopici ai sistemului.
2. Numărul de grade de libertate. echipartiție legii energiei. Energia interna a unui gaz ideal.
3. Presiunea gazului din punctul de vedere al teoriei cinetice moleculare a gazului ideale (ecuația de bază teoria cinetică moleculară).
4. ecuația de stare a (ecuația Mendeleev-Clapeyron) gaz ideal.
Conceptul unui gaz ideal.
Chemat gaz ideal, interacțiunea dintre moleculele este neglijabil și starea care este descrisă de Clapeyron-Mendeleev.
Modelul de gaz ideal.
1. Volumul net al moleculelor de gaz este neglijabil în comparație cu volumul vasului.
2. Între moleculele de gaz forțele de interacțiune offline.
3. Coliziunile moleculelor de gaz cu altele și cu pereții vasului absolut elastice.
Interacțiunea dintre moleculele de orice gaz devine neglijabil de slabă la densități de gaz scăzute. la vid înalt. Gaze cum ar fi aer, azot, oxigen, chiar și în condiții normale, și anume la temperatura camerei și presiunea atmosferică diferă ușor de gazul ideal. Mai ales aproape de heliu gaz ideal și hidrogen.
Nu ar trebui să credem că interacțiunea dintre moleculele unui ideal gaz existent. Dimpotrivă, moleculele sale se ciocnesc unele cu altele, iar aceste coliziuni sunt esențiale pentru stabilirea anumitor proprietăți termice ale gazului. Dar coliziuni sunt atât de rare. cele mai multe ori moleculele muta particule libere.
A fost o coliziune între moleculele vă permit să introduceți un parametru ca temperatura. Temperatura corpului caracterizează energia cu care moleculele sale sunt în mișcare. Pentru un gaz ideal în condiții de echilibru, temperatura absolută este proporțională cu energia medie a mișcării de translație a moleculelor.
Definiția. Numitul sistem macroscopic format dintr-un număr foarte mare de particule (molecule, atomi). Parametrii ce caracterizează comportamentul sistemului (de exemplu, gaz) în ansamblu este numit macroparameters. De exemplu, presiunea P. volumul V și T temperatura a gazului - macroparameters.
Parametrii care caracterizează comportamentul moleculelor individuale (viteza, masa, etc.), se numește microparameters.
Numărul de grade de libertate.
grade Opredelenie.Chislom de libertate a sistemului mecanic este numărul de variabile independente. cu care poate fi dată fiind poziția sistemului în spațiu.
a) Deoarece poziția în spațiu a punctului material este complet determinat de trei coordonatele sale (de exemplu x cartezian, y, z sau sferic. adică numărul de grade de libertate i = 3).
b) Sistemul de 2 puncte de masă asociate rigid (care le conectează segmentul este fix). Coordonatele acestor 2 puncte sunt legate. în care 5 este suficient pentru a specifica coordonatele, iar al șaselea poate fi găsit din relațiile de mai sus, și anume i = 5. În cazul în care punctele nu sunt interconectate rigid, numărul de grade de libertate i = 6. Schimbarea oferă un alt grad de libertate, care se numește oscilatorie.
sistem de reglementare alcătuit din 2 puncte asociate rigid material (sau, de exemplu, o tijă) poate fi stabilită după cum urmează: 3 set coordonate de inerție sistem și centrul C 2 al unghiului, care determină direcția axei sistemului în spațiu (Figura 7.1.).
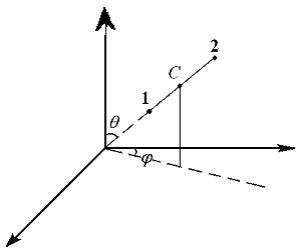
Primele trei grade de libertate se numește translație. în timp ce celelalte două - prin rotație. grade rotaționale de libertate corespunde rotației în jurul celor 2 axe perpendiculare între ele (de i = 5). c) asigurarea corp absolut rigid poate fi determinat prin specificarea coordonatelor centrului de masă 3 (grade translatie de libertate) și 3 unghi (grade de libertate de rotație). T.e.i = 6
Legea echipartiției energiei
În fizica clasică, display-uri statice Boltzmann a distribuției de energie uniformă a gradelor de libertate de molecule: pentru fiecare grad de libertate a moleculelor au o medie de aceeași energie cinetică, ravnayakT. Trebuie remarcat faptul că mișcările de translație și de rotație sunt asociate numai cu energia cinetică, în timp ce mișcarea de oscilație datorită prezenței și energiile cinetice și potențiale. în plus, valoarea medie a energiei potențiale și cinetice este același. De aceea, pentru fiecare grad de vibrație de libertate au o medie a două jumătăți de kT. Energia medie a moleculei trebuie să fie egală cu:
unde (constanta Boltzmann); aici i - suma de translație, numărul de rotație și de două ori numărul de grade de libertate de vibrație a moleculelor: