Unitatea a clădirii este bine-cunoscut pentru a vă volți. Din (3.12) vedem că B = J / C.
Deci, acum avem două caracteristici ale câmpului: putere (intensitate) și energia (potențială). Fiecare dintre ele are propriile avantaje și dezavantaje. Ce fel de răspuns este mai ușor de utilizat depinde de problema specifică.
Să presupunem că o sarcină q se deplasează într-un câmp electrostatic de la punctul 1 la punctul 2. Traiectoria taxei, ne amintim, nu este important lucru pe teren A din această cale este independentă și egală cu diferența în energia potențială a taxei de început și puncte finale:
A = W = (W 2 W 1) = W 1 W 2:
Având în vedere formula (3.11), avem:
A = q '1 q' 2 = q ( '1' 2):
Aici, „1 potențial câmp la punctul 1“ 2 câmp potențial la punctul 2. Valoarea „1“, care depinde 2. munca de teren, și se numește: diferență de potențial. Vă rugăm să rețineți că
diferența de potențial are potențialul de pornire punct minus potențial final, și nu invers!
Diferența de potențial este numită tensiune între punctele 1 și 2 și notat cu U:
Astfel, câmpul potențial la un anumit punct este munca de teren cu privire la deplasarea punctului de încărcare în potențial punctul zero, împărțit la amploarea acestei taxe.
3.4.7 Principiul superpoziției potențialelor
Luați în considerare câmpul electric creat de un sistem de n corpuri încărcate. Acest câmp poate fi privit ca o suprapunere a câmpurilor generate de fiecare organism în mod individual.
Principiul superpoziției pentru potențiale. Să rezultat un potențial de câmp la un anumit punct și "1.„2.“n potențialurilor domenii ale fiecăruia dintre organismele. apoi:
Cu alte cuvinte, potențialul câmpului rezultant egal cu suma algebrică a câmpurilor de potențiale generate de fiecare dintre organismele individual.
Principiul superpoziției pentru potențiale rezultă din (3.19), precum și faptul că activitatea forței rezultante este suma lucrării termenilor săi.
3.4.8 Câmpul uniform: stresul relație și tensiunea
Să presupunem că o sarcină q pozitivă se deplasează într-un câmp electrostatic uniform în direcția liniei de alimentare de la punctul 1 la punctul 2 (fig. 3.20). Distanța dintre punctele este d.
Această formulă este utilă pentru noi după aceea, atunci când intensitatea câmpului în condensator. Acum, să acorde o atenție la o altă consecință a formulei: unitatea de măsură este intensitatea V / m. Acest aparat este folosit mai des decât originalul H / C. Ei bine, o mulțime de lucruri a trebuit să învețe să înțeleagă că H m :-) / C = V /
3.4.9 suprafețe echipotențiale
După cum vă amintiți, introducerea de caracteristicile câmpului forței (tensiune), a făcut posibilă pentru a descrie grafic câmpul sub forma unor linii de tablouri de tensiune sau linii electrice.
Caracteristica câmpului energetic (potențială) permite, de asemenea, o imagine grafică a câmpului ca o familie de suprafete echipotentiale.
Suprafața în spațiul numit echipotențială, în cazul în care, la toate punctele de potențialul de suprafață a câmpului electric are aceeași valoare. Pe scurt, suprafața echipotențială este suprafața de potențial egal.
De exemplu, formula „= Ex vom vedea că suprafețele echipotențiale sunt toate omogene câmp plane x = const. Ele sunt perpendiculare pe liniile de tensiune. De exemplu, în Fig. 3.21 arată cinci avioane echipotențială suprafețe corespunzătoare potențialelor valori 1 «2» 3 «4 și» 5.
Fig. 3.21. suprafețe echipotențiale câmp omogen
Acum, ia în considerare a doua situația noastră standard: un câmp de o sarcină q punct> 0. Potențialul acestui domeniu, după cum am văzut, este egal cu:
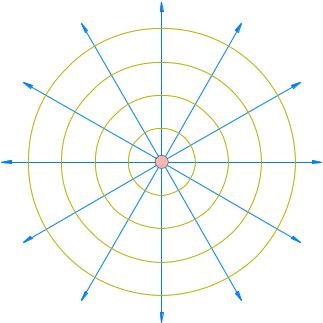
Suprafețele echipotențiale aici sunt diferite sfere r = const. Ele, de asemenea, perpendicular pe liniile de tensiune. Fig. 3.22 arată patru astfel de zone echipotențială suprafețe corespunzătoare potențialelor valori „1“ 2 „și 3“ 4.
Fig. 3.22. Punctul echipotențială suprafața câmpului de încărcare
Se pare că suprafețele echipotențiale întotdeauna perpendicular pe liniile de tensiune. Nu este greu de înțeles de ce este așa. Să presupunem că taxa se deplasează de-a lungul o suprafață echipotențială. Activitatea în acest domeniu este egal cu zero: A = q ( „1“ 2) = 0, deoarece „1 =“ 2. Prin urmare, unghiul de deplasare dintre sarcina și forța cu care acționează teren privind încărcătura, în orice moment rămâne dreaptă. Cu alte cuvinte, taxa este mutat perpendicular pe vectorul de intensitate.