Înainte de a începe algoritmi de învățare în mod direct, trebuie să aveți cunoștințe de bază despre ei înșiși grafice pentru a înțelege modul în care acestea sunt reprezentate în calculator. Nu vor fi descrise în detaliu toate aspectele legate de teoria grafurilor (acest lucru nu este necesar), ci numai cei a căror ignoranță complică în mod semnificativ absorbția acestei programare.
Câteva exemple vor da o înțelegere pic superficială a graficului. Deci, un grafic tipic este circuitul subteran, sau orice altă cale. În special, programatorul este familiar pentru o rețea de calculatoare, care este, de asemenea, un grafic. În general, există prezența punctelor conectate prin linii. Deci, pe un computer în rețea - acestea sunt servere separate, iar liniile - diferite tipuri de semnale electrice. Primul metrou - stația, al doilea - tunelurile, stabilite între ele. La punctul teoria grafurilor numite noduri (noduri) și liniile - marginile (arce). Astfel, graficul - este un set de noduri conectate de margini.
Să ne întoarcem la rețeaua de calculatoare. Are o anumită topologie, și poate fi descris în mod arbitrar ca un număr de calculatoare și modalitățile de aderare a acestora. Figura de mai jos prezintă o topologie exemplară complet conectat.
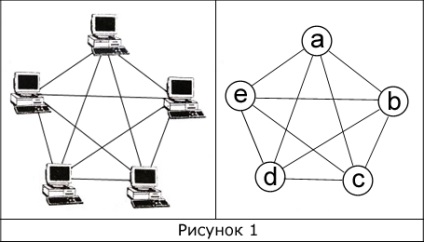
Aceasta este, în esență grafic. Cinci vârfuri sunt calculatoare, iar compusul (semnalizare cale) între ele - coaste. Înlocuiți nodurile de calculator, vom obține un obiect matematic - grafic, care are 10 muchii, și 5 noduri. Numărul nodurile pot fi într-un mod arbitrar, dar nu în mod necesar acest lucru, așa cum sa făcut în figură. Trebuie remarcat faptul că, în acest exemplu nu utilizează bucla audio, care este, o nervură, care se extinde de la vârful și imediat intră în ea, dar buclele pot apărea în sarcinile.
Iată câteva simboluri importante folosite în teoria grafurilor:
- G = (V, E), aici G - grafic, V - nodurile sale, și E - nervură;
- | V | - ordinea (numărul de vârfuri);
- | E | - dimensiunea graficului (numărul de muchii).
În cazul nostru (. Figura 1) | V | = 5 | E | = 10;
Când oricare din top orice alt vertex este disponibil, atunci acest grafic este un grafic conectat neorientat (Fig. 1). Dacă graficul este conectat, dar acest lucru nu este cazul, atunci un astfel de grafic sau digraph se numește orientat (Fig. 2).
Graficele orientate și neorientate au o noțiune de gradul de vârfuri. Gradul de vârfuri - este numărul de muchii de legare la alte noduri. Suma tuturor gradelor graficului este egală cu de două ori numărul de margini. Pentru Figura 2, suma tuturor grade este de 20.
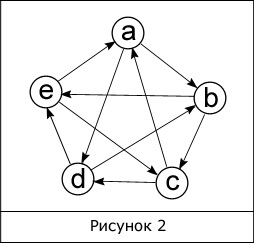
În digraph, spre deosebire de un graf neorientat, este posibil să se deplaseze de la partea de sus la partea de sus s h, fără noduri intermediare numai atunci când o nervură de ore și este inclusă în s, dar nu și invers.
grafice au forma îndreptate mai jos:
G = (V, A), unde V - topuri, A - marginile îndreptate.
Al treilea tip de grafice - graficele mixte (Fig 3.). Ei au ambele margini dirijate și nedirijate. Formal grafic mixt este scris ca: G = (V, E, A), în care fiecare dintre literele din paranteze indică, de asemenea, că au fost atribuite anterior.

Graficul din figura 3 un arc direcționat [(e, a), (e, c), (a, b), (c, a), (d, b)], altele - non-direcțional [(e, d), (e, b), (d, c) ...].
Două sau mai multe grafice de la prima vedere pot apărea diferite în structura, care se produce din cauza imagini diferite lor. Dar acest lucru nu este întotdeauna cazul. Ia două din grafic (fig. 4).
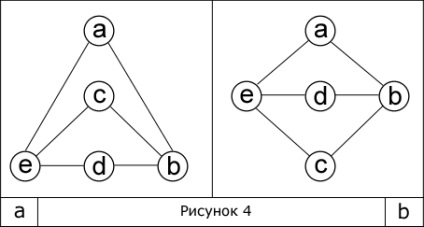
Ele sunt echivalente cu unul de altul, pentru că fără a modifica o singură structură de grafic se poate construi o alta. Aceste grafice sunt izomorfe. t. e. având proprietatea că orice nod cu un anumit număr de muchii din graful are un top identic al celuilalt. Figura 4 prezintă cele două grafice izomorfe.
Atunci când fiecare margine se atribuie o anumită valoare, numită greutatea coastelor, apoi un grafic ponderat. Diversele probleme ca și o greutate pot face diferite tipuri de măsurători, cum ar fi lungimea, preț etc. rute. N. în reprezentarea grafică a graficului indicat valori de greutate, în mod tipic în apropierea marginilor.
În oricare dintre graficele care le-am considerat că este posibil să selectați calea și cu nimeni. Cale - o secvență de noduri, fiecare dintre care este conectat la urmat de nervura. În cazul în care primul și ultimul nodurile sunt aceleași, atunci această cale se numește ciclu. Lungimea este determinată de cantitatea marginilor constituente. De exemplu, Figura 4.a este de secvență [(e), (a), (b), (c)]. Această cale este un subgraf, deoarece putem aplica definiția din urmă, și anume graful G „= (V“, E „) este un subgraf al unui graf G = (V, E), numai atunci când V“ și E „aparțin V, E .
Modalități de reprezentare grafice
Graf, la fel ca majoritatea celorlalte obiecte matematice, pot fi prezentate pe un calculator (stocat în memoria sa). Există mai multe modalități de interpretare sale, sunt cele mai faimoase dintre ele:
Folosind primele două metode implică stocarea numărarea într-un tablou bidimensional (matrice). Mai mult, dimensiunea acestor matrice va depinde de numărul de noduri și / sau margini într-o anumită coloană. Astfel, marimea matricei de adiacență n x n, unde n - numărul de noduri și matricea n incidență x m, n - numărul de noduri, m - numărul de muchii din grafic.