Dacă vom rescrie seria în ordine inversă, aceasta va fi o progresie geometrică, suma a cărei membri este
Factorul care se înmulțește cu R este notat ca sn, i. iar indicele indică durata chiriei - n, iar rata dobânzii - i. Acest factor se numește coeficientul de compoundare și reprezintă o rentă sumă anuitate acumulată, termen care este egal cu 1.
Formula (67) pot fi de asemenea folosite pentru a calcula valoarea chiriei postnumerando cu o perioadă atrasă diferită de ani. În acest caz, în loc de numărul perioadelor n substitute, și în schimb i - rata per perioadă.
2. Dobânda m ori pe an.
Aici, membrii chiria evaluate până la sfârșitul termenului de interes formează un număr (doar rescrie în ordine inversă)
unde j - rata nominală a dobânzii.
Suma termenilor progresiei geometrice este
La sfârșitul lunii în fiecare an, clientul poate pune în bancă 1 milion. Ruble. Ce sumă va fi în contul după 3 ani? i = 4%
p - RENT URGENT
1. Calcularea dobânzii o dată pe an (m = 1).
Fie p anuitate plătit o dată pe an, în cantități egale, procentul este calculat o dată pe an. În cazul în care valoarea anuală a plăților este R. de fiecare dată plătit R / p. Numărul total de membri ai anuitate egale n · p. Mai mulți membri ai acestei chirie cu interes o progresie geometrică, cu un prim element al R / p și numitorul - (1 + i) 1 / p. Suma termenilor acestei progresie
2. Calcularea dobânzii (număr de ori) coincide cu numărul de plăți pe an.
În practică, astfel de cazuri sunt destul de frecvente. În cazul în care p = m. și înlocuind în formula (67) în loc să i - j / m. și în loc de numărul de ani - numărul de perioade de plata chiriei n · p = n · m. și având în vedere că chiriile pe termen egal cu R / p = R / m obținem:
Aici avem plăți p pe an, ori m, pentru care se percepe dobândă (pm). Numărul total de membri ai anuitate egale n · p. Valoarea membru Chiriile - R / p. chiriile membri cu dobânda acumulată pe aceasta formează o progresie geometrică, cu primul membru al R / p și numitorul (1 + j / m) m / p. Cantitatea de membri ai progresiei (sau, în cazul nostru, suma rambleu)
Client timp de 5 ani de la sfârșitul fiecărui trimestru la transferurile bancare pentru 200 de ruble. Ce sumă va fi într-un cont la sfârșitul perioadei, se percepe dobanda în cazul în care: a) trimestrial; b) timp de șase luni. Rata dobanzii - 6%.
La calcularea dobânzii la jumătate get:
În consecință, atunci când schimbă cel puțin una dintre condițiile suplimentare chirie financiară redimensionată suma atrasă.
Valoarea viitoare a unei anuități ordinare, cu diferite termene de plată reprezintă S (p, m). și anume de exemplu, anuitate S (1,1) vor fi înregistrate la sfârșitul anului, dobânda percepută. și anuitate cu interes ori m un an va fi desemnat S (1, m), etc.
Să comparăm costul viitor al anuităților convenționale pentru aceeași perioadă de mărimea plăților și chiria, dar cu diferite termene de plată.
Fie n = 5, R = 1, i = 0,08 (Rata dobanzii complex):
a) pentru cazul p = 1, m = 1:
b) eslip = 1, m = 2, valoarea sumei va fi egală atrasă
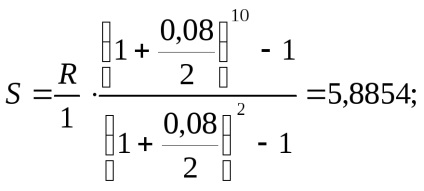
c) atunci când p = 2, m = 1, adică chiria semi-anuale de angajamente la sfârșitul anului de interes va conduce la suma cea mai mare următoare atrasă:
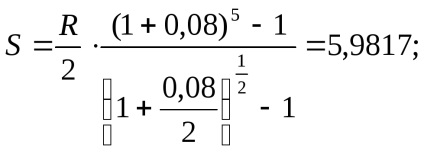
g) la egal și p m, adică, de exemplu, atunci când p = 2, m = 2:
d) în cazul în care p = 2, m = 4, adică în cazul în care chiria semi-anual cu angajamente trimestrial de interes, se obține următoarea sumă calculată:
e) pentru p = 4, m = 2:
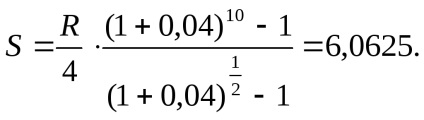
Folosind aceste inegalități pot fi presetate pentru a compara rezultatele finale ale compoundarea fluxuri de plăți, fără a recurge la calcule precise. Vom arăta acest lucru prin exemplul următor: proprietarul oferă chiriaș pe o bază lunară (la sfârșitul lunii) pentru a transfera chiria la banca în cazul în care dobânda se va percepe trimestrial (la sfârșitul trimestrului).
Chiriașul propune să utilizeze serviciile unei alte bănci, în cazul în care dobânda este calculată pe o bază lunară, dar oferă să plătească chiria trimestrial (la sfârșitul fiecărui trimestru).
Ce opțiune de plată este mai favorabilă locatorului, în cazul în care într-un an, banii vor rămâne în contul dvs.?
Noi folosim aceste inegalități pentru a compara sumele acumulate.
In primul exemplu de realizare, p = 12, m = 4, adică p> m> 1.
Într-un al doilea exemplu de realizare, p = 4, m = 12, adică, m> p> 1.
Conform cantității inegalității rambleu deasupra variantei chiriaș propuse, vor fi mai mici, S2
Aici este valoarea de calcul pentru atrasă anul (n = 1), ținând seama de faptul că chiriile anuale, în ambele cazuri este R.
Apoi, folosind formula (73), obținem:
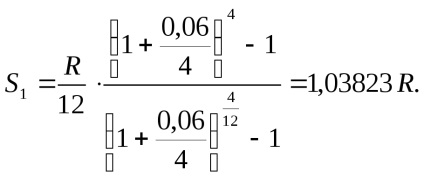
Într-o a doua variantă de realizare suma rambleu va fi egală cu:
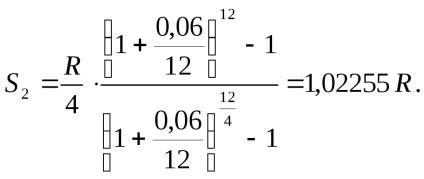
Astfel, S2
Un calcul exact nu poate răspunde doar la întrebarea de ce opțiune este preferabilă pentru proprietar, dar, de asemenea, ceea ce este suma de beneficii suplimentare. În acest exemplu, S1 și S2, diferența va fi 0,01568R sau 1,568% din chirii anuale.
Raportul de mai sus a sumelor majorate pentru diverse combinații ale condițiilor de plată și de interes sunt valabile în cazul în care rata dobânzii nu depășește 50%.
Tabel. 8 prezintă valorile sumelor atrasă pentru diferite valori ale ratei dobânzii în următoarele condiții: a) rentă anuală (p = 1), dobânda percepută de jumătate (m = 2), plățile sunt efectuate timp de cinci ani (n = 5) și R = 1; b) Semianual anuitate (p = 2), 1 la sută plătesc o dată pe an (m = 1).
Calculul se ridică la diferite atrasă de sochetaniyahmip.
Rata dobânzii i,%