în cazul în care
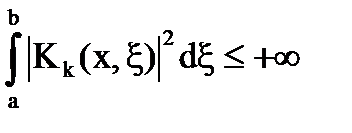
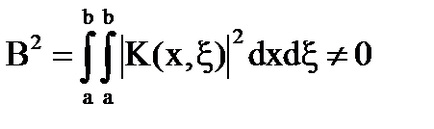
Acesta este dat de:
Deoarece seria (19) converge uniform, este posibil să se schimbe ordinea de însumare și integrare:
Notăm - seria Neumann. (23)
Această caracteristică este numită rezoluția ecuației (1). Soluția ecuației se poate scrie:
Dacă rezoluția calculată, soluția poate fi scrisă o dată ().
Definiție: Noi spunem că ecuația integrală (1) are rezoluție R (x, # 958, # 955;), în cazul în care soluția ecuației poate fi scrisă ca (24), iar această soluție este unică pentru orice termen liber f (x).
Este evident că, dacă există o rezoluție a ecuației integrale, este unic.
Într-adevăr, chiar și atunci când. ecuație are două rezoluții și. Apoi, singura soluție a ecuației poate fi scrisă ca:
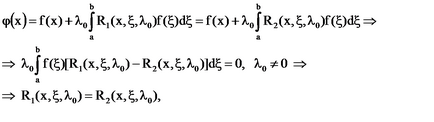
deoarece f (# 958) - o funcție arbitrară.
Notă: O rezoluție a fost definit numai pentru valori # 955;, astfel încât. Cu toate acestea, există o rezoluție a întregului planul complex # 955;, cu excepția unor valori izolate # 955;.
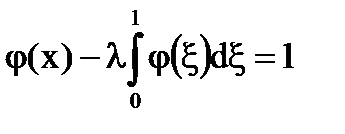
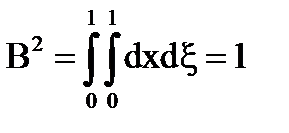
Seria Neumann converge pentru | # 955; |<1.
în mod specific # 955; ≠ 1 (în interiorul și în afara cercului | # 955; | = 1, pe cerc, cu excepția situațiilor # 955 = 1).
Notă: Pentru unele Fredholm ale seriei (23) converge pentru toți # 955;.
Să presupunem că
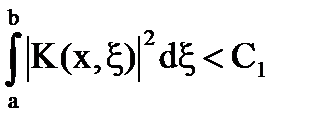
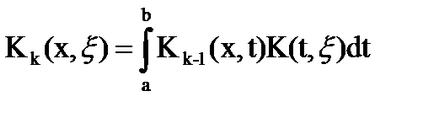
În virtutea Cauchy - Schwarz:
integrarea # 958;, obținem
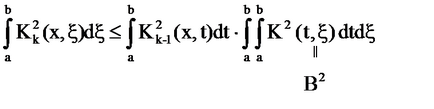
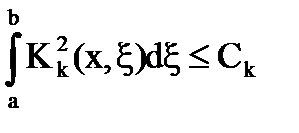
Aici. care este
Prin urmare, seria converge.
Prin urmare, rezoluția satisface următoarea ecuație integrală:
Aceasta integrala se numește «k» urme de bază sau urme -lea «k» i-lea nucleu iterated. Avem pentru x = # 958;
După integrarea x [a, b]:
Exemplu. Construi formalismul dizolvant folosind nuclee iterated.
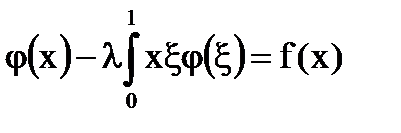
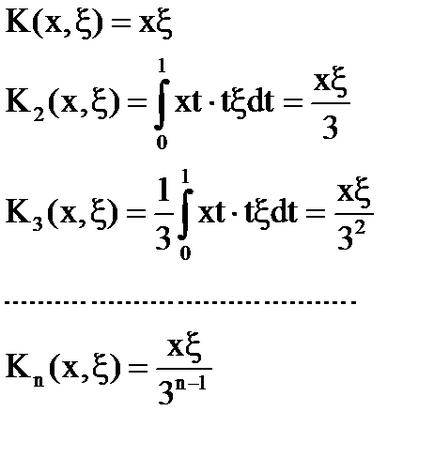
Soluția ecuației integrale:
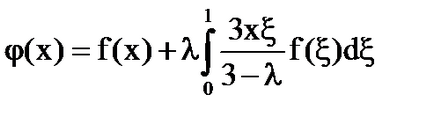
exerciţii:
Găsiți nucleul iterată pentru nucleele menționate la un definit și b
și construi o rezoluție.
Construcția de rezoluții pentru următoarele Boabele