Pentru a înțelege cum să rezolve problemele cu trapez, este util să ne amintim trei soluții de bază.
I. Pentru a efectua două înălțimi.
Ia. Cadrilaterul de BCKF - dreptunghi (ca are toate unghiurile sunt unghiuri drepte). În consecință, FK = BC.
AD = AF + FK + KD, prin urmare, AD = AF + BC + KD.
Triunghiuri ABF și DCK - dreptunghiular.
(Se va aprecia o altă opțiune:
În acest caz, AD = AF + FD = AF + FK-DK = AF + BC-DK.)
Ic. În cazul în care un trapez isoscel, soluția simplifică la
În acest caz, triunghiuri in unghi drept ABF și DCK sunt, de exemplu, un picior și un ipotenuză (AB = CD prin ipoteză, BF = CK ca înălțimea trapezoidală). Din egalitatea triunghiurilor presupune egalitatea părților în cauză:
II. Desenați o linie dreaptă paralelă cu latura.
IIa. BM ∥ CD. Deoarece BC ∥ AD (ca bază trapezoidală), apoi BCDM - paralelogram. Prin urmare, MD = BC, BM = CD, AM = AD-BC.
IIb. In particular, un trapez isoscel
BM ∥ CD. Deoarece CD = AB, atunci BM = AB. Asta este, vom obține un triunghi isoscel și un paralelogram ABM BCDM.
III. Deplasare părți și a obține un triunghi.
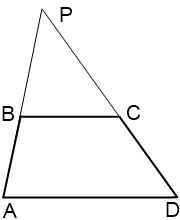
Triunghiuri și DAP sunt similare în BPC cele două colțuri (unghiul P - ansamblu, ∠ PAD = ∠ PBC ca respectiv la BC ∥ AD si secant AP).
În consecință, laturile lor sunt proporționale:
Aceste trei abordări pentru rezolvarea problemelor pe trapez - bază. Pe lângă acestea, există multe alte moduri. Unii au discutat pe acest site. De exemplu, aici - cum să rezolve problema cu trapez, care sunt perpendiculare pe diagonala.