SCOP. determinarea momentului de inerție al discului calculat și metode experimentale
ECHIPAMENTE. instalare specială, un set de greutăți, șubler, cronometru
Munca, care efectuează o forță a cuplului M atunci când corpul este rotit cu un unghi φ (în radiani)
A Mφ = (1)
De lucru forțe de frecare sau rezistență egală cu variația energiei mecanice a sistemului: A = E1 - E2 (2) Energia cinetică a masa m a corpului, care se mișcă înainte la o υ viteză și simultan se rotește cu ω viteza unghiulară în raport cu centrul de masă,
Această energie este energia cinetică a mișcării de rotație în raport cu axa instantanee (MOB):
In aceste formule, Jc - momentul de inerție față de o axă care trece prin centrul de masă, J - momentul de inerție MOB.
Dacă aceste axe sunt paralele între ele, în conformitate cu teorema lui Steiner
unde m - masa organelor, și - distanța dintre axele.
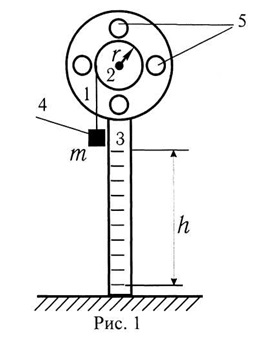
Disk 1 cu găuri filetate plantate pe axul (fig. 1) și se poate roti cu frecare redusă. Pe aceeași axă fulia 2 este r raza, care este înfășurat pe firul. La celălalt capăt al firului 4 este atașat masa m sarcină, sub care este rotit sistemul.
Calea traversat de sarcină în poziția sa cea mai mică (atunci când firul este derulată în totalitate) este determinată pe o scară de 3, de-a lungul care se deplasează de sarcină.
Găurile șuruburilor pot fi înșurubate greutăți suplimentare disc 5 de formă cilindrică (raza R) și m0 masa.
Aparatul prevede măsurarea automată a timpului de călătorie la partea de jos a încărcăturii și distanța h, care este situată pe inerția sarcină după ce trece poziție inferioară.
DESCRIERE METODA DE MĂSURARE
Dacă firul rana de pe rolă, ridicând înălțimea sarcinii m, atunci acesta va avea energie potențială, în care se încadrează de marfă, energia potențială este transformată în energie cinetică a mișcării de translație a sarcinii și energia de rotație a discului. Cunoscând timpul t de marfă toamna la punctul cel mai jos, se poate determina viteza finală a sarcinii și viteza unghiulară a discului unde r - raza rolei.
Atunci când se deplasează cuplul lagărului de frecare acționează Mtr, pentru a depăși care lucrarea este realizată în calea A = Mφ
În cazul în care unghiul de rotație a discului φ0- (deplasare unghiulară).
În conformitate cu legea conservării energiei și ecuația (2)
cuplul de frecare Mtr găsi următoarele motive. După ce sarcina va scădea la cel mai jos punct, volanta, încă coasting, ridicați sarcina la o înălțime h; există potențialul energetic MGH este mai mică decât inițială, valoarea muncii depuse împotriva forțelor de frecare în tot drumul. Din legea de conservare a energiei și cu formula (2)
Rezolvarea ecuației (7), (8), obținem formula calculată pentru momentul de inerție al corpului rotativ:
ÎNTREBĂRI toleranței
1. Care este momentul de inerție al punctului material?
2. Pe ce valori depinde de momentul de inerție al discului?
3. Care este momentul de inerție al unui corp rigid în jurul axei?
4. Unitățile de măsură momentul de inerție?
5. Care este momentul de inerție al unui sistem de corpuri în raport cu o axă?
6. Notați legea de conservare a energiei pentru sistem „drive-sarcină“.
7. La acea energie mecanică este consumat în sistem:
a) energia potențială a sarcinii atunci când aceasta este coborâtă;
b) energia cinetică a sistemului atunci când sarcina se mișcă în sus?
8. Care este poziția sarcinii corespunde cu energia cinetică maximă a volantului?
9. Prin ce formulă de lucru determinat cheltuit în depășirea forțelor de frecare?
10. Care este lucrarea momentului permanent de forță?
1. Care este metoda de determinare a momentului de inerție al unității în această lucrare? Conform unei formule se calculează în experimente?
2. Care sunt cauzele erorii în această lucrare?
3. Pe ce valori depinde de energia cinetică a unui corp la mișcarea de translație și de rotație?
4. Ceea ce caracterizează momentul de inerție al punctului material al corpului?
5. Pe ce valori depinde de momentul de inerție?
6. Statul și demonstrează teorema lui Steiner.
7. Cum se calculează momentul de inerție al unui corp solid de formă complexă?
8. Găsiți momentul de inerție al unei piramide uniformă a cărei bază este un pătrat de latură a, în raport cu o axă care trece prin vârful și centrul bazei. piramidă de masă este m.
9. Cele două puncte materiale cu mase m1 și m2 sunt conectate la rigid imponderabil lungimea tijei l. Găsiți momentul de inerție al sistemului în raport cu perpendiculara pe axa arborelui prin centrul de masă.