Există abordări diferite pentru a determina probabilitatea unui eveniment.
Una dintre aceste definiții este așa-numita definiția clasică a probabilității. Ea a apărut în faza inițială de dezvoltare a teoriei probabilității.
În această probabilitate de determinare evenimente numite număr-relație set de evenimente elementare care favorizează acest Soby-Tia, printre toate evenimentele elementare equipossible experienta.
Probabilitatea unui eveniment A este notat cu P (A). Dacă după aproximativ numărul m-medie a rezultatelor elementare favorabile evenimentului A, și n - numărul egal posibile rezultate ale experienței elementare, formând un grup complet de evenimente,
Stabilirea unor proprietăți ale probabilității unui eveniment.
Proprietatea 1. Probabilitatea unui eveniment A este un număr non-negativ între zero și unu: 0 <Р (А) <1.
Această proprietate rezultă direct din ecuația (19) Deoarece în 0 Proprietatea 2. Probabilitatea ca un anumit eveniment este egal cu unu: P (U) = 1. Acest lucru rezultă din faptul că un anumit eveniment are loc la fiecare proces (m = n). Proprietatea 3. Probabilitatea eveniment imposibil este zero: P (V) = 0. De fapt, evenimentul este imposibil pentru orice test nu trepte (m = 0). 4. Proprietate (aditiv). Dacă A și B - sunt evenimente incompatibile, probabilitatea sumei lor este egală cu suma probabilităților P (A + B) = P (A) + P (B). Exemplu. Să fie de 80 de piese, printre care 60 pot fi reparate, în timp ce 20 defect. Găsiți probabilitatea ca elementul este luată la întâmplare ochi-zhetsya intacte. Decizie. Evident, din cauza numărului de părți, adică. E. Numărul 80, 60 și nu sunt în favoarea favoarea 20. Dacă A reprezintă cazul în care elementul este în stare de funcționare luate, în conformitate cu definiția clasică-cer, probabilitatea acestui eveniment este raportul dintre numărul de elementar favorabil rezultatele la numărul de toate ravnovoz posibile. prin urmare Alte 170 de piese fabricate pe mașină, transformat piese 8 care nu îndeplinesc standardul. Găsiți probabilitatea de a selecta piese care nu respectă standardul. Controler, controlul calității produselor 500, a stabilit că 10 dintre ele aparține clasa a doua, iar celelalte - la primul. probabilitatea Naydi- de selectare a acelor elemente de clasa întâi, a doua selecție de produse de grad. La zece cărți de cifre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. scrise două dintre ele sunt scoase la întâmplare și stivuite în ordinea apariției, atunci numărul primit este citit. Găsiți probabilitatea ca numărul este impar. Șase cărți sunt scrise cu litere, d, h, o, u, x. După shove-Scoops scos la întâmplare o carte după alta și a le afișa în ordinea în care au fost luate. Găsiți probabilitatea ca cardul va fi scris cuvântul „aer“. În caseta sunt 6 roșii și 9 bile albe. Din caseta-REMOVE Misfed Cheny trei bile. Găsiți probabilitatea ca doi dintre ei vor fi roșii. Definiția clasică a probabilității implică faptul că toate rezultatele elementele-Tary sunt la fel de probabil. Despre posibilitate egala a rezultatelor-op, care de obicei încheie prin considerente de simetrie (de exemplu, ca și în cazul unei zaruri ideale sau monede). Astfel de probleme privind prac-tic rare. În multe cazuri, este dificil să se precizeze motivele pentru noi să presupunem că toate rezultatele elementare sunt la fel de probabile. În acest sens, a fost necesar să se introducă o definiție a mai probabilitate, care a devenit cunoscut sub numele de Staten-terorismului. Această definiție se bazează pe un astfel de concept ca frecvența relativă a evenimentului-TION. Definiția. Frecvența relativă a unui eveniment sau frecvența este raportul dintre numărul de experimente în care a existat acest termen Soby, la numărul tuturor experimentelor. Notăm frecvența evenimentului A prin W (A), apoi, prin definiție, exerciții
6. Frecvența evenimentului. Determinarea statistică a probabilității
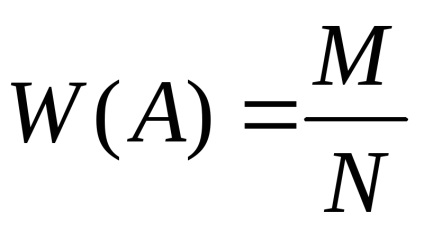
unde M - numărul de experimente în care evenimentul a avut loc și N - numărul tuturor experimentelor.
Frecvența evenimentelor are următoarele proprietăți:
Frecvența evenimentelor aleatoare de acolo număr între zero și unu: 0 Frecventa anumit eveniment U este unitate: W (U) = 1. Frecventa eveniment imposibil este zero V: W (V) = 0 Frecvența suma a două evenimente disjuncte A și B este egală cu suma frecvențelor acestor evenimente: W (A + B) = W (A) + W (B) Probabilitatea P (A) a evenimentului A cu definiție statistică numită frecvență W sale (A) într-o serie de evenimente care constau din numarul durerii Shogo de teste. Exemplu. Dintre cele 600 luate în mod aleatoriu 12 părți dau dovadă de respingere mi. Găsiți frecvența pieselor defecte. Decizie. Deoarece în acest exemplu, M = 12 și N = 600, atunci, prin definiție, au o divizare în frecvență 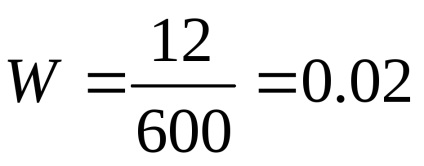
Notă. Pe lângă definițiile de mai sus și probabilitatea statistică clasică există și așa-numita definiție geometrică a probabilității. Faptul că atât definițiile clasice-mecanice și statistice sugerează că numărul de rezultate de curs elemente-Tary. Pentru a depăși acest neajuns, TSB-ditsya definiție geometrică a probabilității, care este aceea a riscului zonei adoptate a unei regiuni anumite COSV-oase, și pentru rezultatul elementar - punct de acest domeniu, cu condiția ca toate zonele elementare evenimente din regiune este egal cu 1.