curba de distribuție normală se numește curba normală sau Gauss. Această distribuție urmează legea, deschis trei savanți la momente diferite: Moivre în 1733 în Franța, de Gauss în 1809 în Germania și Laplace în 1812 în Franța.
în care u - înălțimea curbei direct deasupra orice valoare x predeterminată pe graficul de distribuție a frecvenței;
e - fundamentul sistemului logaritmilor naturali = 2718.
ais - numere care definesc poziția curbei în raport cu axa reală și să reglementeze domeniul său de aplicare.
Programează o distribuție normală este așa-numita curbă clopot simetric. Prin variația valorilor a și s, ne putem muta curba normală specifică a axei reale în sus și în jos și modifica dimensiunile.
Cantitatea A corespunde distribuției medie frecvență a unui eșantion mare (așteptare); s - abaterea standard a acestei distribuții. Astfel, parametrul a (așteptare) caracterizează poziția și parametrul s 2 (dispersie) - sub forma unei curbe normale.
lege normală variabilă aleatoare cu parametrii a = 0, s = 1 2. și anume N (0, 1), se numește un standard sau normalizat. iar curba normală corespunzătoare - standardul sau normalizat. Zona delimitată de această curbă este = 1.
Pentru orice combinație a curbei normale cu unitatea de transformare a efectua destul de simplă a distribuției inițiale prin scăderea valorii medii de la fiecare din punctele individuale Xi și împărțirea s.
Distribuția normală se caracterizează prin valori extreme caracteristică în ea sunt rare, iar valorile sunt apropiate de media - destul de des. Distribuția normală se numește, deoarece este foarte frecvente în naturale - cercetarea științifică și părea că „normal“ orice aparență accidentală în masă a unui atribut.
Curba normală va fi întotdeauna simetrice în raport cu un. Zona dintre curba și axa x este egal cu 1.
Proprietățile de distribuție teoretică normală
1) modul, mediana și media aritmetică egală sau au valori similare în mărime;
2) parametrii skewness și kurtosis sunt zero, As = 0 și Es = 0.
3) Efectuarea de obicei trei Sigma.
Comună pentru toate aceste curbe, în ambele distribuție normală aproximativ:
1. 68% din aria de sub curba se află în una s ale mediei în oricare direcție (adică o ± 1s);
2. 95% din aria de sub curbă se află două dintre s medii în oricare direcție (adică o ± 2s);
3. 99,7% din aria de sub curba se situează în domeniul de media a trei s în oricare direcție (adică o ± 3s).
Trei Sigma regula în limbajul teoriei probabilității:
Probabilitatea ca numărul de X se încadrează în intervalul de | X-mê
A) În cazul în care o caracteristică de distribuție simetrică pe fiecare parte a unei distanțe selective decaleze medie egală cu s, aceasta ar include 2/3 observații (distribuția normală, 68% din cazuri).
B) în intervalul X = [HSR ± 2s] este de 95% din cazuri.
B) în intervalul X = [HSR ± 3s] este de 99% din cazuri (în distribuția normală de 99,73% din cazuri).
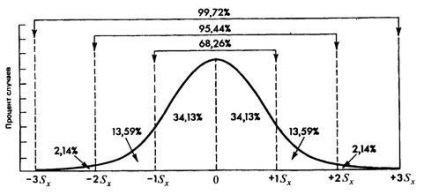
Fig. 3. Programează o caracteristică standard de distribuție normală.
Atunci când o probă omogenă obținută de la subiect la un mod predeterminat de distribuție normală, media aritmetică a acestor rezultate HSR și rezultatelor deviația standard s pentru un eșantion este norma statistică delimitare determinată [HSR ± s].
Fig. 4. Graficul de distribuție normală a caracteristicii
Normalitatea distribuției variabilei rezultante poate fi verificată prin calcularea indicilor aplatizare și asimetrie și compararea acestora cu valorile critice (criteriu NA Plohinskogo sau Pustylnik EI). Verificarea conformității cu distribuția empirică a valorilor normale, poate fi realizată în conformitate cu criteriul # 967; 2 -Pirsona.
Criteriul NA Plohinskogo
Marja de eroare calculată de asimetrici și aplatizării:
unde n este volumul eșantionului
Dacă Asimetria și aplatizare parametri depășesc de trei ori sau mai mult în valoare absolută reprezentativitatea lui greșeală, distribuția empirică este diferită de cea normală.
Criteriul EI Pustylnik
Se calculează valorile critice ale skewness și aplatizării
unde n este volumul eșantionului
În cazul în care valorile empirice ale skewness și kurtosis mai mult de valorile lor critice ca> acr și Es> ECR. distribuția empirică este diferită de cea normală.