definiție
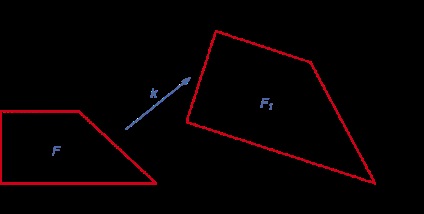
Transformarea similaritate - transformarea unei figuri F în figura F1. în care distanțele dintre punctele sunt schimbate în același număr de ori (k> 0).
regulă
Numărul k se numește coeficientul de similitudine, iar cifra F și F1 - place de: F
Dacă punctul de transformare X. X1 similaritatea. Y. Y1. X1 Y1 = k • XY.
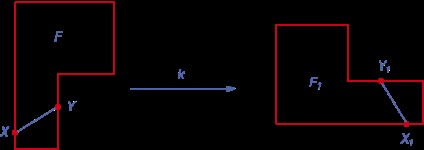
Proprietăți similitudine de transformare
o proprietate de 1
Transformarea similaritate se traduce printr-o linie dreaptă, taie - într-un segment, o rază - o rază.
proprietate 2
Transformarea similaritate păstrează unghiurile.
proprietate de 3
Transformarea similaritate transformă triunghiul într-un triunghi. Corespondenti părți ale acestor triunghiuri sunt proporționale și unghiurile corespunzătoare sunt egale.
proprietate de 4
Transformarea similaritate transformă un cerc într-un cerc.
proprietate de 5
În cazul în care transformarea similaritate cu coeficient k F ia forma în figura F1. zona lor sunt legate de:
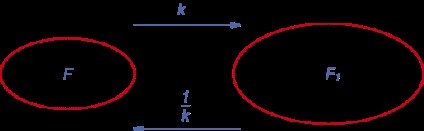
proprietate 6
Transformarea Inverse transformarea similaritate cu un coeficient k, există similitudine coeficient de transformare cu 1L.
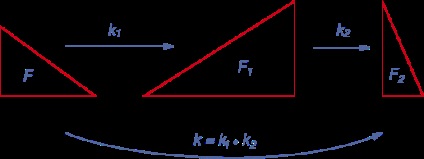
proprietate 7
Transformarea similaritate Compoziția cu coeficienți k1 și k2 este o transformare similaritate cu un coeficient k = k1 • k2.