Curs 8. lucru virtual și ecuația generală a dinamicii.
Acest curs acoperă următoarele subiecte:
1. deplasament posibile. Clasificarea obligațiunilor.
2. lucru virtuală cu echilibrul financiar al sistemului. Ecuația generală a staticii.
3. lucru virtuală cu mișcarea unui sistem material. Ecuația generală a dinamicii
4. Coordonatele generalizate.
5. Forțele generalizate.
6. Lagrange echilibru ecuații.
7. forța de inerție generalizată.
8. Ecuațiile Lagrange.
Studiul acestor probleme este necesară pentru studiul amortizorului în disciplina „piese Machine“, pentru a rezolva problemele din disciplinele „Teoria mașinilor și mecanisme“ și „Rezistenta materialelor“.
Posibil mișcare. Clasificarea obligațiunilor.
Atunci când studia corpurile de echilibru prin așa-numitul echilibru static geometrică necesar să se ia în considerare fiecare dintre corpurile în mod individual, prin înlocuirea comunicarea respectivă suprapusă reacții necunoscute în prealabil. În cazul în care numărul de corpuri într-un sistem mare, în acest fel devine foarte greoaie și este asociată cu necesitatea de a rezolva un număr mare de ecuații cu multe necunoscute.
O trăsătură distinctivă a metodei care rezultă din activitatea virtuală este faptul că, în cererea sa nu sunt luate în considerare efectul link-uri prin introducerea unor reacții în prealabil necunoscute, precum și prin luarea în considerare mișcările pe care le pot spune punctul de sistem, în cazul în care pentru a deduce sistemul din poziția pe care o ocupă. Aceste mișcări sunt numite în vozmozhnymiperemescheniyami mecanica.
Luați în considerare posibila deplasarea punctului M pe tija fixată pe suprafața fixă a balamalei D (Figura 2a). Desigur, bara vă permite să mutați un punct de pe suprafața sferică în orice direcție și la orice distanță. Toate aceste mișcări sunt posibile. Poate că, de altfel, în mișcare și în jos. Dar această mișcare nu ar trebui să fie numit posibil, deoarece link-ul tijei rupt.
În plus, capacitatea de a muta va numi doar cilindree mică, ca o mică parte a traiectoriei, că aceasta poate fi înlocuită cu o tangentă segment de linie dreaptă.
Putem formula acum definiția posibilă mișcare.
Capacitatea de a muta punctul sistemului de material va fi numit mișcarea infinitezimal permisă de constrângerile sistemului.
Capacitatea de a muta un sistem de puncte trebuie să îndeplinească două condiții:
1) trebuie să fie infinit de mic, deoarece sistemul va trece la o altă poziție în care condițiile de echilibru pot fi diferite sub deplasări finite;
2) trebuie să fie de așa natură încât, cu toate constrângerile impuse asupra sistemului sunt menținute, pentru că altfel vom schimba punctul de vedere al sistemului mecanic considerat (sistemastanet altele).
De exemplu, în mecanismul manivelă arătat în mișcare Fig.1 punctele OA poziția manivelei OA1 să nu fie considerat posibil, deoarece în această poziție a mecanismului în condiții de echilibru și forțe vor fi diferite. În mod similar, nu ar trebui să fie considerată posibilă deplasarea chiar minusculă a unui punct din tija de-a lungul liniei BD; ar fi posibil dacă la punctul B în locul cursorului ar pivota de cuplare, și anume atunci când mecanismul ar fi diferit.
Astfel, posibila deplasarea sistemului de noi numim orice set de puncte de deplasare infinitezimale ale sistemului permise la momentul toate constrângerile impuse asupra sistemului. mișcare posibilă a oricărui punct al sistemului va fi reprezentat de vectorul elementar. îndreptate spre deplasare.
În general, pentru puncte și sisteme de telefonie pot exista diferite deplasari in mai multe posibile (deplasări și noi nu considerăm diferit). Cu toate acestea, pentru fiecare sistem, în funcție de natura legăturilor impuse pe ea, puteți specifica un anumit număr de mișcări independente reciproc că orice altă mișcare posibilă va fi obținut ca sumă geometrică. De exemplu, o minge întinsă pe niște plane (sau de suprafață), poate fi deplasată de-a lungul planului unei multitudini de direcții. Cu toate acestea, orice mișcare posibilă poate fi obținut ca suma a două mișcări de-a lungul și situată în planul perpendicular axe ().
Numărul de independente între ele, deplasările posibile ale sistemului numit numărul de grade de libertate ale sistemy.Tak discutat mai sus șirag de mărgele pe un plan (sau de suprafață) în cazul în care acesta este considerat ca un punct material are două grade de libertate. La mecanismul cu manivelă este, evident, un grad de libertate.
La punctul de material liber - 3 grade de libertate (independent 3 se va deplasa de-a lungul axe perpendiculare între ele). corp rigid gratuit are șase grade de libertate (mișcări independente sunt 3 mișcări de translație de-a lungul celor trei axe de rotație și în jurul acestor axe).
La aceasta trebuie să adăugăm câteva observații.
În primul rând. Chiar numele acestor mișcări arată că acestea sunt posibile numai, dar nu este obligatoriu; că aceste mișcări dintr-o anumită poziție a sistemului poate fi de multe; că printre ei există doar un singur valabil (În cazul în care comunicarea - nu este fixă, se modifică odată cu trecerea timpului, mișcarea reală nu poate fi una dintre posibilele); că aceste mișcări nu apar sub influența forțelor aplicate sistemului, și, ca să spunem așa, la cererea noastră.
În al doilea rând. Datorită micimea astfel de mișcări sunt îndreptate de-a lungul tangenta la traiectoria si sunt astfel, direcția care coincide cu vectorul viteză. Această viteză, în acest caz, este, de asemenea, numit de viteză posibilă. nu este valid.
În al treilea rând. Dacă există legături între sistemul de puncte de material, posibila deplasarea acestor puncte sunt interconectate determinare dependență ecuații de constrângere.
Figura 2 prezintă câteva exemple de posibile deplasări ale punctelor unor sisteme materiale.
Din aceste exemple rezultă că singura mișcare posibilă a unui corp de rotație în jurul unei axe, un unghi de rotație mică. Iar deplasările posibile ale punctelor pot fi determinate cu ajutorul acestui unghi. Astfel, de exemplu, (Figura 2a și 2b).
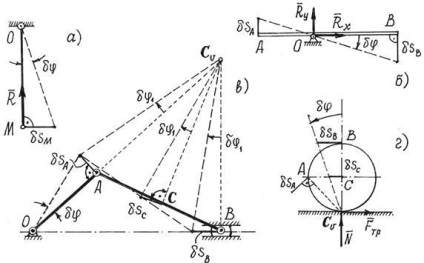
Deoarece direcțiile de mișcări sunt posibile direcția vitezei, deplasarea punctelor de legătură AB (ris.64, c) se determină cu ajutorul centrului instantaneu al acestei viteze de. O posibilă mișcare a întregului corp cu mișcare plan paralel - o rotație printr-un unghi mic față de o axă care trece prin centrul vitezei instantanee. Acest unghi poate fi determinat.
Din moment. atunci. și cursorul se deplasează punctul W. și S .. Aceasta este, deplasările tuturor punctelor mecanismului poate fi determinată printr-o singură mișcare posibilă, mișcarea de îngrijire a OA. prin unghi.
În mod similar, rotația cu un unghi mic în jurul centrului instantaneu de viteze. identifică posibila deplasare a punctelor de roți, care poate rula fără alunecarea de-a lungul unei linii drepte fixe (figura 2, g).
Activitatea forțelor aplicate sistemului financiar la posibila miscarea noi numim abilitatea de a lucra.
Dacă ne uităm la diferitele tipuri de sisteme materiale, s-ar putea găsi că activitatea elementară a reacțiilor de mai multe link-uri la deplasarea virtuală va fi egal cu zero. Astfel de legături, cantitatea de reacții posibile care funcționează pe orice mișcare posibilă este zero, numit constrângeri ideale. Astfel de lianți includ, de exemplu, toate conexiunile fără frecare.
Comunicații care nu se schimba cu timpul sunt numite staționare.
Există link-uri care sunt numite sau de retenție, sau o singură parte, în funcție de faptul dacă acestea împiedică mișcarea punctului în direcții opuse sau doar unul.
În unele sisteme materiale, există, de asemenea, relații destul de complexe, care limitează sau doar poziția sistemului, coordonatele punctelor sale sau mai mult și rata lor, derivată din coordonatele de timp. Prima se numește neolonome, geometrice, legături; în al doilea rând - holonomic, cinematică, non-integrabilă. Vom lua în considerare de acum înainte sisteme numai cu constrângeri neolonome.