Să presupunem că în spațiul tridimensional este fixat dreptunghiular sistem de coordonate Oxyz. având în vedere un punct, o linie dreaptă și doriți să găsiți distanța de la punctul A la linia A.
Vom arăta două metode care permit calcularea distanței de la un punct la o linie în spațiu. În primul caz, distanța de la punctele de constatare M1 la o linie dreaptă este redusă pentru a găsi distanța de la punctul M1 până la un punct H1. unde H1 - baza perpendicularei din tochkiM1 directe a. În al doilea caz, distanța de la un punct la un plan pentru a găsi merge ca înălțimea paralelogramului.
Prima metodă de a găsi distanța de la un punct la o linie în spațiu.
Deoarece prin definiție, distanța de la punctul de la linia M1 a - este lungimea perpendikulyaraM1H1. apoi, determinarea coordonatele punctului H1. putem calcula distanța necesară ca distanța dintre puncte și formula.
Astfel, problema se reduce la găsirea coordona o bază perpendiculară construită din punctul M1 la linia dreaptă a. Fă-l simplu: punctul H1 - este punctul de intersecție al liniei cu un plan care trece prin punctul M1 perpendicular pe linia A.
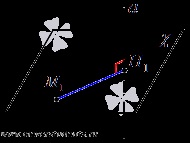
În consecință, algoritmul pentru a determina distanța de spațiu tochkido pryamoyav. este după cum urmează:
Formăm ecuația ca ecuația plan a planului care trece prin punctul dat perpendicular pe linia dat;
Determinăm coordonatele punctului H1 - punctul de intersecție al liniei și un plan (a se vedea articolul găsi coordonatele punctului de intersecție al liniei și care planul);
Se calculează distanța cerută de la punctul M1 la o linie dreaptă prin formula.
A doua metodă de a găsi distanța de la un punct la o linie dreaptă în spațiu.
Deoarece în problema ni se dă o linie de dreaptă. putem determina vectorul de direcție și coordonatele unui punct M3. situată pe linia chinta. Apoi, coordonatele punctelor, și putem calcula coordonatele vectorului: (dacă este necesar, consultați articolul, coordonatele coordonatele punctelor de început și de sfârșit).
Amână vectori și punctele M3 și construiesc pe ele paralelogram. Această paralelogram înălțime a cheltuielilor M1H1.
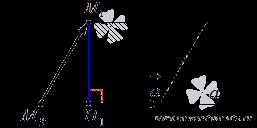
In mod evident, înălțimea paralelogramului este construită la distanță M1H1 dorit din tochkiM1 la linia a. S-au găsit.
Pe de o parte a zonei de paralelogram (notate cu S) poate fi găsit produsul cherezvektornoe vectorilor și formula. Pe de altă parte, aria unui paralelogram este egală cu produsul dintre lungimea laturilor sale la înălțime, adică, în care: - lungimea vectorului egală cu lungimea laturii considerate a paralelogramului. Prin urmare, distanța de la un punct predeterminat M1 la o anumită linie poate fi găsit din egalitatea de ambele.
Deci, pentru a găsi distanța de spațiu tochkido pryamoyav necesar
determină vectorul direcția liniei A (), și se calculează lungimea sa;
obține coordonatele unui punct M3. situată pe linia chinta. calculează coordonatele vectorului, găsiți produsul vectorial și cum să-l, și lungime;
calcula distanța cerută de la un punct la o linie în spațiu conform formulei.
Rezolvarea problemelor în găsirea distanța de la un anumit punct de la linia de date în spațiu.
Luați în considerare exemplul deciziei.
Găsiți distanța de la punctul de la linia.
Noi scriem ecuația planului care trece prin punctul perpendicular pe linia de date M1:
Găsim coordonatele punctului H1 - punctul de intersecție a planului și o linie dreaptă predeterminată. Pentru a face acest lucru, executați tranziția de la ecuațiile canonice ale unei linii drepte la ecuațiile de două planuri care se intersectează
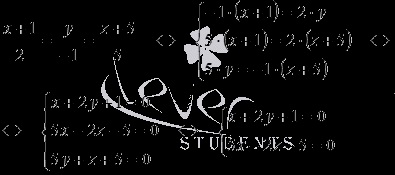
și apoi vom rezolva sistemul de ecuații liniare de către Cramer:

Rămâne să se calculeze distanța cerută de la punctul de la linia dreaptă ca distanța dintre punctele u :.
Numerele din numitorul fracțiunilor din ecuația canonică a liniei sunt coordonatele corespunzătoare ale vectorului liniei drepte, adică - vectorul direcția liniei. Se calculează lungimea :.
Este evident că linia trece printr-un punct, atunci vectorul cu punctul inițial și punctul final acolo. Găsim produsul transversală a vectorilor:

Acum avem toate datele pentru a folosi formula de calcul a distanței de la un anumit punct într-un anumit plan :.
.
Dispunerea reciprocă a liniilor în spațiu