
Distanța dintre liniile oblice este lungimea totală a perpendiculara lămuresc realizat.
Fig. 69 vom vedea un linii de oblic și b. paralel cu planul făcut pentru claritate și. în cazul în care sunt aceste linii. Distanța d dintre liniile a și b este lungimea MN lor perpendiculare comune.
Fig. 69. Distanța dintre liniile oblice
Rețineți că valoarea d este distanța de la orice punct de pe o linie dreaptă la planul (și în general din orice punct al planului cu planul). Prin urmare, în cazul în care problema specifică comună perpendicular pe două linii oblice nu este vizibil, puteți căuta distanta de la orice punct convenabil de prima linie la un plan care trece printr-o a doua linie paralelă cu prima linie dreaptă și va fi distanța dintre cele două linii.
12.1 Exemple de rezolvare a problemelor
Luați în considerare trei sarcini. Primele două sunt relativ simple, iar al treilea corespunde nivelului C2 problemei la examenul la matematică.
Problema 1. Găsiți distanța dintre marginile oblice ale unui tetraedru regulat a cărui lungime de margine este egal cu 1.
Decizie. Fie ABCD un tetraedru regulat cu margine 1. Considerăm distanța dintre liniile AD si BC. Fie M AD punctul de mijloc, N mijlocul BC (fig. 70).
Fig. 71. Problema 2
Prin urmare, distanța dintre linii drepte AB și BC 1 1 este distanța de la orice punct al liniei drepte BC 1 la D 1. 1 AB plan ia în mod convenabil, de exemplu, punctul B.
Distanța de la punctul B la planul AB 1 D 1 este distanța de la punctul A 1 până la un plan dat (deoarece segmentul A B 1 acest plan este împărțit în jumătate). O distanță de la A 1 la planul AB 1 D 1 A 1 este înălțimea H a piramidei triunghiulare AB 1 A 1 D 1.
p este baza piramidei AB 1 D 1 triunghi echilateral cu latura 2. Muchiile laterale 3 a piramidei egală cu 3. Prin urmare, piramida este regulat, iar punctul central al triunghiului H 1 D 1 AB.
AH lungime interval egală cu raza cercului circumscris triunghiului AB 1 D 1:
AH = 2 p 3 = p 6: 3
Apoi, în conformitate cu teorema lui Pitagora obținem:
A H = AA 1 1 2 3 AH = 2:
Aceasta este distanța necesară între liniile AB 1 și BC 1. p
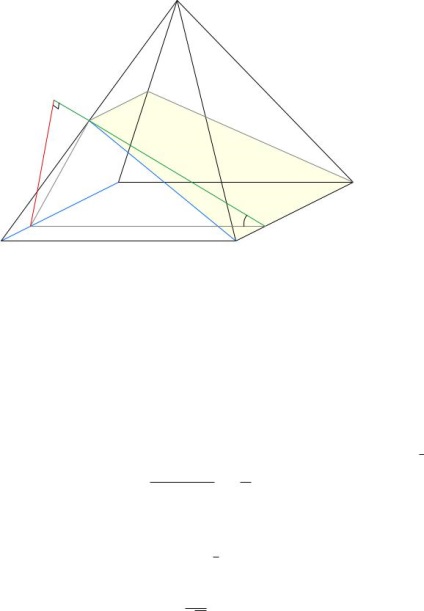
Problema 3. Piramida patrulateră regulată SABCD (cu vârf S) este egală cu lungimea fiecărei nervuri 4. Punctul de K SA la mijlocul coaste. Găsiți distanța dintre liniile AD și BK.
Decizie. Fig. 72 este o vedere în secțiune a planului piramidei KBC; Această secțiune este un BKLC trapez isoscel.