[Math] \ bar r_1 = (x_1, y_1, z_1) [/ math] - vectorul raza unui punct de pe linia;
[Math] \ bar s_1 = (l_1, M_1, N_1) [/ math] - vector pe direcția dreaptă;
[Math] d _ [/ math] - distanța de la un punct la o linie.
[Regula] Formula
Pentru un punct și o formulă de distanță linie dreaptă de forma:
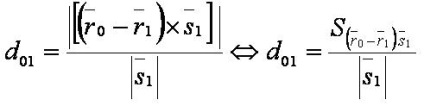
Distanța de la punctul de la linia este egal cu raportul dintre modulul produsului vectorial al vectorilor (r0 -R1) s1 și lungimea vectorului s1. Sensul geometric formula: lungime - este lungimea înălțimii paralelogram (formată din vectorii (r0 -R1) și s1), a redus la baza paralelogramului ca vector (s1), care este egal cu raportul dintre aria paralelogramului lungimea bazei.
Formula distanta de la un punct la o linie formă de coordonate în, este:
[Regula] EXEMPLUL
punct dat și linia: [matematica] (- 4; 3; 5) [/ math] și [matematica] \ frac = \ frac = \ frac [/ matematică].
Găsiți distanța dintre ele.
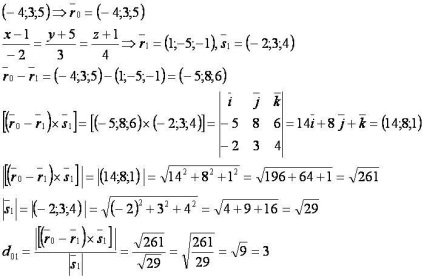
[Edit] Alte formule:
[Edit] Link-uri
- Korn H. Korn T. matematică Manual pentru Oamenii de știință și ingineri. M. Science, 1970.
- Membru: Logic-samara