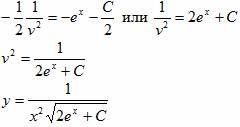Differential ecuația y „+ a0 (x) y = b (x) y n se numește ecuația Bernoulli.
Deoarece pentru n = 0 se obține printr-o ecuație liniară și când n = 1 - cu variabile separabile, atunci presupunem că n ≠ 0 și n ≠ 1. despartitor ambele părți ale (1) y n. Apoi ne-am stabilit, avem. Substituind această expresie, obținem, sau, echivalent, z „+ (1-n) a0 (x) z = (1-n) b (x). Aceasta este o ecuație liniară, pe care știm cum să rezolve.
Exemplul 1: Găsiți soluția generală a ecuației y „+ 2xy = 2xy 3. Această ecuație Bernoulli cu n = 3. Împărțind ambele părți de y 3, apoi am face o schimbare și astfel încât ecuația poate fi rescrisă ca -Z „+ 4xz = 4x. Rezolvarea acestei ecuații prin metoda variatiei constantelor arbitrare. Obținem în cazul în care sau ceea ce este același lucru.
Exemplul 2. y „+ y + y 2 = 0
y „+ y = -y 2
Divide prin 2 y
y „/ y 2 + 1 / y = -1
Facem schimbarea:
z = 1 / y n-1. și anume z = 1 / y 2-1 = 1 / y
z = 1 / y
z '= -y' / y 2
Obținem: -z '+ z = -1 și z' - z = 1
În plus, este necesar să se găsească și z expres y = 1 prin el / z.
Exemplul 3. xy „+ 2y + x 5 y 3 e x = 0
Decizie.
a) Decizia prin ecuația lui Bernoulli.
Reprezentat ca: xy „+ 2y = -x 3 5 y e x. Această ecuație Bernoulli cu n = 3. Impartind ambele părți ale ecuației 3 pentru a se obține y: xy „/ y 3 + 2 / y 2 5 = -x e x. Efectuarea de substituție: z = 1 / y 2. Apoi, z '= - 2 / y 3, și, prin urmare, ecuația poate fi rescrisă ca: -xz' / 2 + 2z = -x 5 e x. Această ecuație neomogenă. Să considerăm ecuația omogenă corespunzătoare: -xz „/ 2 + 2z = 0
1. Rezolvarea acestei ecuații, obținem: z „= 4z / x
Integrarea, obținem:
ln (z) = 4ln (z)
z = x 4. Privind acum soluția ecuației inițiale în forma: y (x) = C (x) x 4. y '(x) = C (x)' x 4 + C (x) (x 4) '
-x / 2 (4C (x) x 3 + C (x) „x 4) + 2y = -x e x 5
-C (x) 'x 5/2 = -x e x 5 sau C (x)' = 2e x. Integrarea, obținem: C (x) = x ∫2e dx = 2e x + C
Din starea lui y (x) = C (x) y, obținem: y (x) = C (x) y = x 4 (C + 2e x) sau y = Cx + 2x 4 4 e x. Deoarece z = 1 / y 2. obținem: 1 / y 2 = Cx + 2x 4 4 e x
b) o decizie prin schimbarea variabilelor
y = uv
x (u'v + uv „) + 2UV + x 5 u 3 v 3 e x = 0
v (x u '+ 2u) + XUV' + x 5 u 3 v 3 e x = 0
a) xu „+ 2u = 0
sau ln (u) = ln (x -2). În cazul în care u = x -2
b) XUV „+ x 5 u 3 v 3 e x = 0
x x -2 v „+ x 5 x -6 v 3 e x = 0
v „/ x + v 3 e x / x = 0
v „+ v 3 e x = 0