În acest articol, vom discuta despre metodele de rezolvare a ecuației lui Bernoulli. Pentru a consolida materialul în detaliu ia în considerare soluția de exemple.
ecuație diferențială Bernoulli are forma. Când n = 1, această ecuație devine o ecuație diferențială cu variabile separabile.
Una dintre metodele de rezolvare a ecuației diferențiale Bernoulli este acela de a reduce la o ecuație diferențială neomogen liniară a primului ordin al introducerii unei noi variabile. Într-adevăr, avem o ecuație diferențială și Bernoulli se va uita la o astfel de substituție
Deoarece ecuația diferențială se reduce la ecuația diferențială neomogenă Bernoulli liniară a primului ordin. După rezolvarea acestei ecuații și inversul substituției obținem soluția dorită.
Să considerăm următorul exemplu.
Găsiți soluția generală a ecuației lui Bernoulli.
În exemplul nostru. Vom introduce o nouă variabilă, atunci. După schimbarea transformărilor variabile și mici obținem prima comanda LNDU
Am rezolva prin metoda de variație de constante arbitrare.
Pentru a face acest lucru, mai întâi vom găsi soluția generală a ecuației diferențiale.

z = 0 este, de asemenea, o soluție a unei ecuații diferențiale, deoarece acesta devine o funcție de identitate la zero z. Acest caz poate fi descrisă de ecuația când C = 0. Astfel, soluția generală a ecuației diferențiale este unde C - constantă arbitrară.
Acum vom varia constant arbitrar, adică să accepte soluția generală a ecuației diferențiale. prin urmare
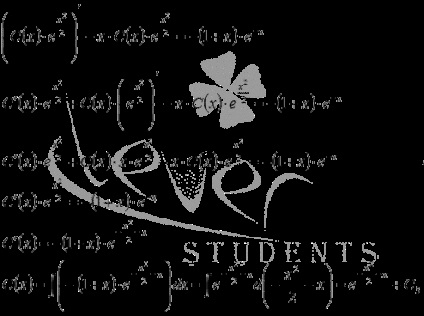
unde C3 - o constantă arbitrară.
Astfel.
A lăsat să-și petreacă schimbarea inversă. Din moment ce am presupus că. Aceasta este o soluție generală a ecuației lui Bernoulli originală.
Luați în considerare o altă metodă de rezolvare a ecuației diferențiale Bernoulli bazată pe reprezentarea funcției necunoscute y ca produs al funcțiilor u (x) și v (x).
În acest caz. După înlocuirea în ecuația lui Bernoulli obținem
Dacă funcția v nenul ia o soluție particulară a ecuației diferențiale, vom ajunge la egalitatea
în cazul în care și defini funcția u.
Rezolvăm exemplu în acest fel, a devenit clar tuturor.
Rezolva problema Cauchy, y (0) = 1.
Cu alte cuvinte, dorim să găsim o soluție particulară a ecuației diferențiale cu condiția y inițială (0) = 1.
După împărțirea pe ambele părți cu 2 x + 1 este clar că avem ecuație diferențială Bernoulli.
În primul rând, vom găsi soluția generală.
Să presupunem y = u ⋅ v. atunci ecuația devine
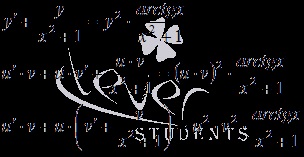
Am găsit o soluție particulară a ecuației diferențiale cu variabile separabile, diferit de zero.
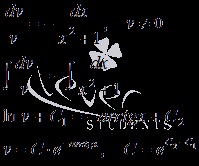
Ia soluții private.
Înainte de a lua fiecare dintre integralele separat, observăm că u = 0 este o soluție.
Integrala de pe partea stângă, este ușor de găsit din tabelul primitivelor:
Pentru a găsi integrantă arctgx = z accepte și să utilizeze metoda de integrare de către părți:

De unde - toate deciziile ecuației lui Bernoulli.
Rămâne să găsească o anumită soluție ce satisface condiția inițială y (0) = 1. Deoarece, atunci. În consecință ,.
Astfel, - soluția dorită a problemei Cauchy.
- Èl'sgol'ts LE ecuații diferențiale și calculul variațiilor.