Prin deformare îndoire se înțelege că impactul forțelor externe asupra corpului, ceea ce duce la o schimbare de curbură a corpului.
Fig. 1 prezintă un caz special de îndoire - indoire transversală a barei sprijinindu-se pe suport. Span AB = l. Curbare forța F este aplicată bara la punctul O (AO = OB). OO1 = Dh - deflecție în drept punct O. Hooke aplicat la deformare transversale îndoire pot fi scrise
unde b - coeficientul de îndoire în funcție de alte proprietăți de material, dimensiunea și forma barei.
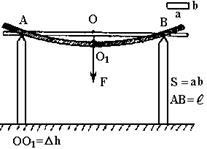
Când deformarea îndoire a liniei drepte bară transversală inițial bara axa ZZ (Fig. 2), sub forța F este curbată, iar secțiunea transversală S, paralel una cu alta flexiune, S // S, sunt rotite una față de cealaltă. Fibrele B1 bar superior A1 sunt scurtate și B2 A2 de jos - lungit. Cea mai mare compresie se produce în fibrele cele mai de sus și cea mai mare tensiune - în cea mai mică. Fibrele sunt dispuse pe axa Z1 Z1 îndoit, dar lungimea sa nu se schimba. Acest strat este numit stratul neutru. Astfel, ruptura transversală a fibrelor are loc pe de o parte a axei Z se întinde, pe de altă parte - comprimarea în direcția longitudinală (de-a lungul axei Z) se extinde între fibrele schimbare. (Atomii de interacțiune electromagnetică dă naștere forțelor elastice).
În orice secțiune a momentului bară de îndoire acționează M și transversal (forfecare) forță FS. După cum se poate observa din Fig. 2, momentul încovoietor pentru secțiunea transversală distanțată de sprijin A la Z distanță, este egal cu: M = FA Z (această formulă este valabilă la 0 £ Z l / 2 £), Nr FA = FB = F / 2, deoarece cu condiția JSC = OB, astfel încât în cele din urmă momentul de încovoiere este:
Din formula 3, momentul de încovoiere variază de la o secțiune la alta și atinge valoarea sa maximă la punctul O:
FS forță de forfecare pe întreaga lungime a barei va fi constantă și egală cu:
bara de deviere atinge valoarea sa maximă la Dh O secțiune unde maximul momentului de încovoiere acționează Mmah.
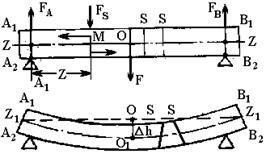
Calculele arată că magnitudinea mai mare deviere a este dată de:
unde E - modulul de elasticitate, modulul lui Young; J - momentul de inerție al secțiunii transversale a scînduri, în raport cu axa centrală.
În cazul unei secțiuni dreptunghiulare a plăcii cu laturile a și b. în care a> b, momentul secțiunii transversale de inerție este egală cu:
Substituind ecuația (4) și (7) în (6) obținem:
în cazul în care modulul de elasticitate la întindere E este determinată de deformarea îndoire transversală ar fi: