momentul static în raport cu punctul axa este produsul punctului de masă la o distanță de o linie dreaptă.
Să considerăm o curbă plan, a cărui densitate este egală. în timp ce greutatea curba egală cu lungimea sa, descoperim curba cuplului static în raport cu axa.
Lăsați curba dată de ecuația. Luați în considerare un punct de pe curba și curba de tăiat lungimea elementară porțiune. care conține punctul. Dacă presupunem că porțiunea de greutate egală. concentrată în punctul. punctul elementar, curba cuplului static adică scăzută în raport cu elementul axa este. Apoi, momentul static al întregului în raport cu axa curbei. Este formula.
Formula de calcul al curbei cuplului static în raport cu axa similar redată. .
Definiția. Centrul de greutate al curbei - acesta este un punct că, dacă nu se concentrează întreaga masă a curbei, momentul său static în raport cu o axă care nu intersectează curba, va fi egală cu momentul static al întregii curbei.
Prin urmare, vom obține formule pentru a găsi centrul de greutate al curbei de coordonate omogene.
În cazul în care curba este dată de ecuația în mod explicit. coordonatele curbe ale centrului de greutate sunt date de
Exemplul 1: Găsiți momentul static al unui semicerc cu privire la diametrul său.
Aranjați un semicerc, astfel încât diametrul său este pe axa. și centrul la origine.
Ecuația semicerc superioară. Noi găsim semnificația radicand în formula pentru a calcula momentul statistic. Substituind în formula, vom obține un răspuns.
Exemplul 2: Găsiți momentul static în raport cu axa arcului și coordonatele centrului de greutate al astroidă situat în primul trimestru.
Noi scriem ecuațiile parametrice astroidă
Formula de calcul a momentului static când curba este dată de ecuațiile parametrice.
Noi calcula radicand
Substituind formulă, constatăm că valoarea momentului static
Găsim coordonatele centrului de gravitate curbei.
Din cauza simetriei. Găsim ordonata centrului de greutate cu formula
momente statice și coordonatele centrului de greutate al cifrelor plane
Considerăm cazul în care forma este uniformă, adică, densitatea acestuia la fiecare punct este egal cu 1. Să cifra este un trapez curbilinie, delimitat graficul de mai sus a funcției. Distingem benzi verticale infinit înguste elementar. Prin adoptarea acestei benzi de aproximativ dreptunghi, găsi masa egală cu suprafața. Pentru a determina punctele elementare corespunzătoare benzii presupunem masa intreaga este concentrată în centrul de greutate, adică centrul dreptunghiului. Punctul de material care rezultă la distanță de axa de o distanță. la o distanță de axa. care este aproximativ egal. Apoi, sunt momente elementare și. De aici obținem formula
Coordonatele centrului de greutate al unui trapez curbiliniu uniform definită prin formulele.
În cazul unei definiții explicite a ecuației funcției. avem
Exemplul 3. Găsiți momentul static în raport cu axa și centrul de greutate al coordonatelor figura delimitate axa și un arc de cicloidă.
Scriem ecuațiile parametrice ale cicloidei
Înlocuind aceste ecuații în formula de calcul a momentului static în raport cu axa figurilor:
Găsim coordonatele centrului de greutate al figurii. Din moment. o cifră simetrică în raport cu o linie dreaptă. Prin urmare, abscisa centrului de greutate. Ordonata centrului de greutate găsit de formula.
Se calculează aria figurii
Având în vedere că momentul statică corespunzătoare este luată în calcul, găsiți ordonata a centrului de greutate. Astfel, centrul de greutate al figurii este punctul.
Pentru prima dată, aceste teoreme a găsit un matematician Pappus alexandrin în secolul 3 î.Hr.
În Evul Mediu multe dintre realizările științei antice a fost pierdut în Europa. În teorema din secolul al 17-lea redeschis matematician elvețian Guldin.
Prima teorema lui Pappus-Guldin. Suprafața formată prin rotirea unei curbe în jurul axei nu se intersectează, este egală cu produsul dintre lungimea curbei pe traseul parcurs de centrul de greutate al curbei.
În cazul rotației în jurul axei teoremă exprimată prin formula
Dovada. Luați în considerare cazul unei curbe plan, atunci când este dat în mod explicit de ecuația. Ordonata curbei este centrul de greutate al formulei. Substituind formulă pentru găsirea și multiplicarea cuplul de sarcină este egală cu lungimea curbei. obține
Apoi multiplica ambele părți prin:
Pe partea dreaptă a acestei egalități este suprafața corporală, formată prin rotirea în jurul axei curbei.
În partea stângă este produsul din lungimea curbei pe lungimea cercului. care descrie centrul de greutate. Acest lucru dovedește teorema.
Exemplul 1. Găsiți coordonatele centrului de greutate al unui semicerc de rază, cu centrul la origine coordonate situate în jumătatea superioară.
Prin simetrie, abscisa a centrului de greutate. Găsim ordonata centrului de greutate, folosind prima teorema lui Pappus-Guldin. Suprafața formată prin rotație în jurul axei curbei. Este o sferă, zona sa. Lungimea curbei este egală cu jumătate din circumferință. Înlocuind aceste valori în Eq. găsi ordonata a centrului de greutate.
Exemplul 2. Găsiți suprafața semicercului de rotație în jurul tangent paralel cu diametrul său.
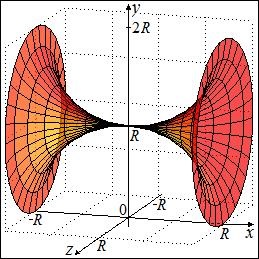
Apoi, raza cercului descris de centrul de greutate în timpul rotației în jurul tangenta semicercul egal. Din prima teorema Papp-Guldin au formula. Prin urmare, suprafața necesară
A doua teorema lui Pappus-Guldin. corp volum format prin rotirea unui plan figura în jurul axei sale nu se intersectează, este egală cu produsul de forma patrata pe traseul parcurs de centrul de greutate al figurii. În cazul rotației în jurul axei teoremă exprimată prin formula
Dovada. Luați în considerare cazul unei curbe plan, atunci când este dat în mod explicit de ecuația. Cifra sub graficul curbei este un trapez curbat. Ordonata centrului de greutate al figurii plane este formula. Aplicarea formulei de calcul a momentului static. Noi primim. Se înmulțește cu numărul de fiecare parte a acestei ecuații:
Pe partea dreaptă este volumul solidului obținut prin rotirea în jurul axei curbei. Partea din stânga este produsul bucăți pătrate pe lungimea cercului descris de centrul de greutate al figurii.
Exemplul 3. Găsiți coordonatele centrului de greutate al unui semicerc de rază R, cu centrul la origine, situată în jumătatea superioară.
Noi folosim a doua teorema lui Pappus-Guldin. Când se rotește în jurul axei formează o minge semicerc. Volumul mingea este egal. Zona semicercului. Înlocuind aceste valori în Eq. Ne găsim.