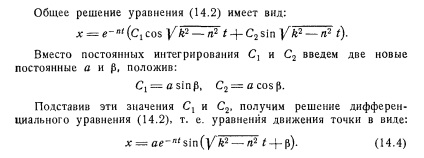Centrul de greutate al triunghiului
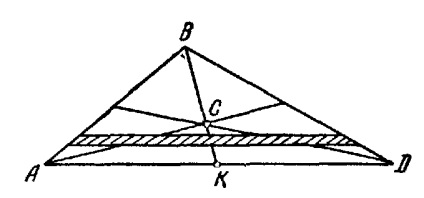
Centrul de greutate al zonei trapezoid
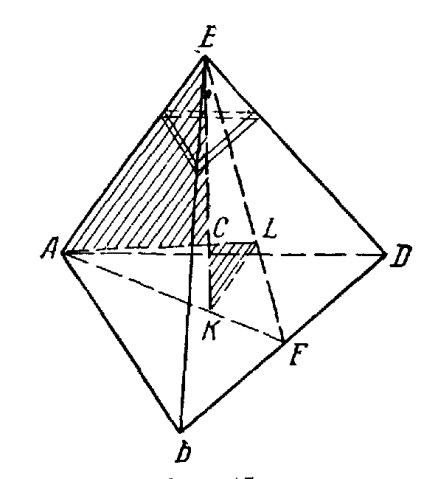
Centrul de greutate al suprafeței unui trapez trebuie să se întindă pe o linie dreaptă FK, care leagă punctele de centru laturile paralele ale trapez.

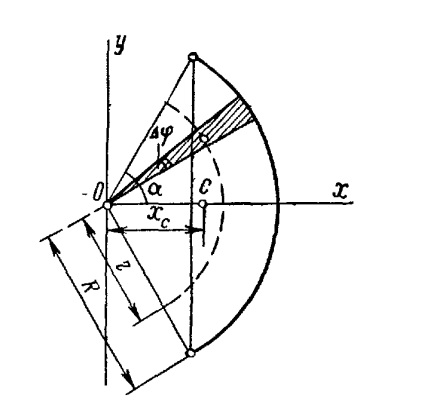
Centrul de greutate al unui arc de cerc
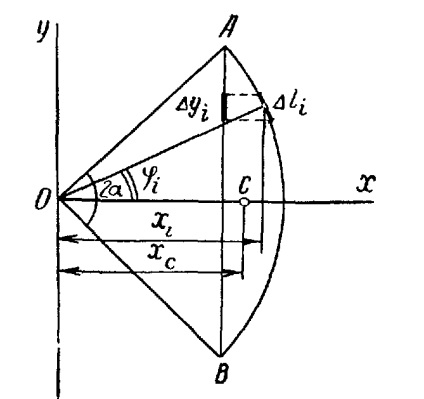

Centrul de greutate al gama de domenii sectoriale
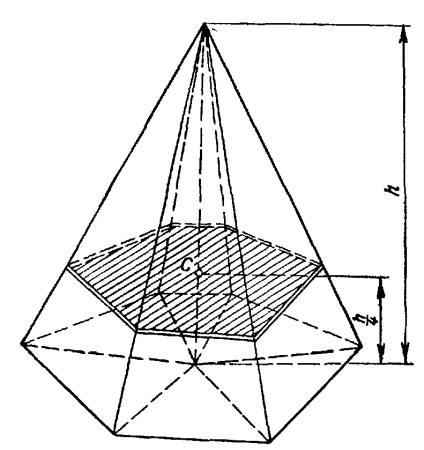
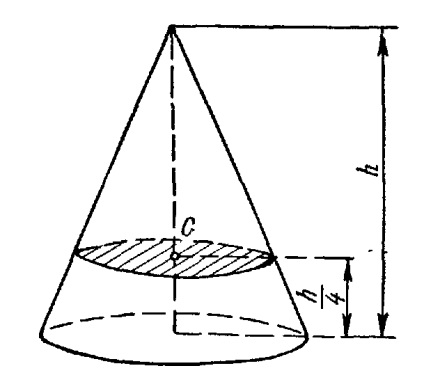
Centrul de greutate al volumului de piramida cu patru fete
Acest rezultat poate fi aplicat la piramida multe fețe. deoarece aceasta poate fi împărțită în piramidă patrulateră, spargerea unui poligon în triunghiuri baza sa.
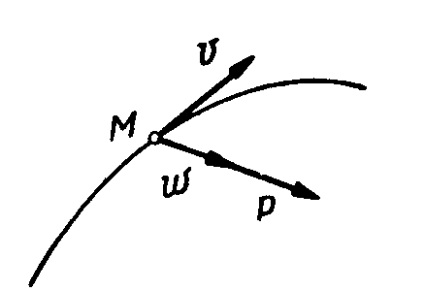

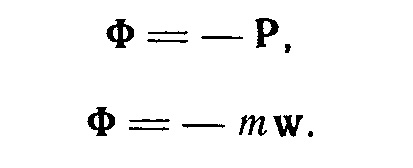
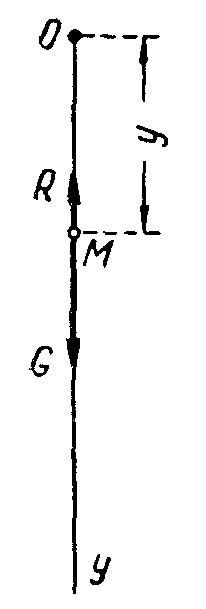
Forța de inerție a punctului material este o adevărată putere, care este un punct material de rezistență schimba viteza, și este aplicat pe corp, care conferă această accelerare punct.
La neuniforma mișcarea curbilinie a unei forțe punct de inerție F este descompus în două componente dirijate de-a lungul tangentei cale și comitent normal (fig. 4).
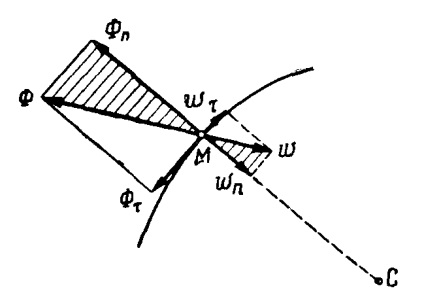
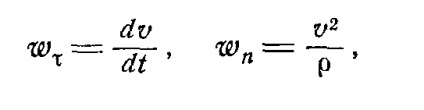
Modulele sunt forțe tangențiale și normale de inerție, numite în acest caz, inerția și centrifuge forțe de rotație
Obținut componente F # 964; și Fn se numește tangenta și forțele normale de inerție. Aceste forțe de inerție sunt îndreptate în sens opus accelerația tangențială și normală.
Dinamica unui punct material liber
Ecuații diferențiale de mișcare a unui punct material liber în coordonate carteziene.
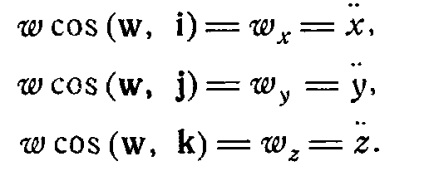
Ecuațiile naturale de mișcare a unui punct material
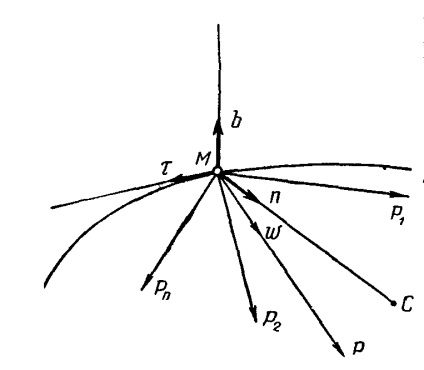

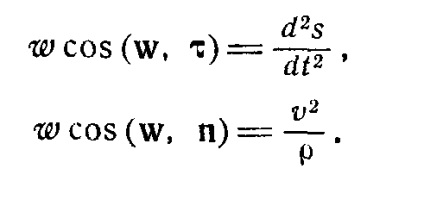
Din cinematicii cunoscut faptul că w vectorul accelerație se află în planul osculating și proiecția acestuia pe binormal la zero:
Cele două probleme principale ale dinamicii punctului
A doua problemă a dinamicii. Cunoscând forțele care acționează asupra materialului
Point, m masa sa, iar poziția inițială a punctului și viteza sa inițială, pentru a obține ecuațiile punctelor de mișcare.
Pentru a rezolva această problemă trebuie să fie în partea stângă a ecuațiilor de a substitui valoarea masei M și în partea dreaptă - suma proiecțiilor forțelor aplicate și ecuațiile rezultate integrate de două ori în timp.
există două constante, și, prin urmare, în integrarea a trei ecuații diferențiale de mișcare a unui punct va fi de șase picioare în integrarea ecuației diferențiale de mișcare pentru fiecare punct. Valorile acestor constante determinate de condițiile inițiale de conducere: trei valori de coordonate ale punctului și proiecția acestuia pe viteza cu trei axe, la un moment dat, de obicei (dar nu neapărat) la momentul inițial.
Luați în considerare următoarele cazuri schimba forța care acționează asupra punctului:
1) forță este constantă în mărime și direcție;
2) Forța depinde de timp;
3) Forța depinde de poziția unui punct în spațiu;
Rezistența depinde de viteza punctului.
Căderea liberă a rezistenței aerului corpului cu excepția.
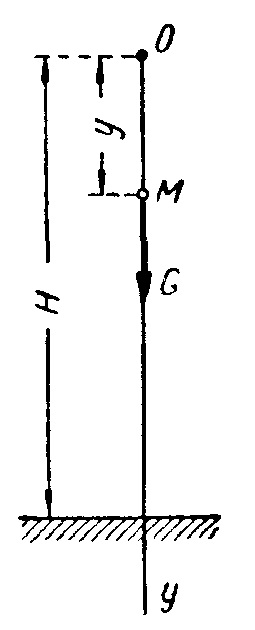
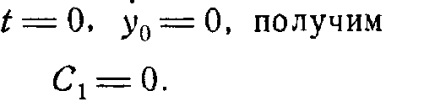
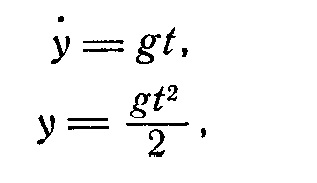
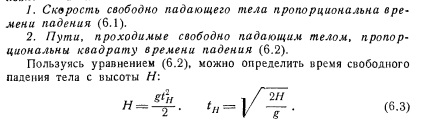
Mișcarea a corpului aruncat la un unghi față de orizontală, și exclude rezistența aerului.
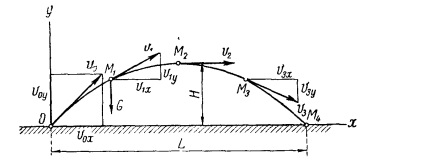
Naib. lift
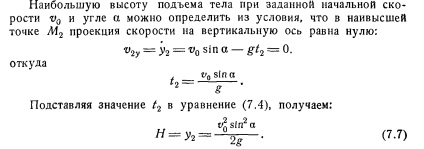
mișcarea de cădere a corpului cu rezistența aerului
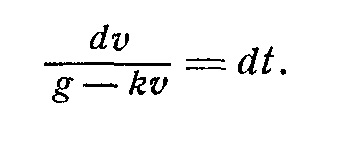
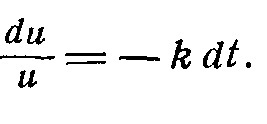
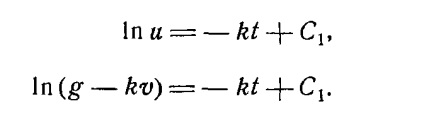
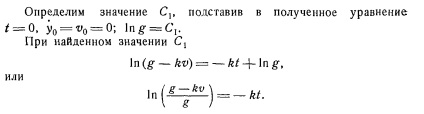


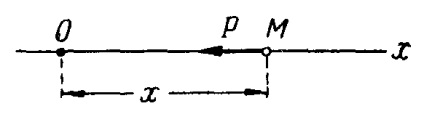
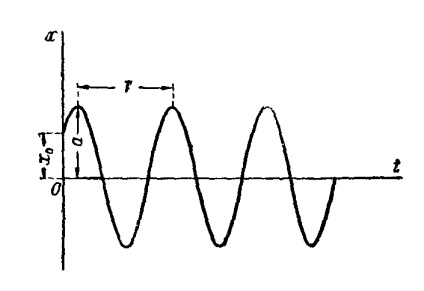
mișcare vibrațională MATERIAL PUNCT
Există patru cazuri principale de mișcare de vibrație a punctului-mat de masă:
oscilațiile gratuite care au loc sub acțiunea doar
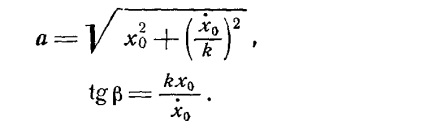

oscilațiile damped care au loc sub acțiunea unei forțe de restabilire și forță de rezistență la mișcare,
La punctul de rezistență la forța îndreptată întotdeauna în direcția opusă mișcării unui punct.
Ecuația este o ecuație diferențială de mișcare a unei particule sub acțiunea unei forțe de restabilire și o forță de rezistență proporțională cu viteza punctului.