§ 2.12. Coordonatele centrului de masă
În spațiul în care sistemul de coordonate dreptunghiular introdus, lăsați punctul de material este setat cu masa. momentul static al acestui punct în raport cu planul este produsul, și este notat
Momentul static de material relativ puncte plan de sistem finit definit de mase
În cele din urmă, în cazul în care greutatea este distribuită pe un anumit set, momentul static al corpului în raport cu planul definit de integrala,
unde - densitatea distribuției masei.
Centrul de greutate al corpului are coordonatele definite de ecuațiile
În special, în cazul în care există un trapez curbiliniu într-un plan delimitat deasupra și sub graficul axei funcției, uniform umplute cu densitate în masă, (Fig.57)
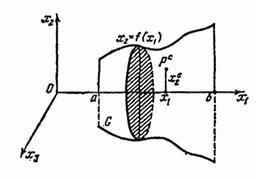
În partea dreaptă (1) este volumul corpului obținut din axa de rotație în jurul unui trapez curbat.
Astfel, avem binecunoscutul Gyuldina teorema: rotirea volumului corpul trapezoid curbilinii este egală cu suprafața sa multiplicat cu lungimea cercului descris de centrul de masă (gravitate) trapezului în jurul axei.
Dacă există o curbă uniformă,
unde - lungimea curbei în intervalul - elementul de lungimea arcului. de atunci
În partea dreaptă (2) este aria unei suprafețe de revoluție în jurul axei curbei. Astfel, ecuația (2) oferă o altă teoremă Gyuldina: aria suprafeței curbei de rotație egală cu lungimea arcului său, înmulțit cu lungimea cercului descris de centrul de masă al arcului în jurul axei.
Teoremele Gyuldina permite două valori cunoscute pentru a găsi a treia. De exemplu, în cazul în care coordonatele cunoscute ale centrului de greutate și cantitatea de rotație a corpului, este posibil să se determine aria unui trapez curbat, și așa mai departe. D.
Exemplul 1. Găsiți coordonatele centrului de greutate al trapezului curbat (Fig. 58).
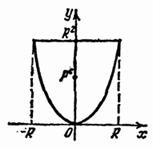
Să - centrul de greutate. Prin simetrie, este clar că (ne gândim). Găsiți aria unui trapez:
Volumul corpului obținut din rotirea în jurul axei este
Bazat mai întâi teorema Gyuldina
Exemplul 2. Găsiți volumul solidului obținut prin rotirea unui cerc cu centrul la raza punctului, în jurul axei (Fig. 59).
Este clar că centrul de greutate al cercului (omogen) să coincidă cu centrul geometric, adică. F .. suprafața unui cerc. Prin urmare, prima teorema Gyuldina
Exemplul 3. Găsiți zona de rotație suprafața corpului, discutată în Exemplul 2.
Această suprafață poate fi considerată ca o suprafață generată prin rotirea unui cerc în jurul unei axe. Lungimea circumferinței este egală. Prin urmare, a doua teorema Gyuldina
(Uniform centrul de greutate al circumferențială coincide cu centrul cercului).
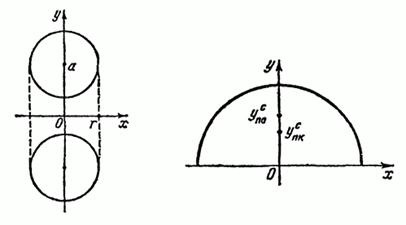
Exemplul 4. Găsiți centrul de greutate al unui omogen semicerc; semicerc.
Este cunoscut faptul că volumul unei sfere de rază egală cu, și egală cu suprafața mingea. Conform formulei (1) obținem (Fig. 60)
unde - ordonata centrului de greutate al semicercului.
Conform formulei (2), la centrul de greutate al ordonata avem semicercul
Momente. Th Pentru moment a unui punct de masă de material în raport cu planul este produsul
În cazul în care masele sunt distribuite pe un set măsurabilă cu densitatea,
Dacă punctul corespunzător este numit al doilea moment ordinea de inerție.
Mai mult decât atât, putem lua în considerare corpul -lea momente de ordine despre originea
în raport cu axa. De exemplu, momentul comenzii în raport cu axa poate fi scrisă