ecuație diferențială neomogenă liniară (LNDU) din ordinul doi cu coeficienți constanți are forma în care p și q - sunt numere reale arbitrare, iar funcția f (x) - continuă pe intervalul de integrare X.
Formulăm o teorema care arată forma în care să caute o soluție LNDU comună.
Soluția generală asupra ecuației diferențiale neomogene X liniar interval cu continuu pe intervalul de factor de integrare X și o funcție f continuă (x) este suma soluției generale a ecuațiilor diferențiale ordinare corespunzătoare liniare și orice soluție particulară a ecuației neomogenă inițială, adică.
Astfel, soluția generală a ecuației neomogene a doua diferentiale ordine liniar cu coeficienți constanți este suma soluției totale a doua ordinea corespunzătoare liniare ecuațiilor diferențiale ordinare cu coeficienți constanți și soluții particulare încep LNDU :. Este descris în articol omogen ecuații diferențiale a doua ordine liniare cu coeficienți constanți și rămâne să învețe să identifice.
Există mai multe metode pentru găsirea unei soluții special LNDU a doua ordine cu coeficienți constanți. Metodele sunt selectate în funcție de forma funcției f (x). pe partea dreaptă a ecuației. Noi le enumera și discuta soluții adecvate de ecuații diferențiale neomogene a doua ordine liniare cu coeficienți constanți.
Dacă f (x) este un polinom de gradul n-lea a f (x) = Pn (x). LNDU apoi soluția particulară este solicitată în forma în care Qn (x) - un polinom de gradul n. și r - numărul de rădăcini ale ecuației caracteristice egale cu zero. Deoarece - o soluție particulară a ecuației, factorii care determină polinomul Qn (x). Este metoda coeficienților nedeterminați ai ecuației.
Rezolva problema Cauchy.
Cu alte cuvinte, trebuie să găsim o soluție special de ordinul a doua ecuații diferențiale liniare neomogene cu coeficienți constanți, întrunind condițiile inițiale.
Știm că soluția generală a ecuației liniare neomogene este suma soluției generale a ecuației omogene corespunzătoare și o soluție particulară a ecuației neomogene, adică.
În primul rând, vom găsi o soluție generală LNDU alte credite la decizia privată.
S-au găsit. Pentru a face acest lucru, vom scrie ecuația caracteristică și pentru a găsi rădăcinile sale.
Rădăcinile sunt reale și diferite, așa.
Ne întoarcem la. Deoarece partea dreaptă a ecuației inițiale este un polinom de gradul al doilea și unul rădăcină al ecuației caracteristice este zero, atunci soluția particulară este solicitată în forma în care A, B și C - coeficienți nedeterminat. Acești factori determină ecuația.
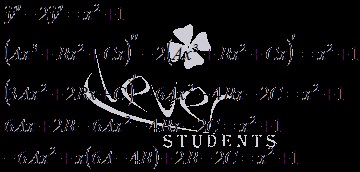
Echivalând coeficienții acelorași exponenți x. Ajungem la un sistem de ecuații liniare. Rezolvarea în vreun fel (dacă este necesar, consultați articolul, sistemele de ecuații algebrice liniare rezolvarea), obținem coeficienții nedeterminate necesari. În consecință ,.
Aceasta este o soluție generală a originalului liniare de ordinul al doilea ecuațiile diferențiale neomogene cu coeficienți constanți.
Rămâne de a găsi o anumită soluție care îndeplinește condițiile inițiale. Adică, este necesar să se definească astfel C1 și C2 în ecuația pentru a satisface condițiile.
Pe de altă parte.
Astfel, obținem un sistem de ecuații. Locație.
Prin urmare, soluția problemei Cauchy este funcția
Dacă funcția f (x) este reprezentat de produsul polinomului de gradul n și exponent, atunci soluția special LNDU a doua ordine căutată în forma în care Qn (x) - un polinom de gradul n-lea, r - numărul rădăcinilor ecuației caracteristice sunt egale. Coeficienții de Qn polinomului (x) se determină din ecuația.