regula lui Horner - o metodă pentru împărțirea polinomului
pe binom $ x-o $. Va lucra cu un tabel, primul rând conține coeficienții unui polinom predeterminat. Primul element din al doilea rând va fi numărul $ a $, luat din binomial $ x-a $:
După împărțirea gradului n-lea polinomiale la binomial $ x-un $, un polinom al cărui grad este unul mai puțin decât inițial, adică este egal cu $ $ n-1. aplicarea directă a sistemului de Horner este cel mai ușor de a arăta prin exemple.
Se împarte $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ la $ x $ 1, utilizând schema Horner.
Compilează un tabel cu două rânduri: un prim rând scrie coeficienți polinomiali $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $, aranjate în grade descrescătoare variabila $ x $. Rețineți că acest polinom nu conține $ x $ in primul grad, și anume, coeficient de $ x $ în primul grad este 0. Din moment ce împărțim de $ X- $ 1, a doua unitate de linie de scriere:
Vom începe să umple celulele goale în al doilea rând. În a doua celulă din al doilea rând a scrie numărul $ 5 $ prin simpla trecerea de la linia de celule prima corespunzătoare:
Completați celula următoare pe următorul principiu: $ 1 \ cdot 5 + 5 = $ 10:
In mod similar, umple, și un al patrulea celulă al doilea șir: $ 1 \ cdot 10 + $ 11 = Indicator 1:
Pentru a cincea celula obține $ 1 \ cdot 11 + 0 = 11 $:
Și, în sfârșit, pentru ultima, a sasea celula, avem $ 1 \ cdot 11 + (- 11) = $ 0:
Problema este rezolvată, rămâne doar să scrie răspunsul:
După cum se vede, numărul, dispus în a doua linie (între unu și zero), există coeficienți polinomiali obținute după împărțirea $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ pentru $ x 1 $. În mod natural, deoarece gradul de original polinom $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ egal cu patru, gradul de polinomului obținut $ 5x ^ 3 + 10x ^ 2 + 11x + 11 $ mai puțin pe unitate, adică . Acesta este egal cu trei. Ultimul număr din rândul al doilea (zero) înseamnă restul de divizare a polinomului $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ pentru $ x 1 $. În acest caz, restul este zero, adică polinoame împărțit în mod egal. Acest rezultat poate fi în continuare caracterizate după cum urmează: valoarea polinomului $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 la $ $ x = 1 $ este zero.
O și pot fi formulate sub forma: ca valoarea polinomului $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $ la $ x = 1 $ este zero, unitatea este o radacina a polinomului $ 5x ^ 4 + 5x ^ 3 + x ^ 2-11 $.
Împărțiți $ polinomul x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 $ la $ x + $ 3 pentru schema Horner.
Mai întâi, că $ expresie x + $ 3 trebuie să fie reprezentate în formă $ x - (- 3) $. schema din Horner va participa este de $ -3 $. Deoarece gradul de original polinom $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-patru este egal cu $ 47, rezultatul împărțirii unui polinom de gradul al treilea:
Acest rezultat înseamnă că
$$ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 = (x + 3) (x ^ 3 + 0 \ cdot x ^ 2 + 4x-17) + 4 = (x + 3) (x ^ 3 + 4x-17) + 4 $$
În această situație, restul de divizare $ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x- $ 47 la $ x + 3 este egal cu $ $ $ 4. Sau, ceea ce este același, valoarea $ polinom x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 la $ $ x = $ -3 $ egalează 4 $. Apropo, este ușor să verificați de două ori prin substituție directă $ x = $ -3 într-un anumit polinom:
$$ x ^ 4 + 3x ^ 3 + 4x ^ 2-5x-47 = (- 3) ^ 4 + 3 \ cdot (-3) ^ 3-5 \ cdot (-3) -47 = 4 $$.
Ie regula Horner poate fi utilizat dacă este necesar, pentru a găsi valoarea polinomului pentru o anumită valoare a variabilei. În cazul în care obiectivul nostru - pentru a găsi toate rădăcinile unui polinom, schema Horner poate fi aplicat de mai multe ori într-o succesiune - atâta timp cât nu a alerga afară de toate rădăcinile, așa cum sa discutat în exemplul №3.
Găsiți toate rădăcinile întregi ale polinomului $ x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45, utilizând schema Horner.
Coeficienții polinomului este considerat întregi, iar coeficientul de cel mai înalt grad al variabilei (adică, înainte de $ x ^ 6 $) este egal cu unitatea. În acest caz, rădăcinile întregi ale polinomului trebuie să fie căutat printre membrii liberi ai divizorii, și anume, printre divizori de 45. Pentru un anumit rădăcini polinomial astfel poate fi numărul de $ 45 de ani; \; 15; \; 9; \; 5; \; 3; \; 1 $ și $ -45; \; -15; \; -9; \; -5; \; -3; \; -1 $. Verificăm, de exemplu, numărul de $ 1 $:
După cum se vede, valoarea $ polinom x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45 dispus pe $ x = 1 este egal cu $ $ $ 192 alineatul (ultimul număr, în al doilea rând), mai degrabă decât $ cu 0 $, astfel încât unitatea nu este o rădăcină a acestui polinom. Deoarece cecul pentru unitatea nu a avut succes, vom verifica valoarea de $ x = -1 $. Tabel nou pentru acest lucru nu va fi, și va continua să se folosească de masă. №1, după ce au adăugat la acesta o nouă linie (a treia). Al doilea rând, care verifică valoarea $ 1 $, evidențiate în roșu, iar în discuția ulterioară nu-l vom folosi.
Puteți, desigur, doar rescrie tabelul din nou, dar de umplere manual va lua timp. Mai ales din cauza numere, dintre care de verificare va eșua, pot exista mai multe, și de fiecare dată pentru a înregistra un nou tabel este dificil. La calcularea „pe hârtie“ linia roșie poate fi pur și simplu, eliminându-se.
Astfel, valoarea $ polinom x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ la $ x de 45 = -1 $ este zero, adică numărul $ -1 $ este o rădăcină a acestui polinom. După împărțirea $ polinom x ^ 6 + 2x ^ 5-21x ^ 4-20x ^ 3 + 71x ^ 2 + 114X + $ 45 privind fasole $ x - (- 1) = x + 1 $ obține polinomul $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69X + $ de 45 ale căror coeficienți sunt luate din al treilea rând al tabelului. №2 (vezi. Exemplu №1). Rezultatul calculului poate fi, de asemenea, reprezentate sub forma:
Vom continua să caute rădăcinile întregi. Acum este necesar pentru a căuta rădăcinile polinomului $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69X + $ 45 de ani. Din nou, rădăcinile întregi ale polinomului sunt în căutarea printre divizorii mandatului său absolut - numărul de $ 45 $. Hai să încercăm încă o dată pentru a verifica numărul $ -1 $. Noul tabel nu va fi, și va continua să utilizeze tabelul anterior. №2, și anume Umple-l într-o altă linie:
Astfel, numărul de $ $ iar -1 o radacina a polinomului $ x ^ 5 + x ^ 4-22x ^ 3 + 2x ^ 2 + 69X + $ 45 de ani. Acest rezultat poate fi scris ca:
Luând în considerare ecuația (2), ecuația (1) poate fi rescrisă sub forma:
Acum este necesar să se caute rădăcinile polinomului $ x ^ 4-22x ^ 2 + 24x + $ 45, - desigur, printre divizorii mandatului său absolut ($ numărul $ 45). Verificați din nou numărul $ -1 $:

Numărul $ -1 $ este o rădăcină de $ x ^ 4-22x ^ 2 + 24x + $ 45 de ani. Acest rezultat poate fi scris ca:
ecuația Dată (4), ecuația (3) poate fi rescrisă sub forma:
Suntem acum în căutarea pentru rădăcinile polinomului $ x ^ 3-x ^ 2-21x + $ 45 de ani. Verificați din nou numărul $ -1 $:

Verificarea nu a reușit. Al șaselea rând distinge roșu și va încerca să verificați un număr diferit, de exemplu, numărul de $ 3 $:

În sold zero, prin urmare, numărul $ 3 $ - considerat rădăcina polinomului. Deci, $ x ^ 3 x ^ 2-21x + 45 = (x-3) (x ^ 2 + 2x-15) $. Acum ecuația (5) poate fi rescrisă ca:
Să ne verifica din nou numărul de $ 3 $:

Acest rezultat poate fi scris ca (o continuare a ecuației (6)):
Din ultimele paranteze arată că numărul $ -5 $, de asemenea, este o rădăcină a acestui polinom. Puteți, desigur, să continue punct de vedere tehnic schema Horner, verificarea valorii de $ x = -5 $, dar acest lucru nu este necesar. Astfel,
Numărul de $ 1; \; 3; \; $ 5 - rădăcinile polinomului. Mai mult, deoarece consola $ (x + 1) $ în al treilea grad, la $ -1 $ - rădăcina treilea ordin; deoarece $ bracket (x-3) $ în al doilea grad, cele $ 3 $ - rădăcina doilea ordin; deoarece $ bracket (x + 5) $ în primul grad, de $ x = -5 $ - rădăcina primului ordin (o singură rădăcină).
În general, proiectarea obișnuită a unui astfel de exemplu, constă dintr-un tabel, în care opțiunile sunt în mișcare rădăcini și răspunsuri:
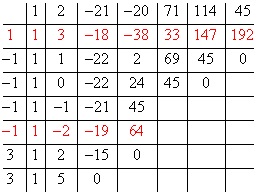
Din tabel se poate concluziona că am obținut anterior cu soluții detaliate:
Verificați dacă numărul de 2 $ și $ $ $ -5 sunt rădăcinile polinomului $ 3x ^ 6 + 9x ^ 5-28x ^ 4 + 6x ^ 3-30x ^ 2-30x + 100 $. Divizează polinomul dat la x-binomi $ 2 $ și $ x + 5 $.
Gradul de $ 3x polinomul ^ 6 ^ + 9x 5-28x ^ 4 + 6x ^ 3-30x ^ 2-30x + 100 este egal cu $ $ $ 6. După împărțirea în două grade predeterminate scădere polinom binomială predeterminată de $ 2 $, adică Acesta va fi egal cu $ 4 $.
Desigur, această metodă de selecție nu este foarte eficient în cazul general, atunci când rădăcinile nu sunt întregi, dar pentru rădăcinile întregi ale metodei este destul de bună.