Metode de optimizare și matematice pentru luarea deciziilor
Dacă funcția obiectiv și sistemul de constrângeri liniare. problema de programare matematică se numește problema programării liniare (ZLP).


Forma de bază a ZLP

Forma ZLP Symmetrical

Problema generală de programare liniară
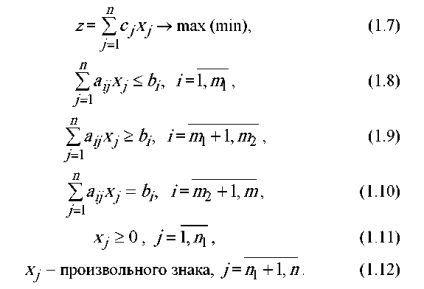
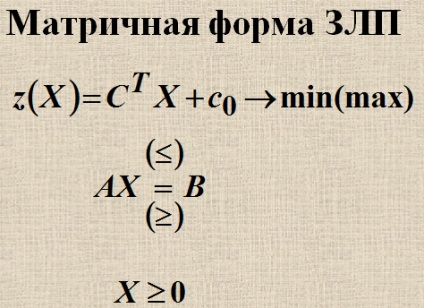
Orice problemă de programare liniară este redusă la standard (canonic) formează principala problemă de programare liniară, care este formulat după cum urmează: a găsi un non-negativ variabile X1, X2, Xn, care satisface constrângerile sub formă de ecuații:
A11X1 + A12X2 + ... + A1nXn = B1;
A21X1 + A22X2 + ... + A2nXn = B2;
Am1X1 + Am2X2 + ... + AmnXn = Bm;
și se referă la maximum a unei funcții liniare a acestor variabile:
E = C1X1 + C2X2 + ... + CnXn Þ max
Se impune, de asemenea, că părțile din dreapta sunt nenegative, adică trebuie îndeplinite condiții:
Reducerea la forma standard este necesară, deoarece de cele mai multe metode de rezolvare a problemelor de programare liniară dezvoltat doar pentru formularul standard. Pentru a aduce la forma standard a problemei de programare liniară poate avea pentru a efectua următoarele etape:
pentru a trece de la minimizarea funcției obiectiv pentru ao maximiza;
schimba semnele cea din dreapta a restricțiilor;
du-te constrângeri privind-inegalitate la egalitate;
a scăpa de variabilele care nu au restricții privind semnul.
Pentru a rezolva problema noastră, vom folosi metoda simplex, deoarece această metodă de rezolvare a problemelor de programare liniară de orice dimensiune.
2) Reducerea problemei generale a LP în forma canonică.
Orice problemă de programare liniară poate fi redusă la o problemă de programare liniară în formă canonică. În acest scop, în general, trebuie să fie în măsură de a reduce problema de maximizare pentru a minimiza problema; trecerea de la constrângeri de inegalitate constrângerilor de egalitate, și înlocuiți variabilele care nu sunt supuse condiției non-negativitate. Maximizarea o funcție echivalentă pentru a minimiza aceeași funcție, luată cu semnul opus, și vice-versa.
De obicei, aduce o problemă de programare liniară în forma canonică este după cum urmează:
în cazul în care problema inițială este de a determina maximul unei funcții liniare, este necesar să se schimbe semnul și să caute minimul acestei funcții;
în cazul în care restricțiile de pe partea dreapta este negativ, ar trebui să fie înmulțită cu -1 această limită;
în cazul în care unele restricții sunt inegalitate, apoi prin introducerea unor variabile suplimentare ne-negative sunt convertite în capitalurile proprii;
Exemplul 1. Reducerea la forma canonică a unei probleme de programare liniară:
Min l = 2x1 + x2 - x3; 2x2 - x3 ≤ 5; x1 + x2 - x3 ≥ -1; 2x1 - x2 ≤ -3; x1 ≤ 0; x2 ≥ 0; x3 ≥ 0.
Introducem fiecare restricții de ecuații nivelare variabilelor de sistem x4, x5, x6. Sistemul ia forma de ecuații, care sunt introduse în partea stângă, în prima și a treia ecuațiile de constrângeri ale sistemului variabilelor x4, x6 cu un „+“, iar al doilea x5 variabilă ecuație este introdusă cu semnul „-“.
Membrii liberi în formă canonică trebuie să fie pozitiv, pentru aceasta ultimele două ecuații, înmulțim cu -1:
Substituind această expresie în constrângerile de sistem și funcția obiectiv și scrierea variabilelor în ordine crescătoare a indicelui, obținem o programare liniară prezentată în formă canonică:
3) Condiția de optimalitate a planului de bază al problemei LP canonice. Metoda Simplex și convergența acesteia.
Metoda simplex este universală, deoarece permite de a rezolva aproape orice problemă de programare liniară, înregistrată sub forma canonică. Ideea simplex a metodei simplex este faptul că, pornind de la unele soluții de referință inițiale, efectuate direcționate secvențial mișcare a soluțiilor optime de susținere a problemei. Valoarea funcției obiectiv în timp ce se deplasează la problemele maxime nu este în scădere.
Deoarece numărul de soluții de referință, desigur, este un număr finit de pași obținem soluția optimă de suport. Soluția de referință se numește o soluție de bază non-negativ.
Algoritmul metodei simplex 1. Modelul matematic al problemei trebuie să fie canonică. În cazul în care este non-canonic, atunci ar trebui să fie redusă la forma canonică. 2. Găsiți soluția de referință originală și testați-l pentru optimalitate. Pentru a completa acest tabel simplex 1. Toate rândurile din tabelul 1 Prima etapă de umplere în funcție de constrângerile de sistem și funcția obiectiv.
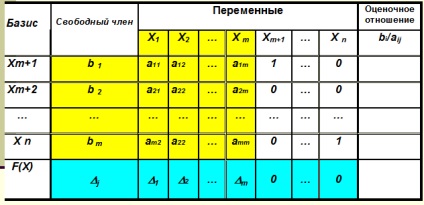
Următoarele cazuri în rezolvarea problemelor la maxim:
1. În cazul în care toți coeficienții ultimului rând al tabelului simplex j 0, apoi a găsit
2 Dacă cel puțin un coeficient j 0, dar variabila corespunzătoare nu este o singură relație de evaluare pozitivă, atunci stația de soluție, Deoarece F (X) , t.e.tselevaya funcția nu este limitată la domeniul soluțiilor fezabile.
În cazul în care cel puțin unul dintre ultimul rând coeficient este negativ, iar în cazul în care variabila corespunzătoare este de cel puțin o atitudine pozitivă estimată. atunci trebuie să pereytik o altă soluție de referință.
4. În cazul în care factorii negativi din numărul ultimul rând, introduceți variabila în coloana bazisnoyperemennoy (PD). ceea ce corespunde cu cel mai mare coeficient velichineotritsatelny absolut.
5. În cazul în care cel puțin un koeffitsientk <0 ,то k- тый столбец принимаем за ведущий.
6. Pentru șirul lider acceptat pe cel care corespunde cu raportul minim de liber membrilor factori pozitivi bi de conducere, K- a coloanei.
7. Un element situat pe linia peresecheniiveduschih și elementul coloană nazyvaetsyaveduschim.
Completați tabelul simplex 2:
umple coloana de bază cu zero-uri și altele
rescrie linia de plumb, împărțind în elementul de conducere
dacă linia de conducere este zero, atunci următorul tabel simplex pot fi transferate la coloanele corespunzătoare
găsi coeficienții rămași conform „dreptunghi“
Vom obține o nouă soluție de referință, care verifica optimalitate:
În cazul în care toți coeficienții ultimului rând j 0, găsit soluția este maximă.
Dacă nu, completați simplex tablou al 8-lea pas, și așa mai departe.
În cazul în care funcția obiectiv F (X) impune găsirea valoarea minimă. criteriul optimalității al problemei este coeficienți jpri vsehj = 1,2.n non-pozitiv.
Convergența metodei simplex. Degenerescenței în problema LP. Cea mai importantă proprietate a oricărui calcul, este convergența algoritmului, adică. E. Posibilitatea aplicării sale în rezultatele dorite (exact un predeterminat-Stu) într-un număr finit de pași (iterații).
Este ușor de observat că problemele cu convergența simplex IU-Toda ar putea apărea potențial la valoarea de decizie r (p. 2 „), într-un caz în care valoarea minimă de aceeași uzură
Acestea vor fi realizate pentru mai multe rânduri de tabel T (q) concomitent-Menno. Apoi, pe următoarea iterație coloanei b (β (q + 1)) va păstra elementele co-zero.