Definiții dependente liniar și sisteme independente de vectori
Să presupunem că avem un sistem de n-vector
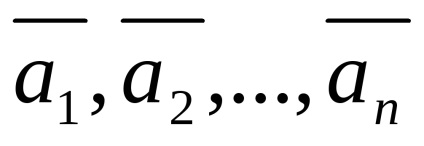
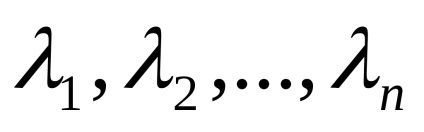
Se numește o combinație liniară de vectori ai sistemului dat, cu un anumit set de coeficienți.
Definiție 23 (prin combinația liniară nulă)
sistem vector
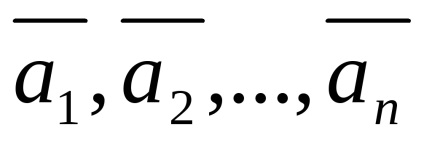
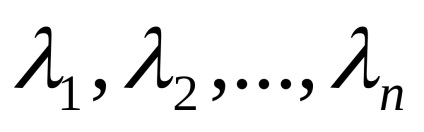
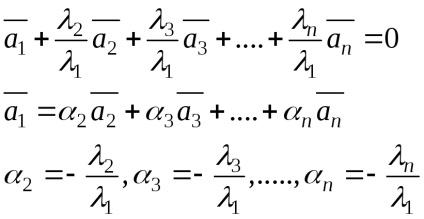
Definiție 24 (printr-o reprezentare vectorială a sistemului ca o combinație liniară a celorlalți)
sistem vector
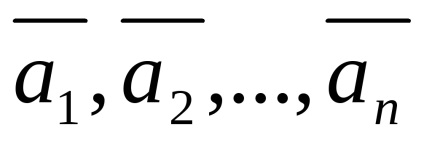
Definiții 23 și 24 sunt echivalente.
Definiție 25 (prin combinația liniară nulă)
sistem vector
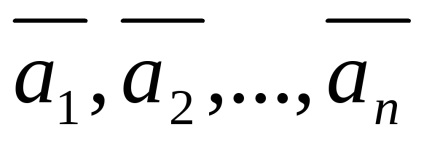
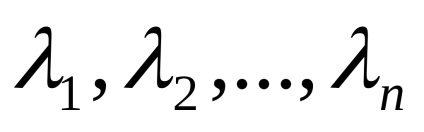
Definiție 26 (prin reprezentări vectoriale ale incapacitatii sistemului ca o combinație liniară a celorlalți)
sistem vector
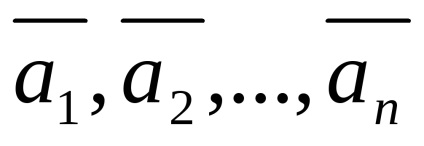
Proprietăți dependente liniar și sisteme independente de vectori
Teorema 2. (vectorul zero în sistemul vector)
Dacă sistemul vector are un vector de zero, sistemul este liniar dependent.
De aceea Obținem liniar dependent de definirea vectorilor prin combinație liniară a unui zero (12), sistemul zavisima. liniar
Teorema3 (sistem vector subsistem dependent)
Dacă sistemul de vectori este un subsistem funcție liniară, întregul sistem este liniar dependent.
Să
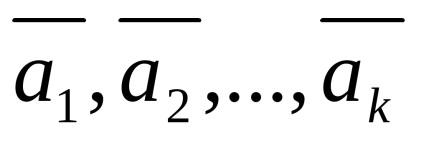
Deci, prin definiție 23, sistemul este liniar dependent.
Orice subsistem sistem liniar independent este liniar independentă.
Dimpotrivă. Lăsați sistemul este liniar independent și are un subsistem dependență liniară. Dar apoi, prin Teorema 3, întregul sistem va fi, de asemenea dependentă liniar. Contradicția. În consecință, sistemul de subsistem liniar independent nu poate fi liniar zavisimoy.
Sensul geometric al dependenței liniare și independența vectorilor
doi vectori

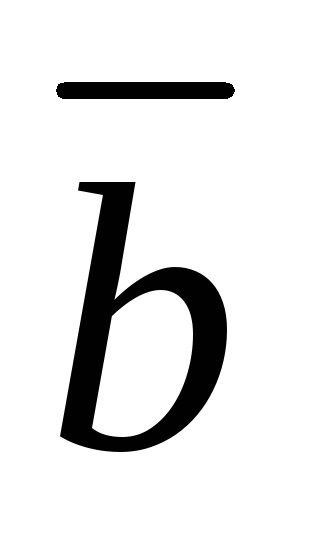
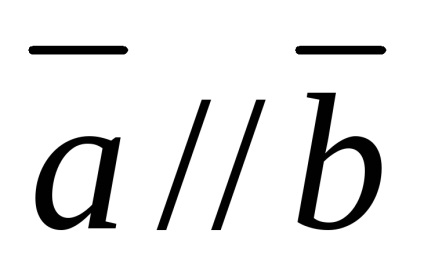

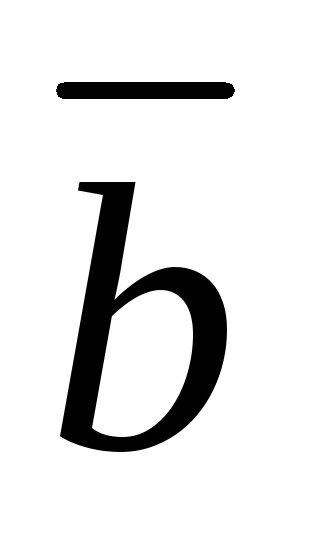
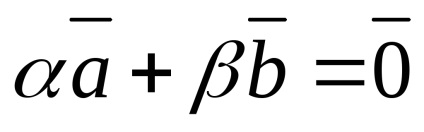
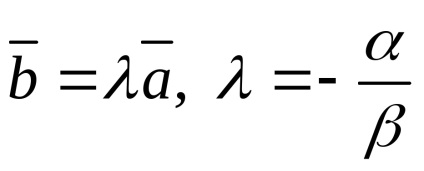
Vectorul de zero este coliniar oricărui vector
Pentru doi vectori sunt liniar independente dacă și numai dacă
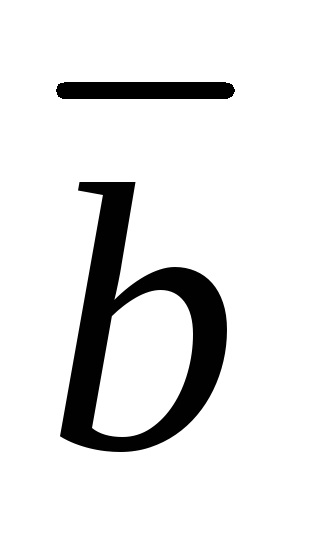

Pentru sistemul de trei vectori este liniar dependent dacă și numai dacă acești vectori sunt coplanari.
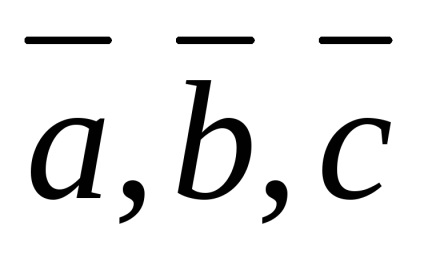
unde
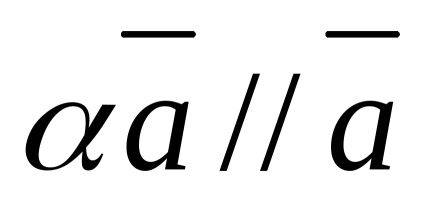
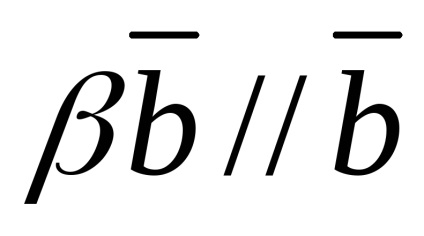
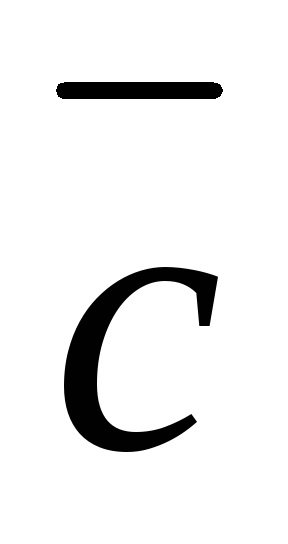
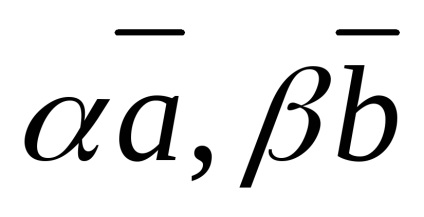
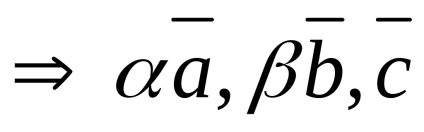
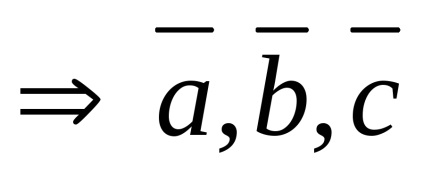
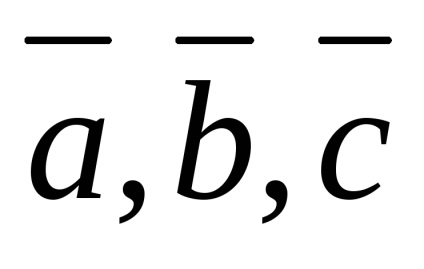
Zero vector coplanar orice pereche de vectori.
Pentru vectori
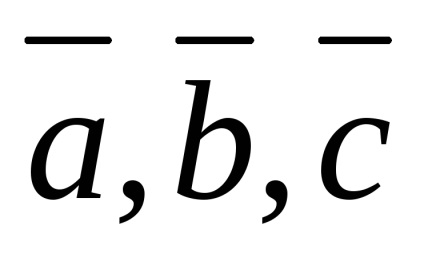
Orice plan vector poate fi reprezentat ca o combinație liniară a oricăror doi vectori noncollinear ai aceluiași plan.
Orice patru vectori în spațiu sunt liniar dependente.
ia în considerare 4 cazuri:
Dacă între vectorii este vectorul zero. Apoi, sistemul este liniar dependent de Teorema 2.
Dacă printre vectorii au cel puțin 1 pereche de vectori coliniare. Apoi, sistemul este liniar dependent de Teorema 5 și 3.
Dacă există între vectorii coplanare triplu de vectori. Apoi, sistemul este liniar dependent de Teorema 6 și 3.
Dacă nu există vectori de zero între vectori coliniar perechi și triplete coplanare. Aplicăm acești vectori la 4 tochkeO.
. Desenează un plan prin vectori. apoi planul vectorilor și planul vectorilor. Apoi, vom trage un plan care trece prin tochkuD perechi paralele de vectori; ; respectiv. Pentru avioanele care traversează liniile de a construi parallelepipedOB1D1C1ABDC.
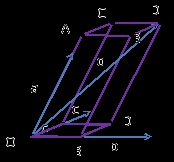
Luați în considerare OB1D1C1 - paralelogram prin construirea regulii paralelogramului.
Luați în considerare OADD1 - paralelogram (proprietăților paralelipipedice) întrucât
Prin Teorema 1
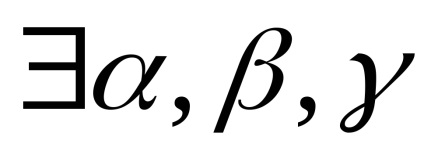
Suma celor trei vectori necoplanare într-un vector, care coincide cu o diagonală a paralelipipedului format de acești trei vectori se aplică la originea comună, cu începutul sumei vectorului coincide cu originea comună a acestor trei vectori.
Dacă spațiul ia trei vector noncoplanar, orice vector al acestui spatiu poate fi descompus într-o combinație liniară a acestor trei vectori.