Definiția 3. Un gradient al unei funcții la un punct este un vector care are coordonate în bază standard. O denumire de gradient mai scurtă (pictograma este citită "nabla").
Definiția 4. Să. Matricea Yakóbi a acestei mapări într-un punct este o matrice constând din derivații fiecărei componente în raport cu fiecare coordonată. Derivatul în raport cu vectorul este definit în același mod ca înainte.
Definiția 5. O mapare se numește diferențiată într-un punct dacă incrementul său total poate fi reprezentat în formă
, unde este un operator liniar, adică o hartă care posedă proprietatea liniarității :. Operatorul acționează din spațiu în spațiu. Se numește cartografia derivată și este notată. Expresia sau se numește diferențial și este notată. Este evident că continuitatea rezultă din diferențiabilitatea.
Teorema 1. (Condiția necesară pentru diferențiabilitate). În cazul în care cartografia este diferențiată la un punct, atunci în acest moment există toate derivatele parțiale și chiar derivații în raport cu orice vector. În acest caz. Cu toate acestea, spre deosebire de cazul funcțiilor unei variabile, existența unui derivat cu privire la orice vector nu implică diferențiabilitatea cartografierii.
Dovada. Lasă-l să fie. atunci
Prin urmare. Absența unei implicații inverse poate fi văzută, de exemplu, din exemplul de mai jos.
Contraexemplu. Lasă-l să fie. Această funcție are un derivat într-un punct de-a lungul oricărui vector și acest derivat este egal cu. Dacă funcția ar putea fi diferențiată la un punct, expresia va depinde liniar de vector. Asta ar fi. Cu toate acestea, nu întotdeauna. De exemplu, sau.
Corolar. Dacă harta este diferențiată într-un punct, atunci toate derivatele parțiale există în acest moment, iar matricea unei liniare
operator în baza standard este matricea Jacobi.
* Dovada. Denumim elementele de matrice în bază. Atunci va fi.
Teorema 2. (O condiție suficientă pentru diferențiabilitate). Dacă toate derivatele parțiale există într-o vecinătate a unui punct și sunt continue în punctul însuși, atunci harta este diferențiată în acest moment.
Dovada. Este suficient, în condițiile indicate, să se demonstreze diferențiabilitatea unei funcții scalare, adică o componentă a cartografierii. Metoda probei este mai ușor de înțeles în cazul. Avem
, unde numărul este cuprins între numere, dar este cuprins între numere (teorema lui Lagrange).
Dacă acestea tind să fie zero, ele tind de asemenea la zero. Folosind continuitatea derivatelor în acest punct, obținem. H, etc.
1 о. Luați în considerare un câmp scalar, adică o funcție. Dacă funcția f este diferențiată într-un punct, atunci, după cum știm deja. În cazul nostru, asta înseamnă că
Deoarece direcțiile cosinilor unui vector sunt egale, vectorul lungimii unității este. Obținem o formulă pentru calculul derivatului direcțional:
Cauza inegalității arată asta. Egalitatea este posibilă numai dacă vectorii sunt coliniari. Astfel, derivatul direcțional are cea mai mare valoare dacă este colinar cu vectorul. Aceasta este și cea mai mare valoare. Prin urmare, rezultă că un gradient poate primi o nouă definiție (fără coordonate).
Definiția. Gradientul unei funcții la un punct este un vector a cărui lungime este egală cu cea mai mare dintre derivați de-a lungul tuturor direcțiilor posibile dintr-un punct. Direcția gradientului coincide cu direcția celei mai rapide creșteri a funcției în acest moment.
Vedem că gradientul unui câmp scalar (funcție) nu depinde de alegerea coordonatelor, ci este determinat de câmpul însuși.
Rețineți că în direcția "minus gradient" funcția scade cel mai rapid, iar în direcții perpendiculare pe gradient, funcția are o rată zero de schimbare, deoarece, dacă, atunci.
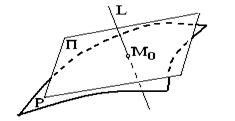
2 о. Considerăm o suprafață definită printr-o ecuație implicită, unde se poate diferenția într-un punct situat pe această suprafață, iar gradientul este nenulos în acest punct (un asemenea punct este numit regulat). Toate liniile drepte care trec prin acest punct și perpendicular pe vector se află într-un plan, care se numește planul tangent la suprafață în punctul respectiv. Ecuația planului tangent are forma
De asemenea, dăm ecuațiile canonice ale normalei (adică, linia care este perpendiculară pe plan și trece și prin punctul):
Fie ca ecuația suprafeței să fie redusă la o formă explicită, unde funcția este diferențiată la un punct. Dacă acceptăm, revenim din nou la ecuație. Acum, prin urmare, ecuația planului tangent ia forma
unde (comparați cu ecuația tangentei cu graficul).
Este clar că atunci când. Astfel, planul tangent în apropierea unui punct este mai aproape de suprafață decât orice alt plan.
Ecuațiile normale iau acum forma
Un exemplu. Scrieți ecuațiile planului tangent și celei normale la elipsoid la un punct.
Soluția. În primul rând, aparține unei suprafețe date, pentru că .
Prima metodă. pentru că , apoi ,. Putem presupune că vectorul normal al planului tangent este egal cu.
Prin urmare, obținem ecuațiile și.
A doua metodă. . În consecință ,,,. Prin urmare, ecuația planului tangent are forma: sau, și ecuațiile canonice ale normalei :.
Exercitarea. Dovediți că ecuația planului tangent la un elipsoid cu ecuația într-un punct situat pe această suprafață are forma.
Generare de pagini în: 0.008 sec.