Moleculele de gaz care se deplasează cu o varietate de viteze, atât magnitudinea și direcția vitezei fiecărei molecule individuale se schimba continuu din cauza coliziunilor (așa cum vom vedea mai târziu, în condiții normale, fiecare moleculă trece printr-o a doua aproximativ 10 coliziuni septembrie).
Deoarece toate direcțiile de mișcare sunt la fel de probabile, distribuția moleculelor de-a lungul direcțiilor va fi uniformă: în orice unghi solid orientat, dar constant, la fiecare moment al timpului direcția de mișcare a unei medii a aceluiași număr de molecule
Situația este diferită de valorile numerice ale vitezei moleculare. Valori posibile. încheiate în limitele de la zero la infinit, nu sunt deloc la fel de probabile. Acest lucru rezultă din următoarele considerații: Schimbarea vitezelor moleculelor în coliziuni are loc la întâmplare. Se poate întâmpla ca o anumită moleculă într-o serie de coliziuni succesive să primească energie de la partenerii săi în coliziuni, ca urmare a cărei energie va depăși în mod semnificativ valoarea medie. Cu toate acestea, chiar dacă ne imaginăm un caz absolut fantastic în care toate moleculele gazului se opresc, transferând energia lor într-o singură moleculă, atunci energia acestei molecule și, în consecință, viteza acesteia vor fi finite. Astfel, viteza moleculelor de gaz, în general, nu poate avea valori, începând cu unele până la. Având în vedere că procesele care ar conduce la o fracție apreciabilă a energiei totale a tuturor moleculelor de pe o moleculă sunt improbabile, se poate argumenta că prea mare comparativ cu viteza medie poate fi realizată extrem de rar. În mod similar, este practic imposibil ca, ca urmare a coliziunilor, viteza moleculei să devină exact zero. În consecință, este foarte mică și foarte mare în comparație cu valoarea medie a vitezei și probabilitatea acestei valori # 965; tinde la zero ca la. așa și când.
Din cele de mai sus rezultă că vitezele moleculelor sunt grupate în principal aproape de o anumită valoare probabilă.
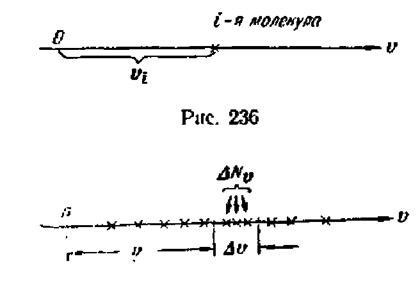
Pentru a clarifica modul în care este posibilă descrierea cantitativă a distribuției moleculelor de către valori # 965; folosim următoarea tehnică vizuală. Vom nota valorile vitezelor pe puncte pe axă # 965; Apoi, la fiecare moleculă pe această axă va corespunde un punct, a cărui distanță față de punctul 0. luată ca origine, este numeric egală cu magnitudinea vitezei moleculei date (Figura 236)
Să presupunem că avem o modalitate de determinare simultană a vitezelor tuturor moleculelor de N dintr-o anumită cantitate de gaz. După desenarea rezultatelor obținute sub formă de puncte [1] pe axă , Obținem o "instantanee" a vitezelor moleculare pentru un anumit timp t (figura 237). Dacă toate valorile # 965;
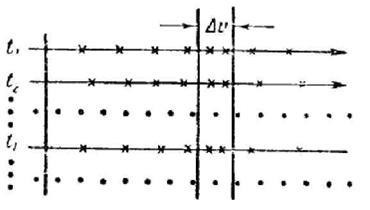
au fost la fel de probabil, punctele ar fi distribuite de-a lungul axei # 965; uniform. Totuși, așa cum am văzut mai sus, vitezele sunt grupate în principal aproape de o anumită valoare probabilă. Aproape zero și valori foarte mari ale vitezei sunt relativ rare. Prin urmare, distribuția punctelor pe axă # 965; va fi inegală, cu o densitate care variază pe diferite secțiuni ale axei.
După ce a determinat densitatea punctelor ca raport al numărului de puncte. care se încadrează în limitele intervalului (figura 237), la mărimea acestui interval:
putem spune că această cantitate este o funcție. De fapt, valoarea lui depinde de locul în axă # 965; se ia un interval, adică de la # 965;
Fiecare act de coliziune între două molecule schimbă aleator poziția punctelor corespunzătoare pe axă # 965; Prin urmare, dacă vom compara un număr de "fotografii" pentru diferite momente de timp: t1. t2, etc. (Figura 238), atunci, în general, pe aceste "fotografii" nu vor exista puncte coincide. Cu toate acestea, dacă gazul este într-o stare de echilibru (adică într-o stare cu parametri nemodificați), atunci distribuția vitezei moleculelor este neschimbată. Prin urmare, densitatea cu care punctele sunt distribuite în diferite părți ale axei # 965; vor fi aceleași pentru toate timpurile.
Dacă luăm mai multe porțiuni de gaz în condiții identice (pentru p și T identice), atunci
distribuția vitezei moleculare în ele va fi, de asemenea, identică. Cu toate acestea, densitatea de puncte pe axa # 965; cu același caracter al distribuției lor de-a lungul axei, este în mod evident proporțional cu numărul considerat de molecule N și, prin urmare, pentru diferite porțiuni ale gazului vor fi diferite. Același lucru pentru porțiuni diferite va fi raportul
dă probabilitatea ca viteza moleculei să aibă o valoare în cadrul dat (situată între # 965; i) din intervalul de viteză (# 965; când servește ca un indice pentru intervalul [2].
preluat de toate intervalele. pe care este posibilă ruperea axei # 965; ar trebui să fie egal cu numărul total de molecule N. Aceasta implică următoarea proprietate a funcției de distribuție;
Ultimul rezultat poate fi explicat și după cum urmează. expresie
Este probabilitatea ca viteza unei molecule să aibă una dintre valorile în intervalul de la 0 la. Întrucât viteza moleculei are în mod necesar o valoare, această probabilitate este probabilitatea unui eveniment fiabil și, prin urmare, este egală cu una. Strict vorbind, condiția (106.4) ar trebui să fie scrisă după cum urmează:
unde A este un factor care nu depinde de # 965 ;, m este masa moleculei, k este constanta Boltzmann.
Caracteristică a funcției de distribuție Maxwell este circumstanța că în exponentul lui e, raportul dintre energia cinetică a moleculei care corespunde vitezei considerate luate cu semnul "-" # 965; la kT. adică o cantitate care caracterizează energia medie a moleculei.
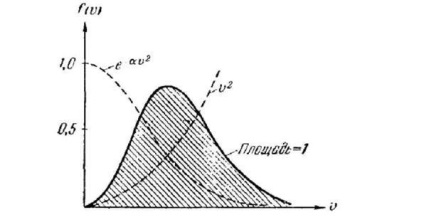
Deoarece factorul de specii cu creștere # 965; scade mai repede decât multiplicatorul, funcția, pornind de la zero (din cauza), atinge un maxim și apoi tinde asimptotic la zero
Condiția (106.5) ne permite să calculam factorul A în (106.6):
Această condiție se numește condiția de normalizare a funcției, iar A este numită factor de normalizare.
Calculele dau pentru A valoarea. Astfel, funcția de distribuție Maxwell are forma
După cum se poate aștepta, forma specifică a funcției depinde de tipul de gaz (de masa moleculei) și de parametrul de stare (la temperatura T). Observăm că presiunea și volumul gazului nu influențează distribuția vitezei moleculelor.
Se poate părea că funcția (106.7) descrie incorect distribuția în legătură cu faptul că ea dispare doar la infinit, în timp ce valorile realizabile ale vitezei sunt limitate de o limită finită. Cu toate acestea, pentru suficient de mari # 965; funcția (106.7) este atât de puțin diferită de zero, încât discrepanța marcată nu are practic nici o semnificație. Viteza corespunzătoare valorii maxime a funcției de distribuție va fi, evident, cea mai probabilă. Într-adevăr, dacă vom compara numărul de molecule ale căror viteze se află în intervale diferite alese de aceeași mărime, atunci cel mai mare va fi intervalul corespunzător situat în vecinătatea maximului. Astfel, rezolvând problema găsirii maximului, găsim viteza cea mai probabilă. Diferențierea (106.6) # 965; și echivalând expresia rezultată la zero, vom avea:
Valorile care satisfac această ecuație corespund minimelor. valoare # 965; expresia de dispariție din paranteze este cea pe care o căutați:
De la interval Vi este mic, viteza fiecăruia dintre ele Moleculele Nvi pot fi considerate aproximativ egale cu cele ale vitezelor aparținând intervalului # 8710; vi. Apoi, suma valorilor vitezelor tuturor moleculelor N poate fi reprezentată în formă. Împărțind această sumă cu numărul de molecule N, obținem [luând în considerare (106.10)] expresia pentru viteza medie:
Trecând de la sumă la integral, descoperim asta
Acest rezultat este de acord cu expresia (99.11) obținută anterior pentru. Pentru a vedea acest lucru, trebuie să înlocuim y în (99.11) până la.
Trebuie remarcat faptul că și.
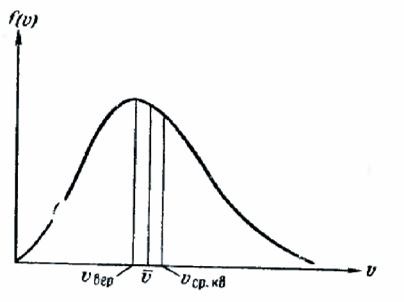
Comparând (106.8), (106.12) și (106.13), se poate observa că. și în același mod depind de temperatura și masa moleculei care diferă doar printr-un factor numeric. Dacă luăm pentru 1, atunci = 1.13, = 1.22 (Figura 241).
Trebuie subliniat încă o dată că legea Maxwell de distribuție a moleculelor în ceea ce privește vitezele și toate consecințele care decurg din aceasta sunt valabile numai pentru un gaz într-o stare de echilibru. Legea este valabilă pentru orice număr N, dacă numai acest număr este suficient de mare. Legea lui Maxwell este statistică, iar legile statisticii sunt mai precise, cu cât sunt aplicate mai mult unui număr mai mare de obiecte identice. Cu un număr mic de obiecte, pot exista abateri semnificative de la previziunile statisticii.
Dacă există un amestec de gaze care este în echilibru, atunci în cadrul moleculelor fiecărui soi există o distribuție (106.7) cu valoarea lui m. Moleculele mai grele se vor mișca în medie cu o viteză mai mică decât cele mai ușoare.
Bazat pe distribuția vitezei moleculelor
putem găsi distribuția moleculelor în funcție de energia cinetică a mișcării translaționale. Pentru a face acest lucru, treceți de la variabila v la variabila # 949; egală cu mv 2/2. Efectuarea substituției u în (106.14). avem
Greutatea moleculară a oxigenului este de 32. În consecință, masa unui kilometru # 956; = 32 kg / kmol. Temperatura camerei este de aproximativ 300 ° K. Înlocuind valorile numerice ale cantităților care intră în ele, obținem în formula numerică (106.17):
Astfel, fiecare moleculă de oxigen trece într-o secundă o cale egală cu o medie de 0,5 km. Deoarece molecula suferă coliziuni foarte frecvente cu alte molecule, această cale constă dintr-un număr mare de segmente rectilinii scurte care formează o linie întreruptă.
Moleculele de hidrogen au o masă de 16 ori mai mică decât moleculele de oxigen, astfel încât viteza lor la aceeași temperatură va fi de 4 ori mai mare și la o temperatură medie de aproximativ 2 km / sec la temperatura camerei.
[1] Rețineți că, petrecând doar o secundă pe fiecare punct, 1012 de ani ar trebui să lucreze la puncte de tragere.
[2] Probabilitatea ca viteza unei molecule să aibă o valoare definită arbitrar # 965; este egal cu zero. Acest lucru se datorează numărului de valori posibile # 965; dar numărul de molecule N este cel puțin mare, dar desigur (comparați cu § 100, textul de la (100.1) la (100.2)).