Dacă Pământul ar fi strict sferic, cu o distribuție uniformă a densității, potențialul gravitațional ar coincide cu potențialul unui punct material a cărui masă este egală cu masa Pământului. În acest caz, satelitul se va deplasa în conformitate cu legile lui Kepler:
legea lui Kepler prima: Orbita satelitului este o a doua curbă de ordin (cerc, elipsa, parabolică), într-unul din focarele care este centrul de masă al corpului atrage.
Sateliții care zboară în jurul Pământului au o orbită eliptică. Ellips- acest locus, suma distanțelor de la fiecare dintre care două puncte numite focare, este o valoare constantă egală cu 2a, unde este axa semimajore a elipsei.
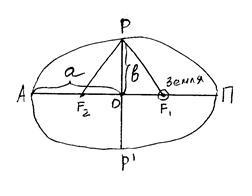
F1 și F2 sunt focarele unei elipse
A-apogee (satelitul are
cea mai mare înălțime deasupra solului)
P-perige (satelitul are
cea mai mică înălțime de deasupra Pământului).
A doua Lege a lui Kepler: vectorul de radius al satelitului pentru intervale egale de timp descrie zone egale. Dacă t1 = t2. apoi S1 = S2. Conform desenului: calea în timp t1 este mai lungă decât timpul t2. prin urmare, viteza satelitului în apropierea perigeului este mai mare decât în apropierea apogeului.
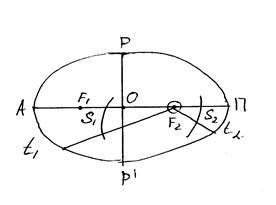
Cifra descrisă de vectorul de rază al satelitului este sectorul. Prin urmare, potrivit celei de-a doua lege a lui Kepler: viteza sectorială a satelitului este constantă.
Legea a treia a lui Kepler. Raportul dintre pătratul perioadei de rotație a satelitului și cubul axei semimajoare a orbitei sale este valoarea constantă:
Dacă presupunem că satelitul se mișcă pe orbită în conformitate cu legile lui Kepler, atunci o astfel de mișcare se numește neperturbată.
În realitate, mișcarea satelitului pe orbită este foarte complicată. Există diferite forțe de perturbare. Mișcarea unui satelit artificial este numită perturbată în acest caz.
Mișcarea neperturbată a sateliților.
Vom presupune că satelitul este un punct material cu masa m. În cazul în care mișcarea netulburată a satelitului, Pământul, de asemenea, luate ca punct de masă de masă M. Având în vedere faptul că m «M, putem presupune că pământul din satelit, practic, atrage adică are o "masă zero".
Pentru a obține ecuațiile diferențiale ale mișcării neperturbate a satelitului, selectați sistemul de coordonate inerțiale (care este fixat în raport cu pământul rotativ).
În cazul în care să ia în considerare efectele altor forțe, în afară de Pământ și interacțiunea prin satelit, producția de ecuații diferențiale ale mișcării satelitului neperturbat, se reduce la rezolvarea așa-numita problemă cu două-corp.
Apoi, neglijând acțiunea satelitului de pe Pământ, să luăm în considerare accelerarea # 969; care stabilește Pământul la satelit din cauza legii gravitației.
Conform celei de-a doua legi a lui Newton:
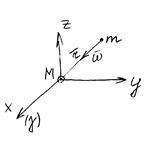
unde forța F este în concordanță
cu legea gravitației:
f este constanta gravitationala
# 964; - vectorul radiației geocentrice a satelitului.
Unde f * M = # 956; - parametrul gravitațional
În ecuația (1) Accelerarea, adică al doilea derivat al căii în timp;
Luați în considerare accelerațiile de-a lungul axelor de coordonate:
; ;
Pentru a găsi aceste cantități, trebuie să înmulțim partea dreaptă a ecuației (1) cu direcțiile cosinus (# 945; - de-a lungul axei OX, - de-a lungul axei OS, # 947; - de-a lungul axei OZ); ; ; atunci
Formulele (2) sunt ecuațiile diferențiale ale mișcării neperturbate a unui satelit artificial.