Descriere bibliografică:
Parametrii primar și secundar și parametrii de transmisie prin cablu influențează reciproc de comunicații definite parametrii geometrici și electrice ale ghidajului mediu. Neavând soluții comune sunt problema estimării capacității de lucru a cablului și permitivitatea echivalent al mediului între cei doi conductori. Soluția la această problemă este relevantă pentru parametrii algoritmice de control automat extrudat izolație poros cu introducerea interloop conexiune oferind un control dinamic efect de compensare eroare unul dintre parametrii (diametru sau permeabilitate izolare dielectrice) într-un parametru de calitate cablu generalizat (capacitate sau impedanță de lucru) prin formarea de proces perturbate circuit de stabilizare automată în al doilea parametru (sau Diamé permitivitate izolație termică) [1].
Se ia în considerare problema determinării parametrilor electrici ai unei perechi răsucite, care formează baza cablurilor de frecvență radio pentru transmisia de date (cablu LAN). În Fig. 1 prezintă o secțiune transversală a unei perechi răsucite neecranate cuprinzând două miezuri ale căror diametre ale izolației sunt diferite.
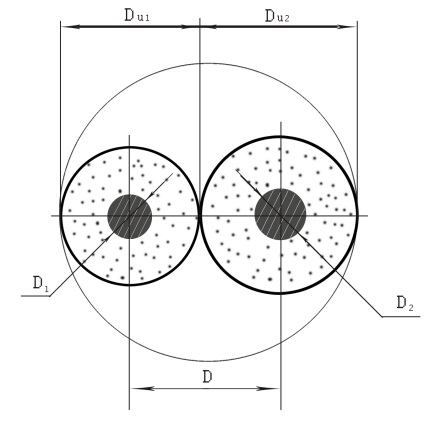
Fig. 1. Secțiunea transversală a cablului LAN
În mod tradițional, permitivitatea echivalentă a mediului de ghidare este estimată ca fiind valoarea medie ponderată a izolației ambelor miezuri, ținând cont de raportul dintre ariile lor transversale. Această estimare este caracterizată de o precizie scăzută, ceea ce este inacceptabil în proiectarea și fabricarea cablurilor cu debit mare. Pentru a estima capacitatea de lucru, ele se opresc în mod tradițional pe formula derivată de VN Kuleshov [2], care se caracterizează și printr-o precizie redusă. Considerăm soluția acestei probleme prin transformările conformale.
Pentru a obține relațiile inițiale care determină procesele din lanțuri, se folosesc parametrii primari ai lanțului. Parametrii R și L sunt reprezentați în circuitul echivalent (Figura 2) prin rezistența longitudinală a lanțului Z = R + jωL. iar parametrii C și G sunt conductivitatea transversală totală a lanțului Y = G + jωC. unde R este rezistența liniară a liniei, L este inductanța liniară, C este capacitatea liniei liniare și G este coeficientul de scurgere.
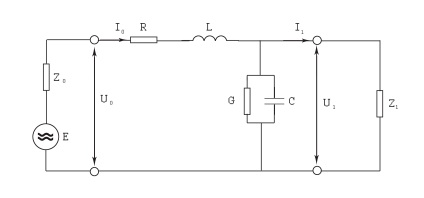
Fig. 2. Circuitul echivalent al liniei de comunicație
Dacă valoarea parametrilor circuitului primar rămân neschimbate pe toată lungimea, un astfel de lanț se numește regulată (uniformă) [3]. Pierderea activă a energiei electromagnetice în timpul propagării sale de-a lungul lanțului datorită R parametrilor primar și G. caracterizează în primul rând pierderile de căldură în conductoarele și alte părți metalice ale sistemului de ghidare (ecran, coajă, armura), al doilea - pierderile în izolație.
Luați în considerare un lanț omogen cu parametrii primari R, L, C, G (Figura 2). Un sistem de ecuații diferențiale care determină tensiunea și curentul în orice punct al lanțului ca o funcție a coordonatei x. are forma [4]:
Acest sistem este valabil pentru orice lanț omogen, indiferent de designul acestuia. Schimbarea în proiectare duce doar la o modificare a valorilor parametrilor primari și secundari, inclusiv rezistența la unde:
Vom considera cablul LAN drept linie fără pierderi. Aceasta înseamnă că considerăm scurgerea egală cu zero (G = 0), adică presupunem că spațiul dintre conductori este neconductiv. În plus, neglijăm pierderile din fire, considerându-le ca fiind conductive ideale (R = 0). Deoarece pentru conductorii ideali inductanța internă este zero, în acest caz inductanța totală a liniei L este redusă la inductanța externă Le. Cu aceste simplificări, formula (2) ia forma:
Pentru a determina capacitatea de lucru, folosim transformarea conformală, folosind funcția liniară fracționată, care are forma [5]:
unde a, b, c, d sunt constante, cu ad-bc ≠ 0. Rezolvarea relației (4) cu privire la z. obținem de asemenea o transformare liniară-fracțională:
O transformare fracțional-liniară are proprietatea ca orice cerc din planul z să treacă într-un cerc pe planul ω și spate, în timp ce linia poate fi considerată ca un cerc cu o rază infinit de mare.
O transformare fracțional-liniară are, de asemenea, o proprietate importantă de conservare a punctelor simetrice: convertește orice pereche de puncte z1 și z2. simetric în raport cu un cerc arbitrar Cz în planul z. într-o pereche de puncte ω1 și ω2. simetric în raport cu imaginea Cω a cercului Cz pe planul ω [5].
Utilizăm proprietatea unei transformări liniare fracționate pentru a păstra cercurile și cartografiem regiunea dintre firele cablului LAN (Figura 3) într-un inel concentric, care este un domeniu simplu dublu conectat.
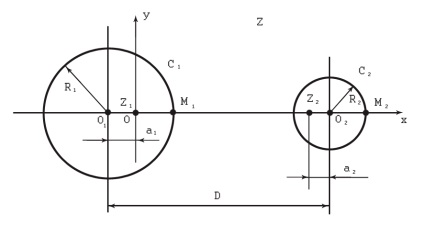
Fig. 3. Interfața cablurilor LAN în planul Z
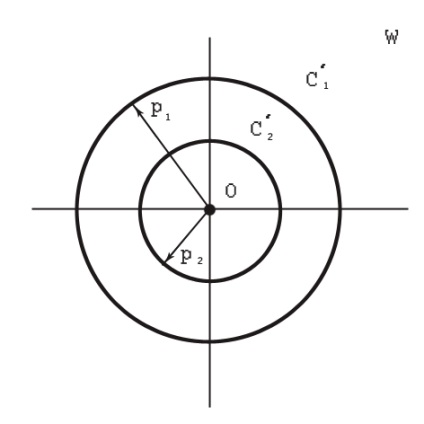
Fig. 4. Interconectarea cablurilor LAN în planul W.
Dacă găsim poziția punctelor z1 și z2. simultan simetric cu privire la ambele date ale cercurilor C1 și C2. care coincid cu suprafețele electrozilor, apoi sub cartografiere
Cercurile C1 și C2 se vor muta în cercurile C'1 și C'2. pentru care punctele ω1 = 0 și ω2 = ∞ vor fi, de asemenea, simetrice. Rezultă că cercurile C'1 și C'2 sunt concentrice, iar centrul lor coincide cu originea în plan ω. care face posibilă determinarea capacității de lucru care apare între miezurile unui cablu LAN, conform formulei cunoscute pentru un condensator sferic (figura 4).
Acum găsim puncte simetrice în ceea ce privește cercurile C1 și C2. Din fig. 3 avem:
unde notația
Plasând originea în punctul simetric Z1. situat în interiorul cercului C1. obținem:
deoarece este ușor să vezi asta
în consecință, funcția ω ia forma:
Având în vedere proprietatea de a menține capacitatea neschimbată în conformitate cu transformările conformale, le găsim în planul ω pentru miezurile cablurilor paralele [5]:
expresia (12) are forma:
Pentru a determina permitivitatea eeq echivalenta, vom folosi din nou maparea conformala, dar acum am mapat planul z (Figura 5) la planul t (Figura 6),
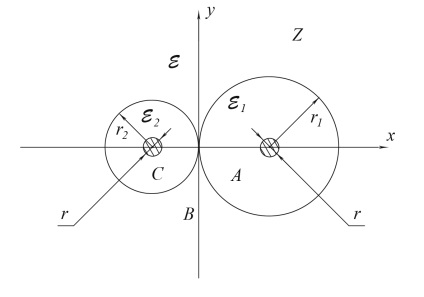
Fig. 5. Interconectarea cablurilor LAN cu izolație în planul Z
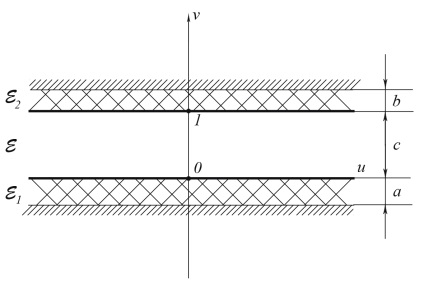
Fig. 6. Rezultatul cartografierii planului z în planul t
Pentru această cartografiere, este necesară îndeplinirea următoarei condiții [5]:
Definim u și v. luând în considerare expresiile (15), (16) și (17):
Afișând planul z pe planul t. am obținut un condensator plat cu plăci infinite. În acest caz este posibil să se determine permitivitatea dielectrică. Aceasta va fi o constantă dielectrică echivalentă necunoscută a mediului între cei doi conductori.
Pentru a rezolva această problemă, condensatorul rezultat poate fi împărțit în trei condensatoare consecutiv condensate cu dielectrice omogene între plăcile lor cu permitivitățile dielectrice corespunzătoare: ε1. e2. ε (figura 7).
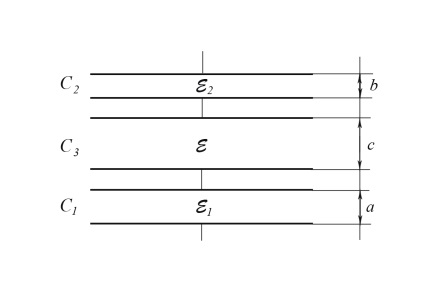
Fig. 7. Circuit echivalent pentru cuplarea a trei condensatoare cu dielectrice omogene între plăcile lor
Situat în Fig. 7 se determină din expresia:
Înlocuind parametrii condensatorilor în expresie (19), obținem:
Din 20 rezultă că:
Capacitorul capacitorului se calculează după formula:
unde l este distanța dintre plăci:
Din expresia (21) introducem variabila m:
Luând în considerare expresiile (21) - (24), obținem:
Rămâne doar să găsim distanțele a, b, c prin definirea coordonatelor punctelor de pe planul t (Figura 6) având coordonatele în planul z (Figura 5):
Folosind expresia (18), obținem coordonatele acestor puncte pe planul t, respectiv:
Substituirea expresiilor (24), (26) - (27) în expresie (25) și ținând seama de faptul că:
unde Di și. Dι1 - diametrul izolației, respectiv, d - diametrul conductorului, obținem:
În (14) înlocuim (28) și ținând seama de faptul că:
Expresia (29) este valabilă și pentru un cablu LAN cu pereche torsadată ecranat, dacă introduceți factorul de screening și factorul de întoarcere.
Mirolyubov, NN Metode de calcul al câmpurilor electrostatice. - M. Nauka, 1963.
Termeni de bază (generați automat). permitivitate, torsadat, capacitate de lucru, izolație permitivitatea dielectrică echivalent cerc C1, C2 circumferința, constanta dielectrică a mediului, permeabilitatea izolației torsionate, parametrii primari, raza C2 cerc, inductanța pe unitatea de lungime, diametrele garniturilor, circumferința interioară S1'opredelim, parametrii torsadat echivalent cablu capacitate dielectrică de lucru, caracteristicile electrice ale ghidului, cabluri de conectare, capacitate de lucru.