Prezentare pentru lecție
Scopul lecției:- repeta construirea de grafice de funcții care conțin semnul modulului;
- să se familiarizeze cu o nouă metodă de plotare a unui grafic al unei funcții de element liniar;
- stabili o nouă metodă pentru rezolvarea problemelor.
Pe diapozitivul 1 al prezentării.
Care este graficul funcției y = | x |. (diapozitivul 2).
(un set de bisectoare cu unghiuri de coordonate 1 și 2)
Găsiți corespondența dintre funcții și grafice, explicați alegerea dvs. (diapozitivul 3).
Elev: să construiți un grafic al acestei funcții de care aveți nevoie
- construi o parabolă y = x 2 -2x-3
- o parte a graficului peste OX este reținută și o parte a graficului de mai jos OX este afișată simetric în jurul axei OX (diapozitivul 5)
Student: Pentru a construi un grafic al acestei funcții, aveți nevoie de:
- o parte a graficului pentru x 0 este stocată și simetriile sunt afișate în raport cu axa OY (diapozitivul 7)
Student: Pentru a construi un grafic al acestei funcții, aveți nevoie de:
- Este necesară construirea unei parabole y = x 2 -2x-3
- construim y = x 2 -2 | x | -3; stocăm partea graficului și o mapăm simetric pe OC
- partea deasupra lui OX este păstrată, iar partea inferioară este mapată simetric în raport cu OX (diapozitivul 9)
Următoarea sarcină se face în scris în cărți de scris.
1. Construiți un grafic al funcției elementului liniar y = | x + 2 | + | x-1 | - | x-3 |
- găsim zerourile expresiilor submodulului x1 = -2, x2 = 1, x3 = 3
- sparge axa în goluri
- pentru fiecare interval pe care îl scriem
la -2 x<1, у=х
la 1 x<3, у = 3х-2
- compunem funcția liniară-piesă.
Am construit un grafic de funcții utilizând definiția modulului (diapozitivul 10).
Vă aduc la cunoștință "metoda de vârf", care vă permite să construiți un grafic al funcției piesă liniară (diapozitivul 11). Algoritmul pentru construirea copiilor este scris într-un notebook.
algoritm:- Noi găsim zerourile fiecărei expresii de submodule
- Noi compunem un tabel în care, pe lângă zerouri, scriem o valoare a argumentului în stânga și în dreapta
- Punem punctele pe planul de coordonate și conectăm în serie
2. Să analizăm această metodă pe aceeași funcție y = | x + 2 | + | x-1 | - | x-3 |
Profesorul se află pe tablă, copiii se află în notebook-uri.
- găsim zerourile fiecărei expresii de submodule;
- compilam o tabelă în care, pe lângă zerouri, notăm o valoare a argumentului din stânga și din dreapta
- Punem punctele pe planul de coordonate și conectăm în serie.
Graficul grafic al unei funcții lineare pe bucăți este o linie întreruptă cu legături extreme infinite (diapozitivul 12).
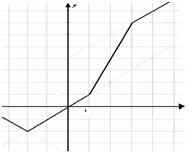
Cum se obține graficul mai rapid și mai ușor?
3. Pentru a stabili această metodă, propun următoarea sarcină:
Pentru ce valori ale lui x face funcția y = | x-2 | - | x + 1 | își asumă cea mai mare valoare.
Urmăm algoritmul; elev pe tablă.
y (3) = 1-4 = 3, conectăm punctele succesiv.
4. Sarcina suplimentară
Pentru ce valori a face ecuația || 4 + x | - | x-2 || = a are două rădăcini.
a) Pentru ce valori ale lui X face funcția y = | 2x + 3 | +3 | x-1 | - | x + 2 | are cea mai mică valoare.
b) Construiți un grafic al funcției y = || x-1 | -2 | -3 | .