Titlul lucrării: Desenarea graficelor în mediul de programare MATLAB
Domeniu: Informatică, Cibernetică și Programare
Descriere: Scopul lucrării: de a învăța cum să construiți grafică de diferite tipuri în mediul software MATLAB. Pentru a studia operatorii de bază de plotare în mediul de programare MATLAB; stăpânește principiile construirii diferitelor tipuri de grafice în mediul de programare MATLAB.
Mărime fișier: 354.21 KB
Lucrarea a fost descărcată: 31 de persoane.
Ministerul Educației și Științei al Federației Ruse
FGAOU VPO "Belgorod State National
Universitatea de cercetare "(NIU" BelGU ")
FACULTATEA DE ȘTIINȚĂ A COMPUTERULUI ȘI TELECOMUNICAȚII
DEPARTAMENTUL DE SISTEME ȘI TEHNOLOGII DE INFORMARE ȘI TELECOMUNICAȚII
Raport privind activitatea de laborator №1
Pe disciplina informatică
Tema lucrării "Crearea de grafice în mediul de programare MATLAB"
student al grupului 141206
Petriv Andrey Vladimirovich
Ph.D. Profesor asociat Prokhorenko Ekaterina Ivanovna
Obiectiv: învățați cum să construiți grafică de diferite tipuri în mediul software MATLAB.
1) să studieze operatorii de bază ai diagramelor în mediul de programare MATLAB;
2) să stăpânească principiile construirii diferitelor tipuri de grafice în mediul de programare MATLAB.
Date individuale pentru performanța muncii
(opțiunea numărul 17)
Sarcina 1. Construiți un grafic de funcții.
Variabilele utilizate pentru a construi algoritmul:
k - valoarea inițială a lui x
k 2 este valoarea finală a lui x
n este numărul de valori
e - pas (distanța dintre două valori ale lui x)
Schema de diagramă pentru o sarcină este prezentată în figura 1.
Figura 1.
Lista 1 este o implementare a algoritmului în sistemul MatLab.
k 1 = intrare ("introduceți numărul");
k 2 = intrare ("introduceți numărul");
n = intrare ("introduceți numărul");
Funcțiile standard sunt utilizate aici
intrare - introducere de date
figura (1), plot (x y.) - un grafic netedă a funcției y (x), dimensiunea vectorilor construite în fereastra grafică 1 ar trebui să fie aceeași
Testarea algoritmului:
Pentru k1 = 0; k2 = 1; n = 100 graficul este ramura hiperboliei prezentată în Figura 2.
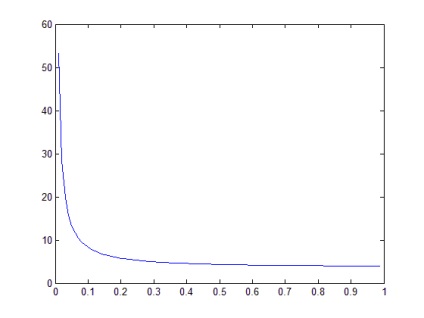
Concluzie: acest algoritm ne permite să construim un grafic al funcției din punctele date.
Ținta 2. În același grafic pentru a construi trei curbe: care corespunde primului termen (roșu linie punctată) corespunzătoare doilea termen (tip punct-liniuță linia verde) care corespunde rezultatului plus (negru solide) (3 cicluri).
Variabilele utilizate pentru a construi algoritmul:
k - valoarea inițială a lui x
k 2 este valoarea finală a lui x
n este numărul de valori
e - pas (distanța dintre două valori ale lui x)
y2 (i) # 150; sin 3 x
y3 (i) # 150; suma y1 (i), y2 (i) și 5. ()
Schema tehnologică pentru 2 sarcini este prezentată în figura 3.
Figura 3.
Listingul 2 este o implementare a algoritmului în sistemul MatLab.
Funcțiile standard sunt folosite aici:
intrare - introducere de date
figura (1); țineți-vă; țineți-l # 150; în fereastra grafică 1, sunt construite trei grafice de funcții.
parcela (x, y 1, '- r') - în fereastra grafică 1 este construit un grafic neted al funcției y (x): o linie roșie punctată fără marcator
plot (. x y 2 '-. g') - în fereastra grafică 1 este construit grafic funcție netedă y (x): verde linie tip dot-liniuță
(x, y 3, '- k') - în fereastra grafică 1 este construit un grafic neted al funcției y (x): o linie neagră solidă fără un marker
Testarea algoritmului:
Pentru k1 = 0; k2 = 2 * pi; n = 500 graficul este prezentat în figura 4.
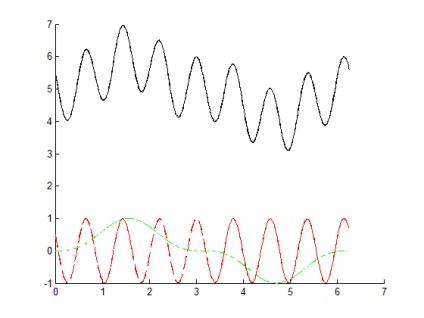
Concluzie: acest algoritm este eficient și permite o fereastră grafică unică pentru a plasa 3 grafice izolate în felul lor (linia roșie punctată fără punct-la-bord linia de solid negru marcator linie verde fara semnul ..).
Sarcina 3. Construiți o curbă y (x) conform unei reprezentări date.
Epicicloidă x = (a + b) cos t - un cos ((a + b) t / a), y = (a + b) sin t - un păcat ((a + b) t / a). t = [0,2 π) pentru un> 0. b> 0, b / a # 150; este un număr întreg.
solid galben cu marcator de tip cerc
Un epicicloid este o curbă plat. formată de un punct fix al cercului. rularea la exteriorul celeilalte circumferințe fără alunecare.
Variabilele utilizate pentru a construi algoritmul:
a este un număr mai mic sau egal cu b (raza unui cerc mai mic)
b este un număr întreg (raza unui cerc mai mare)
t 1 - valoarea inițială
t 2-valoarea finală
Schema de evoluție a acestui algoritm este prezentată în figura 5.
Listingul 2 este o implementare a algoritmului în sistemul MatLab.
a = intrare ("introduceți numărul");
b = intrare ("introduceți numărul");
n = intrare ("introduceți numărul");
Funcțiile standard sunt folosite aici:
intrare - introducere de date
plot (x .. y „- oy“) - în fereastra grafică 1 este construit grafic neted al funcției y (x): o linie de solid galben cu un marker, cum ar fi un cerc
Testarea algoritmului:
Pentru a = 5; b = 10; n = 500 Graficul este prezentat în figura 6 (curba fără discontinuitate).
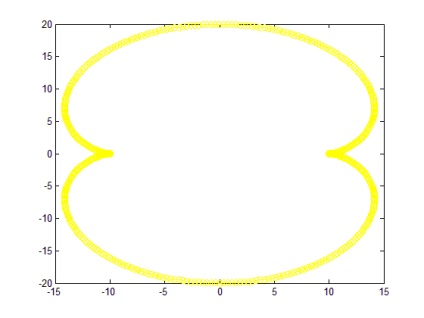
Când a și b se schimbă. de exemplu, pentru a = 2; b = 100 graficul este modificat și are forma prezentată în Figura 7.
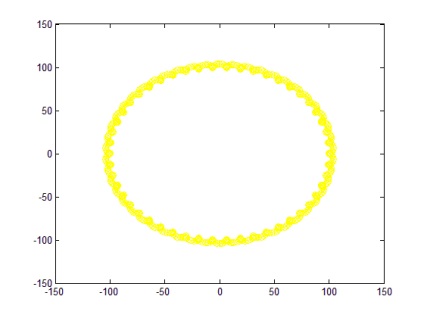
Dacă cerințele nu sunt îndeplinite, la a = 5; b = 17; n = 500 graficul are forma unei curbe cu o pauză (Figura 8).
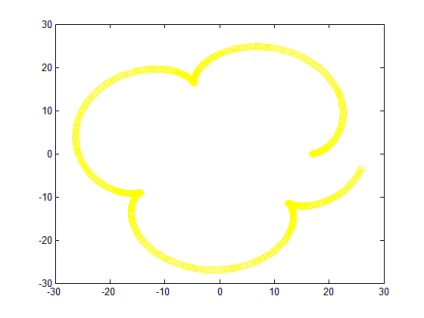
Concluzie: Algoritmul activ permite o curba y (x) pentru o anumită prezentare, funcția program depinde în primul rând de valorile a și b. care trebuie să satisfacă condiția b / a = un număr întreg.
Comentariile profesorului
Infracțiunea administrativă ca bază pentru răspunderea administrativă. Procedura privind cazurile de încălcare a normelor administrative în domeniul activității de întreprinzător. Caracteristicile materiale și procedurale ale procedurilor în cazurile de încălcare a normelor administrative în domeniul activității de întreprinzător.