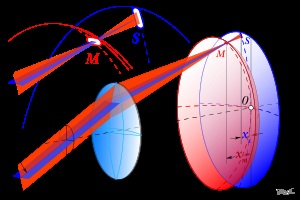
Astigmatismul unei raze înclinate de raze.
M este suprafața focală meridională.
S este suprafața focală sagitală.
Astigmatismul este o aberație. la care imaginea unui punct situat în afara axei și formată de un fascicul îngust de raze. reprezintă două segmente drepte perpendiculare una la cealaltă la distanțe diferite față de planul focarului fără aberație (planul Gauss) [1]. Astigmatismul apare deoarece razele de fascicul înclinate au diferit punctul de convergență - punctul meridian sau sagital fascicul oblic focare infinit de subțire.
Astigmatismul se explică prin dependența de unghiurile de refracție ale razei fasciculului pe unghiurile incidenței acestora. [P 1] Deoarece grinzile individuale înclinate incidente fasciculului pe suprafața refracting la unghiuri diferite, apoi refractate la unghiuri diferite se intersectează la distanțe diferite de la suprafața refractie. Mai mult decât atât, este posibil să se găsească o poziție pentru suprafața imaginii, când toate razele fasciculului situate într-una dintre avioane (meridionali sau sagital) [P 2] se intersectează la suprafața menționată. Astfel, grinda astigmatism formează un punct de imagine sub forma a două linii focale astigmatism pe suprafețele focale respective, care au forma unor suprafețe de rotație a curbelor cu diferiți parametri, și sunt legate una de alta la axa sistemului.
În cazul în care poziția acestor suprafețe pentru anumite domenii de puncte nu se potrivesc, atunci aceasta indică prezența astigmatism, înțelegere astigmatism această diferență între focarele sagital și Meridionale.
În acest caz, în cazul în care sunt situate focii meridionale mai aproape de suprafața de refracție decât sagital, atunci vorbim despre astigmatismul pozitiv, și în cazul în care mai mult, atunci negativ. În cazul coincidenței suprafețelor focale, diferența astigmatică este zero, fasciculul astigmatic degenerează într-unul homocentric. Cifra de scatter merge într-un punct, iar curbura suprafeței rezultate va determina curbura câmpului de imagine.
În teoria aberațiilor din a treia ordine, astigmatismul este caracterizat prin a treia sumă (coeficientul) Sieil (SIII) și este considerat împreună cu curbura suprafeței imaginii. caracterizat prin a patra sumă a lui Seidel (SIV). O asemenea considerație comună se datorează dependenței manifestărilor acestor aberații.
Mai mult, formulele prin care se determină focarele astigmatice includ ambii acești coeficienți. De exemplu, componenta meridională x m ''> pentru un anumit punct de imagine situat la înălțimea l 'poate fi definită ca
unde f 'este lungimea focală a sistemului.
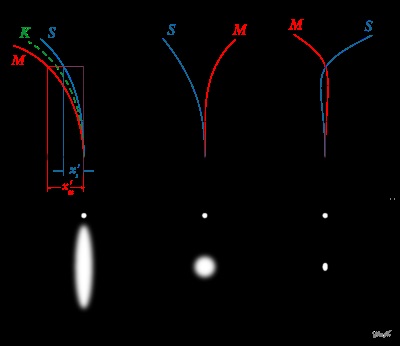
Câteva exemple de grafice de astigmatism și modelele lor de împrăștiere corespunzătoare, pentru raze axiale și oblice (25 °) de raze:
1. - lentilă unică biconvexă,
2. - o lentilă simetrică de tip aplanat,
3. Anastigmat (Tessar).
Reprezentarea grafică a astigmatismului
Astigmatismul sistemului optic este deseori descris grafic - pe baza calculului pozițiilor focarelor astigmatice ale grinzilor elementare. de stabilire a unghiurilor de înclinare a razei principale de-a lungul axei ordonate și a distanței focarelor astigmatice de planul Gauss [2] de-a lungul axei abscise.
Curbele obținute ne permit să judecăm forma suprafețelor focale astigmatice și, pe această bază, despre unele caracteristici ale sistemului investigat.
De exemplu, astigmatismului semn pozitiv corespunde, de obicei, în cazul în care sistemul, de asemenea, are o curbură și suprafața imaginii (adică ultima suprafață situată între cele două suprafețe de astigmatism) focare. În acest caz, figura împrăștiată pentru punctul periferic al unui obiect plat va fi oval neclară. Concentrarea simultană pe toate punctele unui obiect plat pentru un astfel de sistem va fi imposibilă.
Astigmatismul negativ semnificativ permite "combinarea" suprafeței imaginii cu planul Gaussian. Cu toate acestea, datorită faptului că punctele periferice ale unui obiect plat sunt reprezentate de grinzi insuficient de focalizate, o imagine clară a punctelor unui astfel de obiect va fi posibilă numai în centrul câmpului.
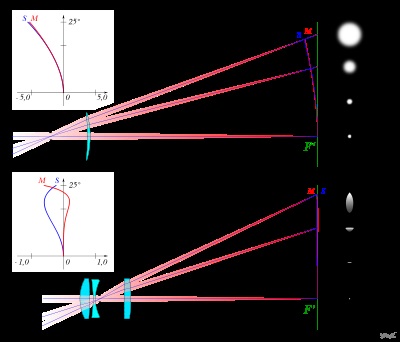
Astigmatism corectat pentru diferite tipuri de lentile (monoclu condițional și triplet). Diagrama arată, de asemenea, modul în care magnitudinea astigmatismului depinde de unghiul de transmisie al razelor luminoase prin obiectiv
Din moment ce astigmatismul este inerent nu numai în razele largi, dar și în cele subțiri (elementare) ale razelor, diafragma nu afectează în nici un fel magnitudinea. Prin urmare, ca și alte aberații, astigmatismul este corectat prin selectarea curburii suprafețelor și a grosimii componentelor optice, precum și a golurilor de aer dintre ele.
Un exemplu de lentilă simplă. cu astigmatism corectat, va exista o lentilă a monocluului de tip Wallographic. unde este îndreptată de diafragma de deschidere. razele inclinate raspund suprafetelor lentilelor meniscus la unghiuri mici fata de cele normale. În acest caz, astigmatismul pozitiv al spate (convexă) suprafața meniscului este atât de mic încât poate fi compensată prin fața astigmatismului negativ de suprafață (concavă).
Cu toate acestea, în acest caz, chiar și cu eliminarea completă a astigmatismului, curbura suprafeței imaginii este mare. Astfel, astigmatismul corectat nu garantează încă claritate pe tot cuprinsul câmpului imaginii.
Prin urmare, atunci când se calculează așa-numitele anastigmatici, se folosesc soluții mai complicate, care permit să se corecteze, într-un anumit unghi, ambele aberații. Și, de regulă, chiar astigmatismul corectat are o mică valoare negativă, cu atât mai mic este unghiul de vedere al lentilei.
Astigmatismul unui sistem care nu are simetrie centrală
Pentru sistemele optice, care nu au simetrie centrală, astigmatismul se poate baza pe o suprafață de curbură diferită de refracție în Meridional și secțiuni transversale sagital.
Un caz special al fasciculului astigmatic format de un astfel de sistem este un fascicul format dintr-o lentilă cilindrică pozitivă, o imagine a căreia este pe un segment de linie dreaptă și cealaltă în infinit.
- ↑ Conform celei de-a patra lege a opticii geometrice. Raportul sinusului dintre unghiul de incidență și sinusul unghiului de refracție este o valoare constantă și este egal cu raportul invers al indicilor de refracție ai mediei. păcatul i sin i '= n' n> = >>
- ↑ În sistemele optice cu un plan meridian central de simetrie. va fi orice plan la care aparține axa optică a sistemului. De exemplu, practic toate imaginile schemelor optice ale obiectivelor fotografice sunt doar secțiuni transversale meridionale. În literatura optică europeană și americană, acest avion este adesea denumit tangențial.
Planul Sagittal. pentru orice fascicul de raze situate în planul meridian, va exista un plan care include raza principală a acestui fascicul și perpendicular pe planul meridional.
Într-o sisteme optice simetrice axial astfel de diviziune este important să se evalueze proprietățile în afara axei și / sau raze înclinate, deși nu poate avea sens să fascicul dispuse direct pe axa optică
- E. A. Iofis. Tehnologie fotografică / I. Yu Shebalin. - M. "Enciclopedia sovietică", 1981. - P. 28, 29. - 447 p.
- DS Volosov. Capitolul II. Aberația optică a lentilelor // Optica fotografică. - ed. 2 - M. "Art", 1978. - P. 91-234. - 543 p.
- Begunov BN Geometric optics. - M. Izd-vo MGU, 1966.
- Rusinov, M. M. Optica tehnică. - L. Inginerie mecanică, 1979.
- Slyusarev G. G. Calculul sistemelor optice. - L. Inginerie mecanică, 1975.