O fracțiune compusă este o fracțiune care are o fracțiune în numărător sau în numitor sau atât în numărător, cât și în numitor. Din acest motiv, fracțiunile compuse sunt numite și fracțiuni cu mai multe etaje. Procesul de simplificare a fracțiunilor compuse variază de la simplu la complex, în funcție de numărul de termeni din numărător și de numitor sau de prezența variabilelor în numerotator și în numitor.
Etapele Editare
Metoda 1 din 2:
Simplificarea fracțiunilor compuse prin înmulțirea cu valoarea reciprocă Editați
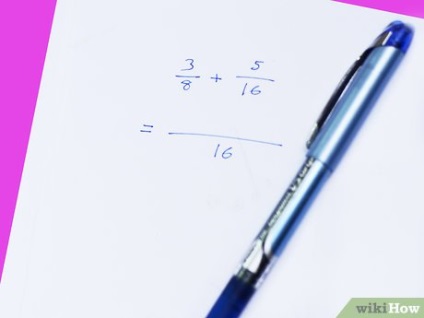
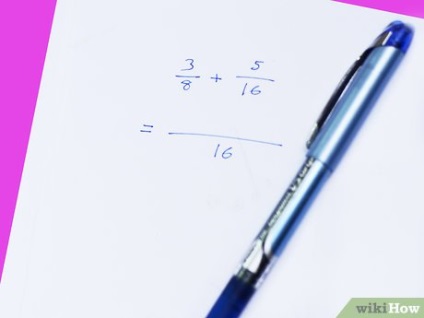
- De exemplu, o fracție compusă este dată: (3/5 + 2/15) / (5/7 - 3/10). În primul rând, simplificăm atât numerotatorul, cât și numitorul acestei fracțiuni, la o fracțiune.
- Pentru fracțiuni în numărător, NOx = 15. Prin urmare, dăm fracțiunea 3/5 la numitorul comun: 3/5 * 3/3 = 9/15. Rescriim numerotatorul ca: 9/15 + 2/15 = 11/15.
- Pentru fracțiunile din numitor, NOx = 70. Prin urmare, dăm ambele fracțiuni numitorului comun: 5/7 * 10/10 = 50/70 și 3/10 * 7/7 = 21/70. Rescriem numitorul ca: 50/70 - 21/70 = 29/70.
- Astfel, rescriim fracțiunea compusă ca: (11/15) / (29/70).


- În exemplul nostru, fracțiunea din numitor este de 29/70. Înapoi fracțiunea este 70/29.
- Rețineți că dacă există un număr întreg în numitorul unei fracții compuse, atunci reciprocitatea acesteia este aceeași. De exemplu, dacă o fracție compusă (11/15) / (29) este dată, atunci reciproca întregului 29 (poate fi scrisă ca fracție 29/1) este o fracție 1/29.


- În exemplul nostru: 11/15 * 70/29. 11 * 70 = 770 și 15 * 29 = 435. Deci rezultatul multiplicării este de 770/435.
- În exemplul nostru, GCD = 5. Astfel, 770/5 = 154 și 435/5 = 87. Fracțiunea simplificată (și răspunsul final): 154/87.


- De exemplu, fracțiunea compus (1 / x) / (x / 6) poate fi ușor simplificată prin înmulțirea cu cantitatea reciprocă: (1 / x) * (6 / x) = 6 / x 2.
- Un alt exemplu: fracțiunea ((1) / (x + 3)) + x - 10) / (x +4 + ((1) / (x - 5))) este dificil de simplificat prin înmulțirea cu valoarea reciprocă. Adică expresiile în numărător și în numitor vor fi dificil de simplificat până la o fracțiune. Prin urmare, utilizați metodele de simplificare descrise mai jos.


- Este mai ușor de înțeles prin exemplu. Să încercăm să simplificăm fracțiunea compusului: ((1) / (x + 3)) + x - 10) / (x +4 + ((1) / (x - 5))). În această fracțiune compusă există fracțiuni (1) / (x +3) și (1) / (x-5). Cel mai mic numitor comun (NOR) este (x +3) (x-5).
- În exemplul nostru, înmulțiți fracțiunea compusului (((1) / (x +3)) + x - 10) / (x +4 + ((1) / (x - 5) x-5) / / (x +3) (x-5)).
- Înmulțiți numărul: (((1) / (x + 3)) + x - 10) x (x + 3)
- = (((x + 3) (x-5) / x + 3) + x (x + 3) (x-5)
- = (x-5) + (x (x 2 - 2 x 15)) - (10 (x 2 - 2 x 15))
- = (x-5) + (x3-2x2 -15x) - (10x2-20x150)
- = (x-5) + x 3 - 12 x 2 + 5x + 150
- = x 3 - 12x 2 + 6x + 145
- Înmulțiți numitorul: (x +4 + ((1) / (x - 5))) x (x + 3) (x-5)
- = x (x + 3) (x-5)) + 4 ((x + 3) (x-5)) + (1 / (x-5)) (x + 3) (x-5).
- = x (x 2 - 2x - 15) + 4 (x 2 - 2x - 15) + ((x + 3)
- = x 3 - 2x 2 - 15x + 4x 2 - 8x - 60 + (x + 3)
- = x 3 + 2x 2 - 23 x - 60 + (x + 3)
- = x 3 + 2x 2 - 22 x 57


- Deci, în numerotator se scrie expresia: x 3 - 12x 2 + 6x + 145, iar în numitor - expresia: x 3 + 2x 2 - 22x - 57. Fragment simplificat: (x 3 - 12x 2 + 6x + 145) / 3 + 2 x 2 - 22x - 57)