Sensul geometric al derivatului 1
Sensul fizic și economic al derivatului 2
Diferentibilitatea functiei 3
Schema de calcul a derivatului S
Reguli de bază ale diferențierii 5
Derivații de funcții elementare fundamentale 6
Instrumente derivate de ordin mai mare 7
Elasticitatea funcției 8
Teoreme de bază privind funcțiile diferențiate și aplicațiile lor 9
Extrema funcției 13
Convexitatea funcției 16
Asimptote ale graficului funcției 19
Diferențial de funcție 22
Aplicarea diferenței în calcule aproximative 24
Conceptul diferențelor de ordin superior 25
Fie funcția y = f (x) definită pe intervalul X. Luăm un punct x € X. Fie x un increment de x0, atunci funcția va primi incrementul y = f (x + x) -f (x).
Derivata funcției y = f (x) se numește limita raportul funcției increment la incrementarea argumentul atunci când acesta din urmă tinde la zero (dacă există această limită):.
De asemenea, derivatul este notat cu y 'anddy / dx.
Semnificația geometrică a derivatului
Pentru a înțelege semnificația geometrică a derivatului, considerăm problema tangentă.
Considerăm în plan graficul funcției continue y = f (x) (vezi Figura 3.1).
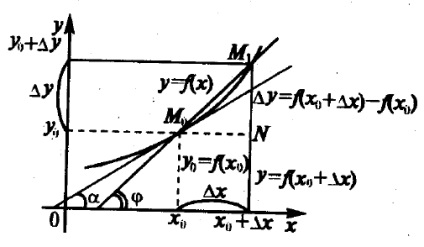
Să construim tangenta acestei curbe la punctul M0 (x0, y0). În primul rând, este necesar să definim conceptul de tangentă. Pentru acest argument vom da x0 priraschenieh și treci pe curba y = f (x) din punctul M0 (x0, f (x0)) la punctul M1 (x0 + h, f (x0 + h)). Desenăm secțiunea M0 M1. Subtangent la curba y = f (x) realizează poziția limită a aproximarea secantă M0 M1 M1 la un punct la punct M0. și anume prih0.
tăiere Corner factor M0 M1 (uglanaklona tan această linie la abscisă) poate fi găsit izM0 M1 N:
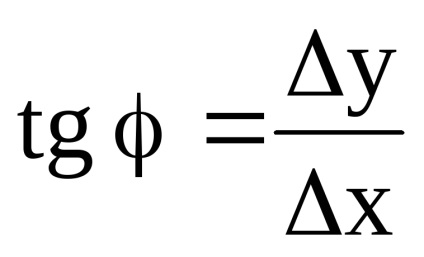
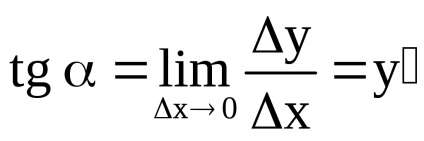
Astfel, derivatul funcției este tangenta pantei tangentei la graficul funcției pe axa abscisă (panta tangentei).
Sensul fizic și economic al derivatului
Luați în considerare o mișcare rectilinie conform legii s = s (t), unde s este calea traversată și t este timpul. Este necesar să găsim viteza mișcării la momentul t0.
Pentru intervalul ttc al timpului t0, distanța s = s (t0 + t) -s (t0) va fi traversată. Apoi, viteza medie pentru acest interval de timp va fi s / Δt. Cu cât intervalul T este mai mic, cu atât mai bine acest raport va evalua viteza la momentul t0:
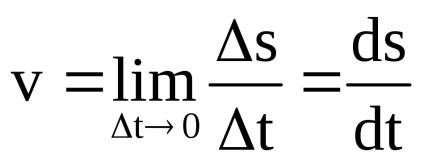
Astfel, derivatul unei funcții este rata de schimbare a valorii unei funcții într-un punct. Acest sentiment al derivatului este convenabil să se folosească nu numai în fizică, ci și în economie.
De exemplu, în cazul în care funcția p = p (q) exprimă dependența producției de produktsiiq pribylipot, arată o creștere derivat de profit marginal (rata profitului schimbare la schimbarea producției):
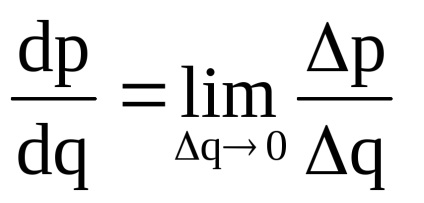
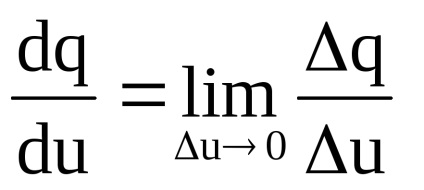
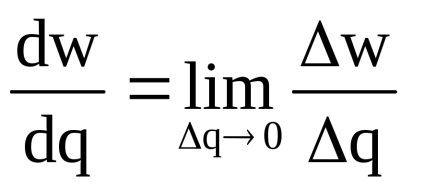
Pe baza conceptului de derivat în economie, se calculează venitul marginal, venitul marginal, produsul marginal, utilitatea marginală, productivitatea marginală și alte valori limită.
Valorile limită caracterizează procesul de schimbare a entității economice. Astfel, derivatul acționează ca rata de schimbare a unui obiect economic (proces) în timp sau relativ la un alt factor investigat.