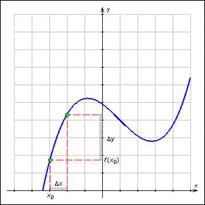
Fie funcția y = f (x) definită pe intervalul X. Luăm un punct. Dați valoarea lui x o creștere. atunci funcția va crește.
Definiția. O funcție derivată y = f (x) este limita raportului dintre creșterea incrementului unei funcții și creșterea incrementului unei variabile independente, deoarece aceasta din urmă tinde la zero (dacă există această limită)
Găsirea derivatului unei funcții se numește diferențierea acestei funcții.
Dacă funcția de la punctul x are un derivat finit, atunci funcția se numește diferențiată în acest punct.
O funcție care poate fi diferențiată în toate punctele din intervalul X se numește diferențiată pe acest interval.
Semnificația geometrică a derivatului. derivatul este panta (panta pantei) a tangentei. trase la curba y = f (x) în punctul respectiv. care este.
Apoi ecuația tangentei la curba y = f (x) în punctul are forma
Semnificația mecanică a derivatului. derivatul timp al căii este viteza momentului în momentul de față:
Sensul economic al derivatului: derivatul volumului producției produse în timp este productivitatea muncii într-un moment.
Relația dintre continuitate și
diferențiabilitatea funcției
Teorema. Dacă funcția y = f (x) este diferențiată la un punct. atunci este continuă în acest moment.
Teorema inversă este falsă, adică dacă funcția este continuă la un anumit punct, atunci nu este neapărat diferențiată în acest moment.
Un exemplu este funcția y = | x |, care este continuă la punctul x = 0, dar are o "pauză" în ea. Derivatul acestei funcții la punctul x = 0 nu există, deoarece.
Astfel, continuitatea unei funcții este o condiție necesară, dar inadecvată pentru diferențiabilitatea unei funcții.
Schema de calculare a instrumentului derivat
Derivatul unei funcții poate fi găsit prin următoarea schemă:
1. Dați argumentul x o creștere și găsiți valoarea incrementată a funcției.
2. Gasiti incrementarea functiei.
3. Formăm relația.
4. Căutăm limita acestei relații. care este (dacă această limită există).
Exemplul 1. Găsiți derivatul unei funcții.
1. Dați argumentul x o creștere și găsiți valoarea incrementată a funcției.
2. Gasiti incrementarea functiei:
3. Formăm relația.
4. Găsiți limita
1. Derivatul constantei este egal cu zero :.
2. Derivatul argumentului este egal cu unul :.
3. Derivatul unei sume este egal cu suma derivatelor acestor funcții
4. Derivatul produsului a două funcții diferențiate este egal cu:
5. Factorul constant poate fi considerat ca un semn al derivatului
6. Derivatul a două funcții parțial diferențiate poate fi găsit din formula:
7. Derivatul unei funcții complexe este
Derivatele funcțiilor elementare de bază: