Decontarea și grafica numărul 2
Partea 2. Intersecția reciprocă a cadavrelor
Pentru a stăpâni metodele de bază ale construirii liniei de intersecție a corpurilor geometrice. Pentru a studia metoda avioanelor auxiliare și metoda sferelor. Aflați cum să le utilizați atunci când rezolvați probleme complexe.
Pentru a efectua lucrarea trebuie să cunoașteți prevederile de bază ale geometriei descriptive:
-conceptul de linie curbă;
-conceptele punctelor de referință;
-esența metodei planurilor auxiliare;
-esența metodei sferelor concentrice și a domeniului de aplicare a acesteia;
- Esența metodei sferelor excentrice și a domeniului de aplicare a acesteia.
Lucrarea constă în două sarcini, a căror soluționare este necesară pentru a putea:
-utilizați aceste metode;
-să poată găsi puncte de referință, puncte de vizibilitate;
-găsiți proiecțiile punctelor care aparțin suprafeței.
Lucrarea se realizează în format A2. Datele inițiale, un cadru, o ștampilă pentru a executa creion simplu în conformitate cu GOST ESKD. Construcții suplimentare pentru realizarea cu creioane colorate sau pastă (albastru, verde etc.), rezultatul final al construcțiilor ar trebui să fie evidențiat cu roșu.
Toate inscripțiile din desen sunt executate cu un simplu font al creionului nr. 5, indici - număr de font 3,5.
Datele inițiale la sarcina 1 sunt prezentate în Anexa A, la sarcina 2 - în Anexa B.
Metoda de planuri auxiliare de tăiere
Metoda este utilizată pentru a determina proiecțiile liniilor de intersecție a două corpuri geometrice: un polyhedron și o suprafață de rotație, două polyhedra, două suprafețe de rotație.
La rezolvarea problemelor de intersecție reciprocă a suprafețelor, trebuie amintite următoarele prevederi:
1. Pentru a găsi punctul de intersecție a liniilor aparținând celor două corpul geometric trebuie să taie planul minor, astfel încât planul secțiunii transversale formate simple, figuri - segment, cerc, triunghi, dreptunghi. Considerăm intersecția de forme simple și definește termenii generali. Utilizarea mai multor planuri de referință pentru a determina numărul de puncte de intersecție a liniei. Conectați numai punctele care sunt pe aceeași față a poliedru.
2. Atunci când suprafața laterală a cilindrului sau a prismei are un relativ plan de proiecție poziție (perpendicular pe această suprafață formând un plan de proiecție) proeminente, apoi o linie de intersecție a proiecției este deja și coincide cu suprafața de proiecție.
3. Dacă linia aparținând suprafeței nu este complet vizibilă, punctele de tranziție de la partea vizibilă a liniei de intersecție la linia invizibilă sunt situate pe schița corpului geometric. Partea vizibilă a liniei de intersecție trebuie să fie vizibilă simultan pentru două corpuri geometrice.
4, este necesar să se ia un avion, care trebuie să treacă prin vârful conului perpendicular pe fețele poliedrului (marginile poliedru), în scopul de a găsi un punct superior sau inferior al liniei de intersecție (un con și un poliedru), fața corespunzătoare a conului.
5. Pentru a găsi punctul de sus sau de jos al liniei de intersecție (sferă și cilindru), este necesar să se deseneze un plan auxiliar prin axele celor două suprafețe.
Starea problemei 1:
Construiți proiecțiile liniei de intersecție a două corpuri geometrice. Când rezolvați o problemă, utilizați metoda de planuri auxiliare secante.
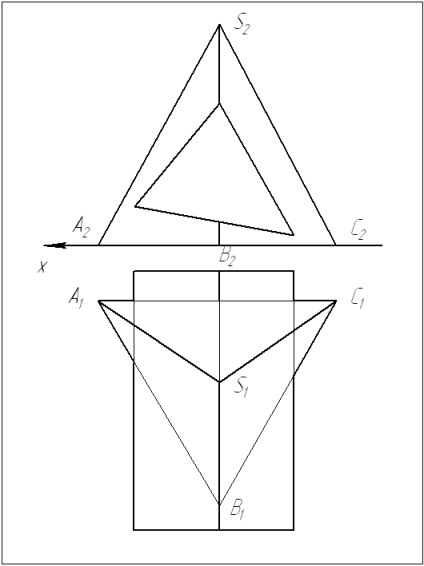
Algoritm pentru rezolvarea problemei:
1 În această problemă, generatoarele (marginile) prismei sunt situate perpendicular pe planul proeminențelor P2. prin urmare, există deja o proiecție finalizată a liniei de intersecție - în planul P2.
Atunci când se rezolvă o problemă, este mai întâi necesar să se găsească punctele de referință - punctele cele mai înalte și cele mai joase sau punctele care pot fi determinate fără construcții suplimentare. Gasim cel mai inalt punct 1.
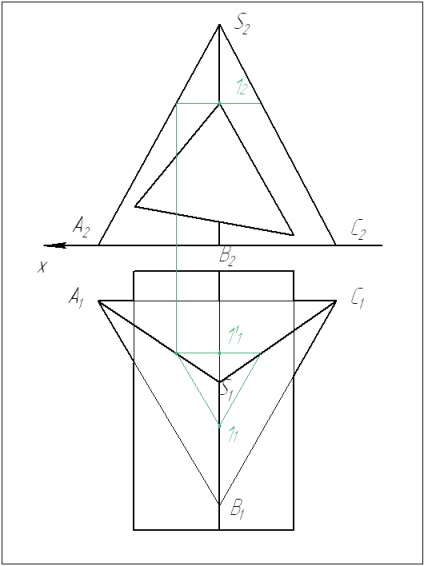
Determinați punctele de referință rămase - 2 și 3.
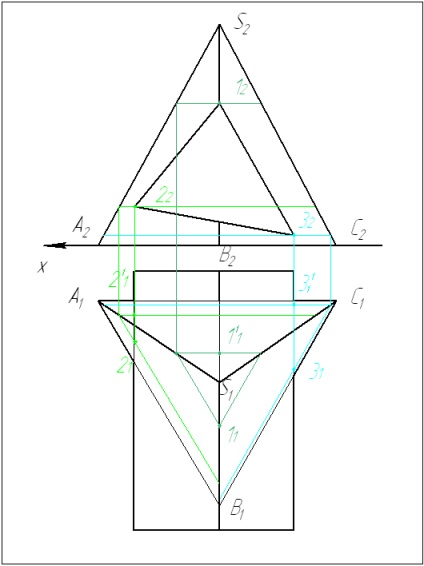
2 Între punctele de referință, tragem un plan auxiliar secant, astfel încât în secțiune se formează forme simple: un triunghi (pentru o piramidă) și un dreptunghi (pentru o prismă). Intersecția acestor cifre ne oferă punctele 4 și 5 dorite.
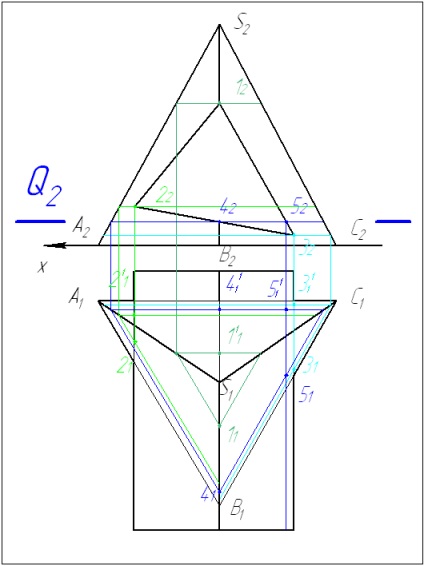
3 Dacă există o linie de intersecție a suprafețelor de rotație, trebuie să fie desenate mai multe planuri auxiliare. Pentru a determina linia de intersecție a suprafețelor feței, este suficient să se găsească punctele de intersecție ale fețelor cu marginile și să se obțină proeminențele liniei de intersecție întreruptă.
4 Conectăm punctele în secvența definită pe planul frontal al proiecțiilor. Determinați vizibilitatea liniei de intersecție rezultată.
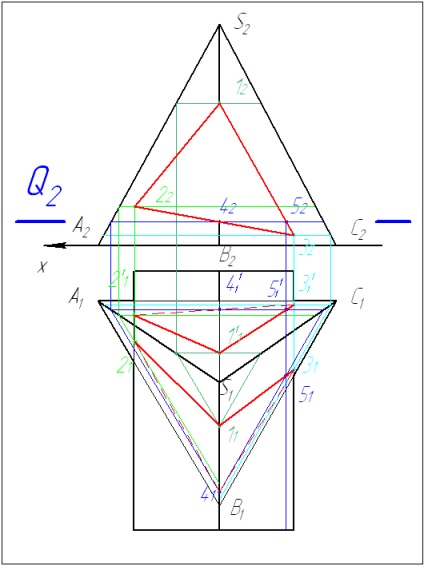
Există două tipuri de metode de sfere:
- metoda sferelor concentrice;
-metoda sferelor excentrice.
Pentru fiecare dintre aceste metode, există un număr de limitări în domeniul de aplicare. Metoda sferică este aplicabilă dacă:
- Ambele corpuri geometrice sunt suprafețe de revoluție;
- Axele suprafețelor se află într-un plan paralel cu planul proeminențelor.
Esența metodei sferelor este următoarea:
La intersecția axelor suprafețelor, centrul sferelor este luat. Se trasează o sferă de rază arbitrară. Sfera intersectează suprafețele de-a lungul cercurilor, care pe diagramă degenerează în segmente. Considerăm intersecția segmentelor, căutăm puncte comune. Punctele găsite vor aparține liniei dorite de intersecție a suprafețelor. Realizăm următoarea sferă auxiliară, repetăm construcția și așa mai departe. Conectăm punctele găsite printr-o curbă netedă.
Luați în considerare intersecția suprafețelor.
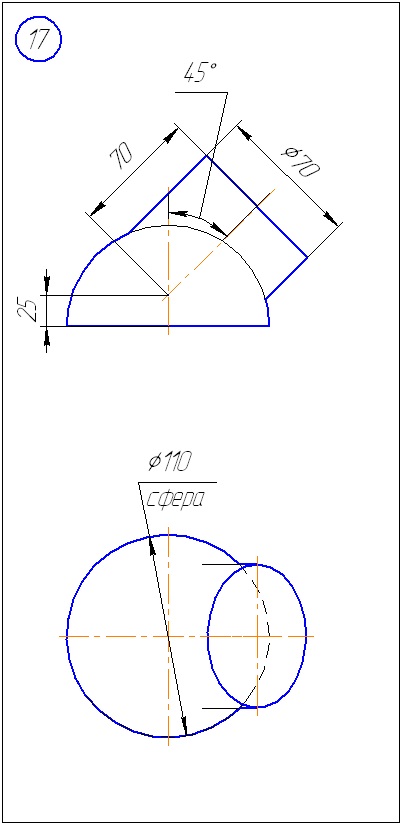
Problema 1. Construiți o linie de intersecție a două suprafețe, dintre care una este o sferă. Determinați vizibilitatea. Problema este rezolvată prin metoda sferelor concentrice.
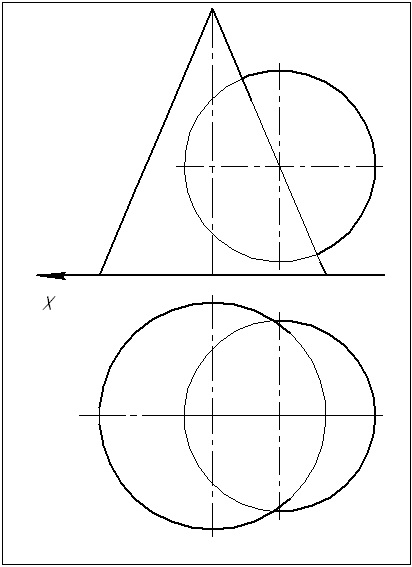
Această problemă poate fi atribuită unui caz particular. În acest fel, puteți rezolva problema numai dacă unul dintre corpuri este o sferă.
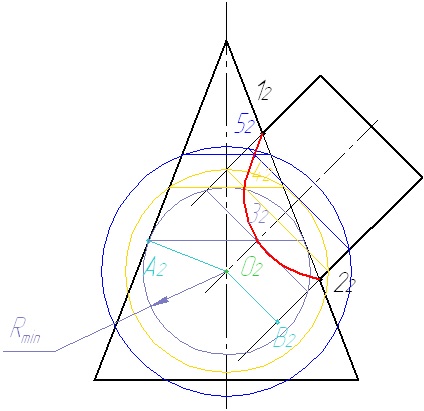
1. Determinați punctele de referință: cea mai mare 1 și cea mai mică 2. Noi găsim proiecțiile lor.
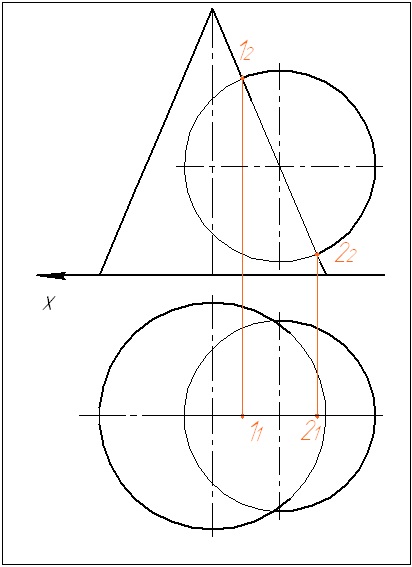
2. Pe axa conului, alegem arbitrar punctul O2, centrul sferelor. Determinăm valoarea razei minime admisibile a sferei:
.
Determinați raza maximă permisă a sferei:
.
Gama de raze de sfere:
.

3. Noi conducem sfera auxiliară. Definim intersecția unei sfere cu suprafețe ca punct de intersecție a caracteristicilor suprafețelor cu un arc. Desenăm segmentele și determinăm punctul lor de intersecție.
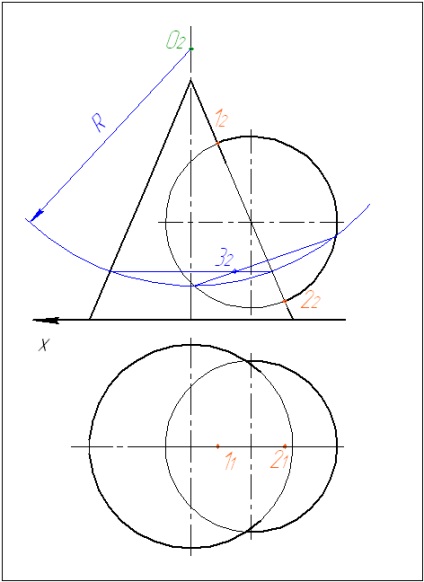
4. Realizați următoarea sferă. Construiți repetarea.
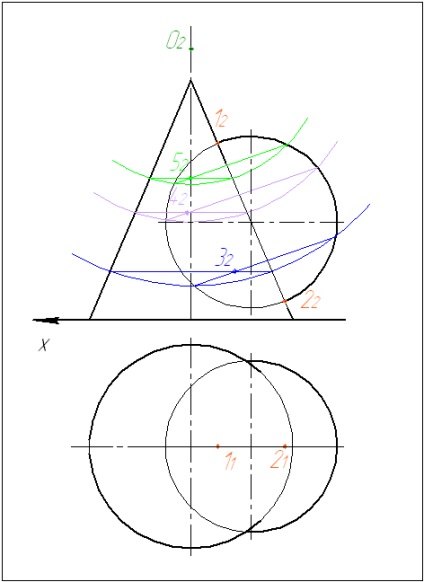
5. Conectați punctele rezultate la o curbă netedă.
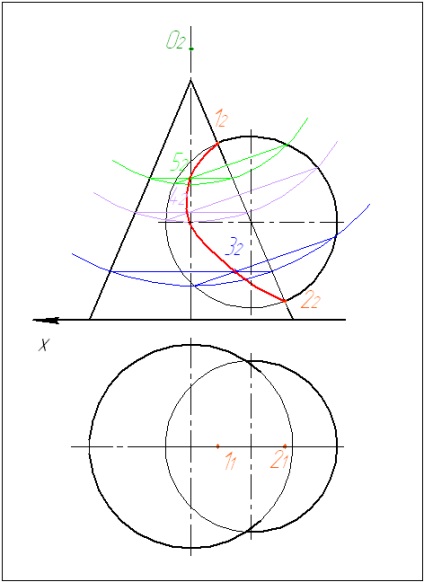
6. Finalizăm proiecția orizontală a liniei de intersecție. Pentru a face acest lucru, considerăm punctele găsite drept puncte care aparțin suprafeței conului. Punctele rezultate sunt conectate printr-o curbă lină luând în considerare vizibilitatea.
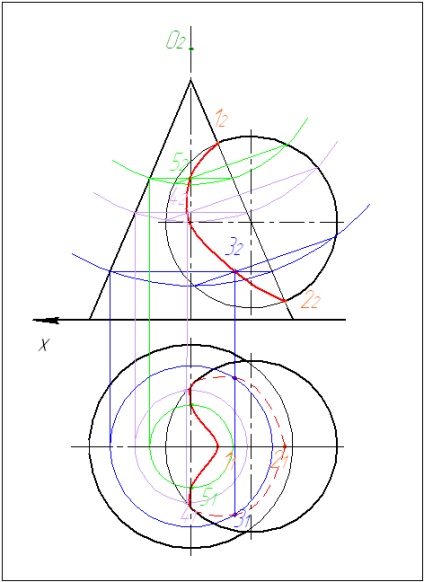
Problema 2. Construiți proiecțiile liniei de intersecție a suprafețelor. Determinați vizibilitatea. Problema este rezolvată prin metoda sferelor concentrice.
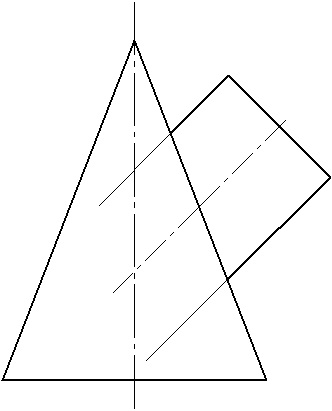
1. Definiți punctele de referință, ca puncte de intersecție a schițelor suprafețelor.
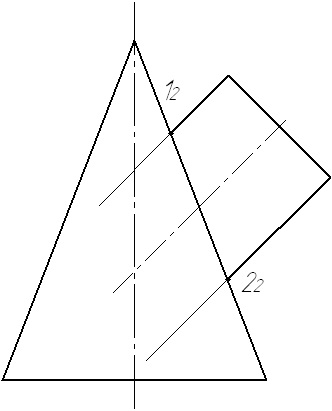
2. Determinați centrul sferelor - ca punct de intersecție a axelor.
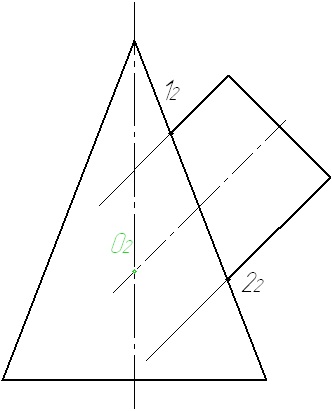
3. Determinați raza maximă posibilă a sferei
4. Stabiliți raza minimă posibilă a sferei. Pentru a face acest lucru, din centrul sferei tragem perpendiculare pe suprafețele generatrice.
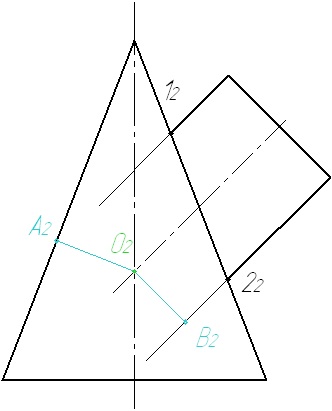
5. Intrăm în sfera razei minime. Sfera atinge suprafața conului de-a lungul circumferinței și traversează suprafața cilindrului de-a lungul circumferinței. Ambele cercuri din diagramă degenerate în segmente. Considerăm intersecția segmentelor, căutăm puncte comune.
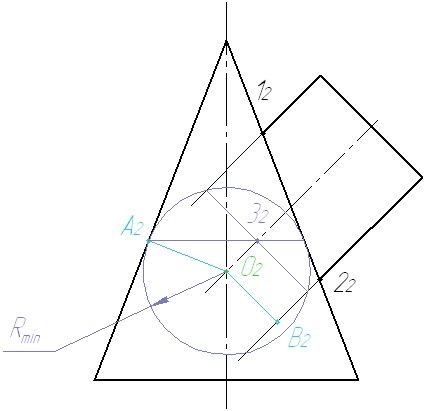
6. Intrăm în sfera de rază arbitrară R. Repetăm construcția.
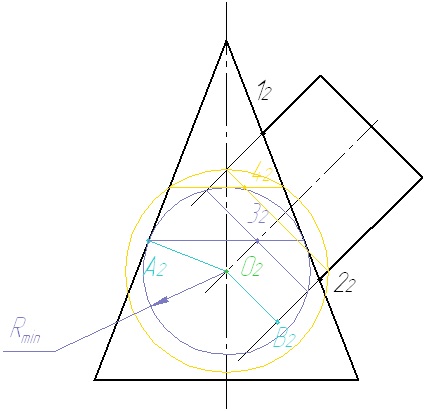
7. Numărul de sfere înscrise trebuie să fie cel puțin trei. Punctele astfel obținute sunt legate printr-o curbă netedă.
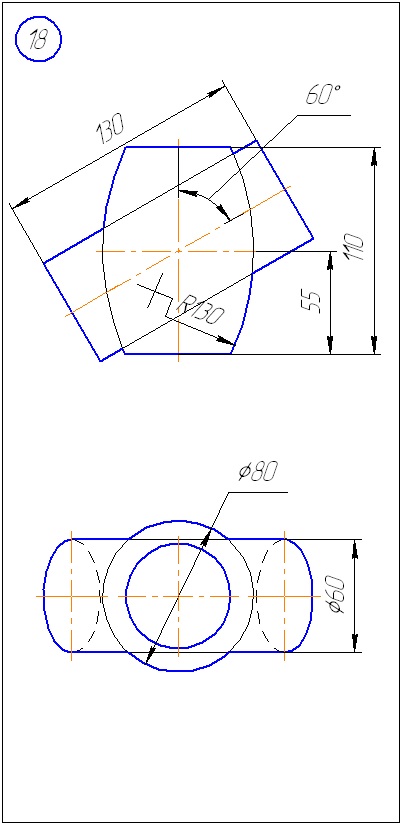
Problema 3. Construiți proiecțiile liniei de intersecție a torusului cu cilindrul. Determinați vizibilitatea. Problema este rezolvată prin metoda sferelor excentrice.
Metoda sferelor excentrice este aplicabilă dacă:
- ambele corpuri geometrice ale suprafeței de revoluție;
- axele suprafețelor se află într-un plan paralel cu planul proeminențelor;
- una dintre suprafețe este un torus.
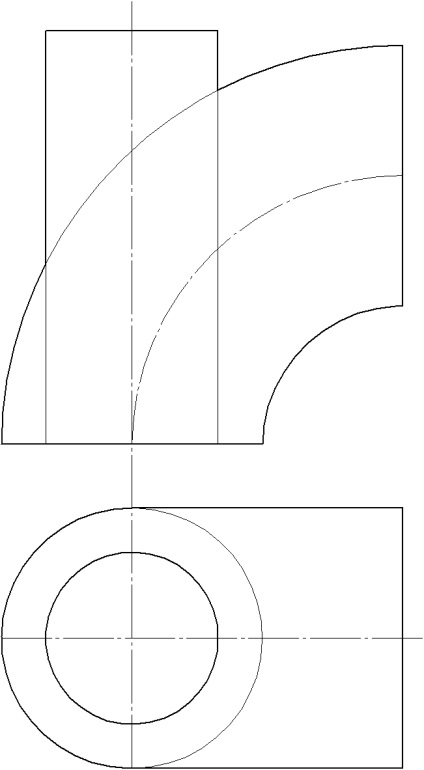
1. Definiți punctele de referință ca puncte de intersecție a eseurilor.
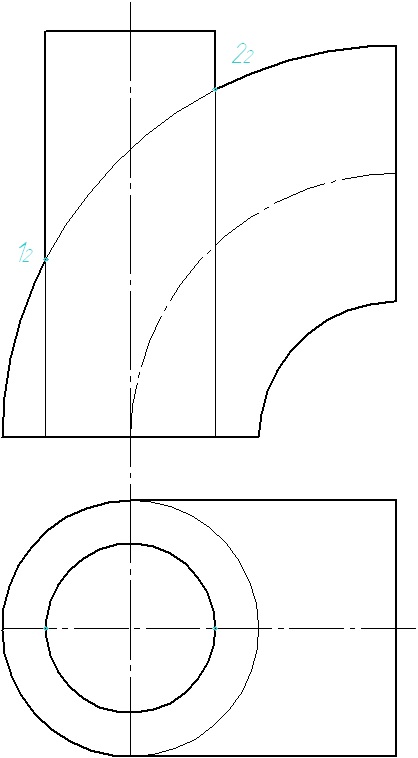
2. Desenăm planul de proiectare în intervalul dintre punctele de referință. Din punctul de intersecție a planului proiectat cu axa torusului, reconstruim perpendicularul pe intersecția cu axa cilindrului. Obținem punctul O - centrul sferelor.
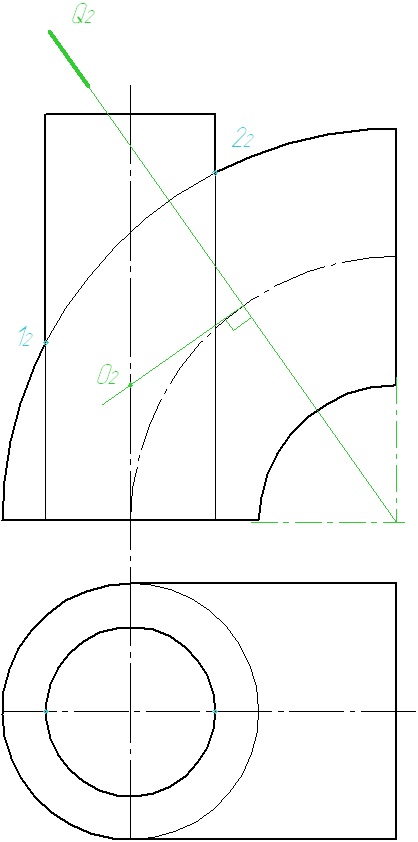
3 Din centrul O2 tragem o sferă de rază R. Sfera va intersecta suprafețele cilindrului și torului de-a lungul cercurilor, care pe diagramă degenerează în segmente. Punctul cerut se află la intersecția segmentelor obținute.
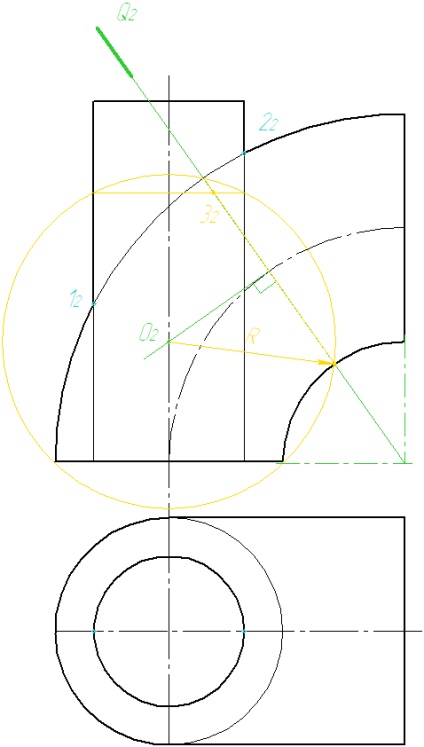
4. Desenați următorul plan de proiecție. Construiți repetarea.
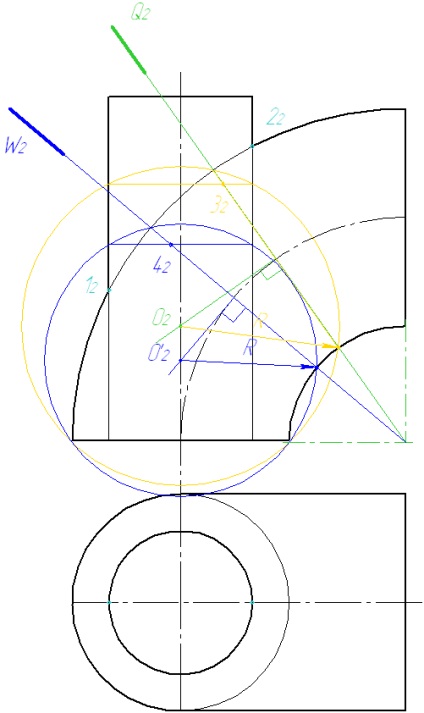
5 Numărul de sfere este ales independent, dar nu mai puțin de trei.
Conectăm punctele obținute cu o curbă netedă. Vom găsi a doua proiecție a liniei de intersecție.
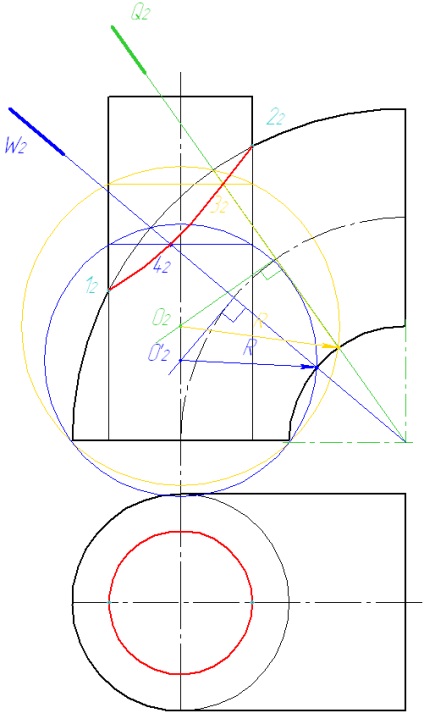
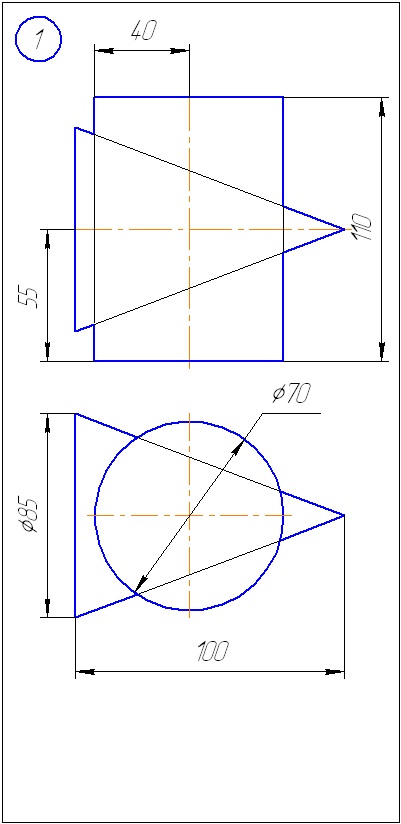
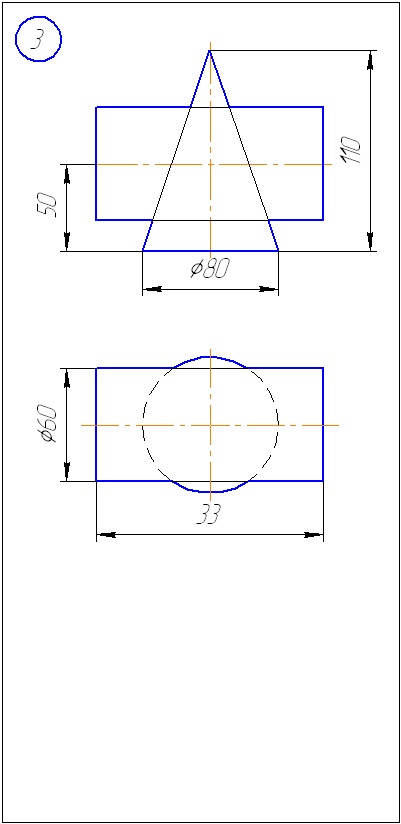
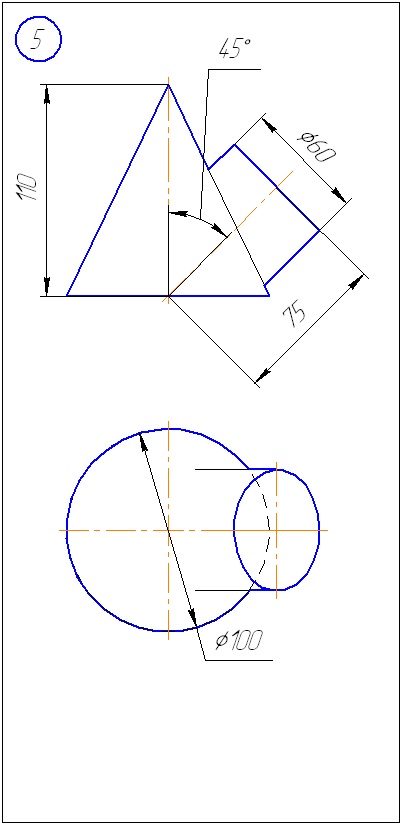
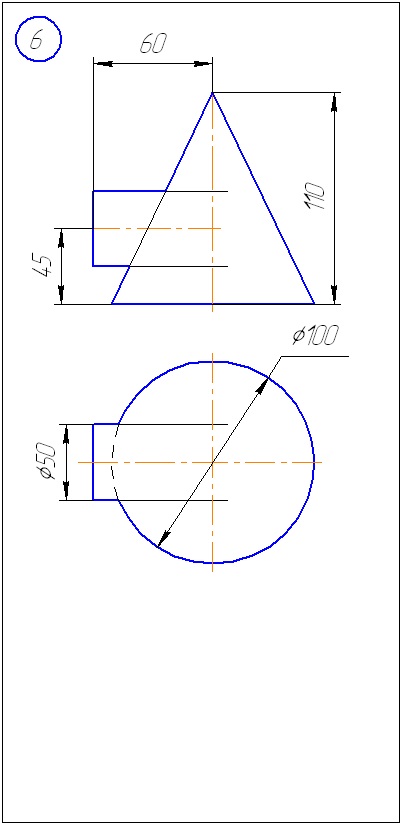
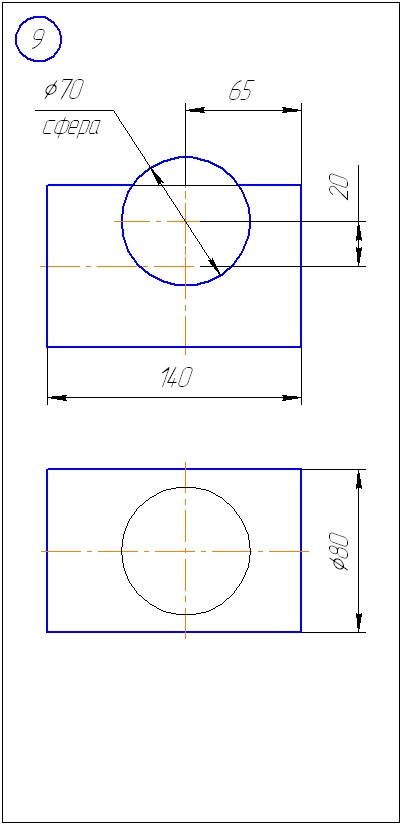
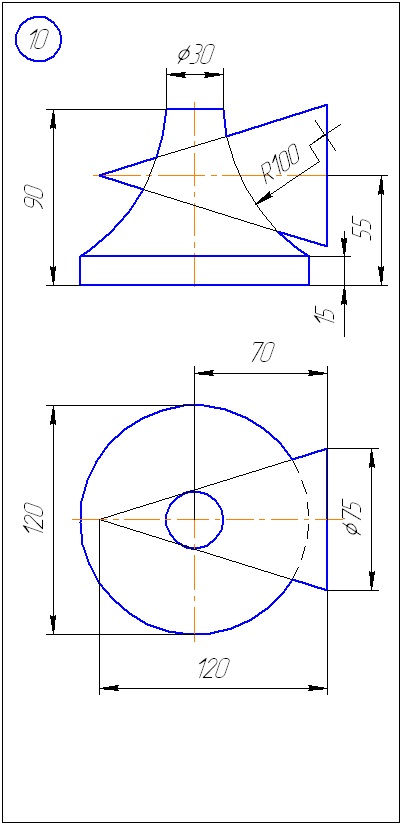
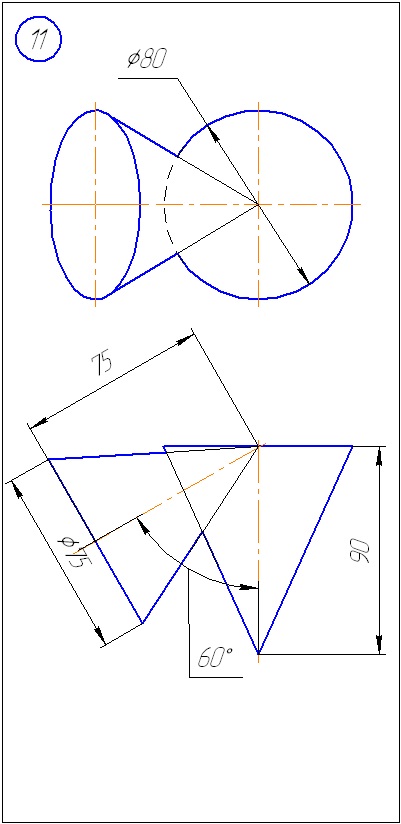
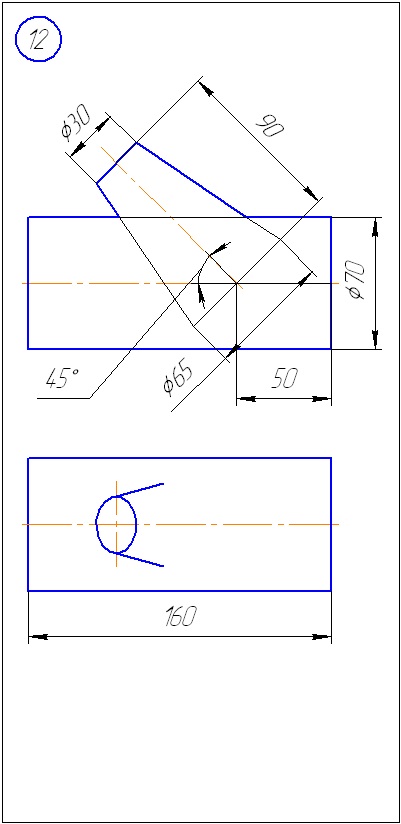
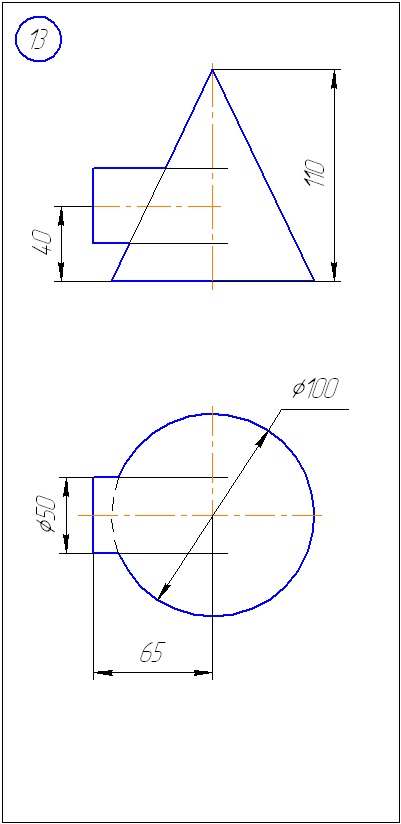
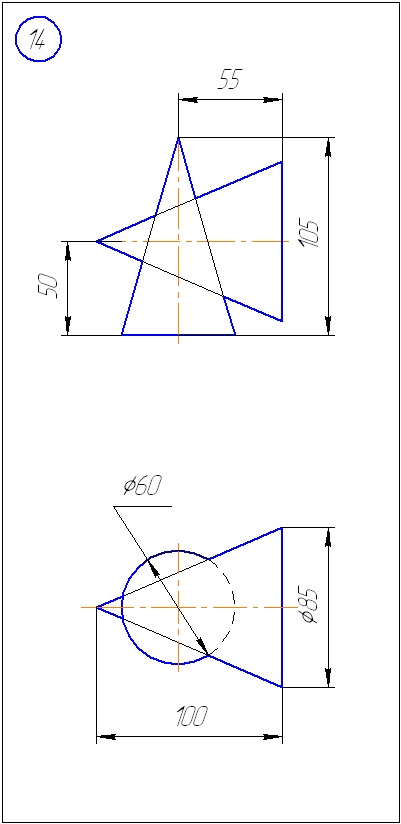
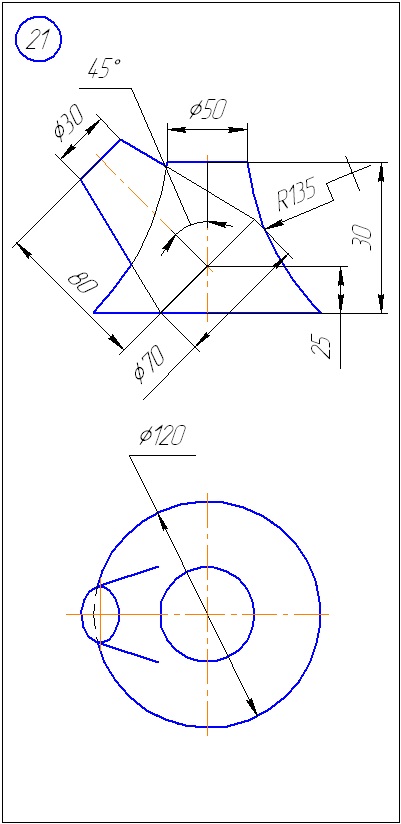
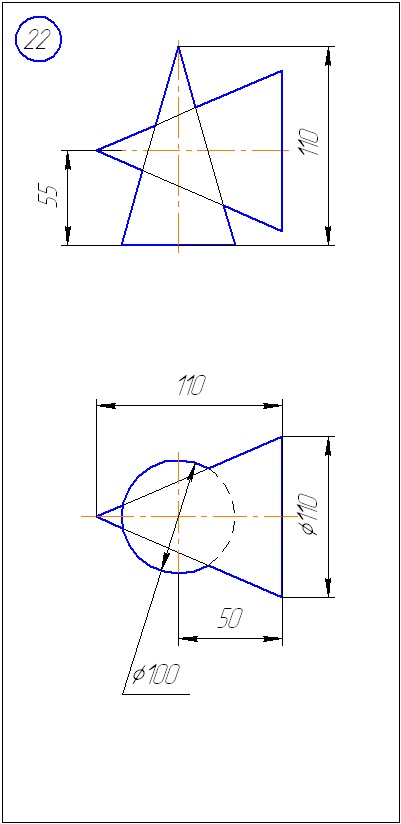
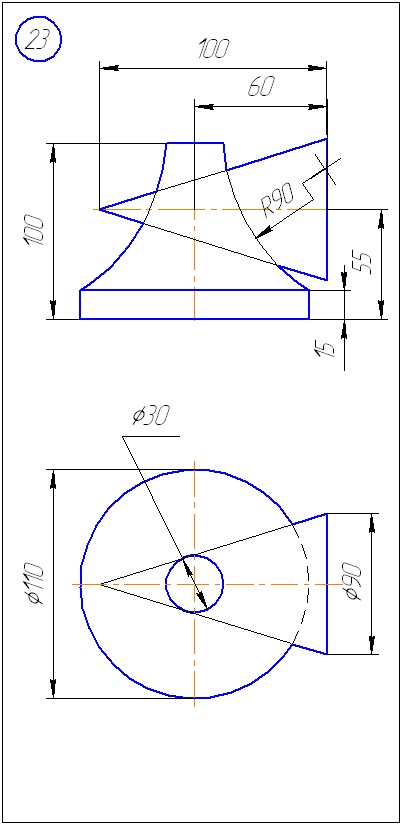
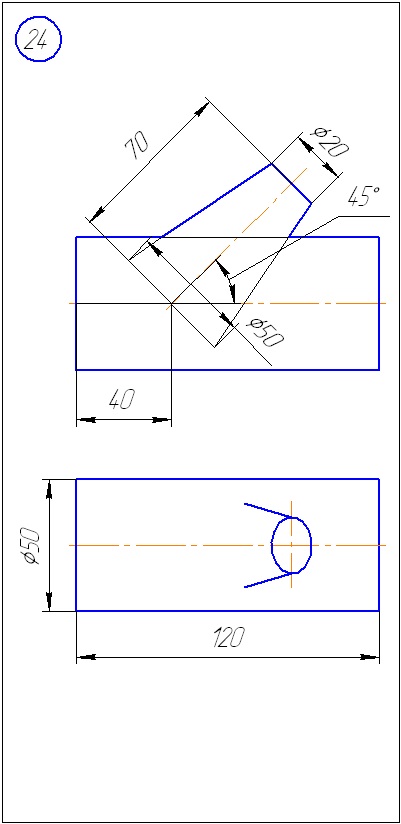
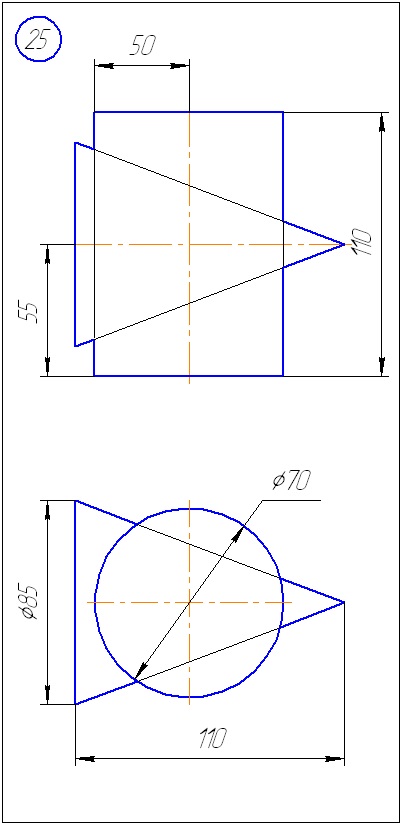
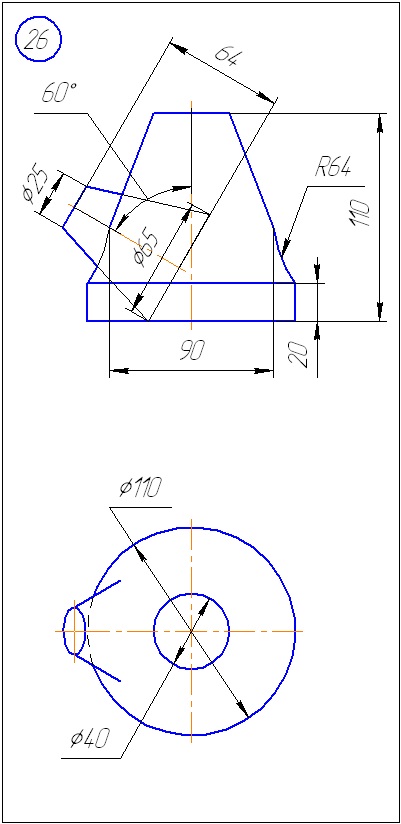
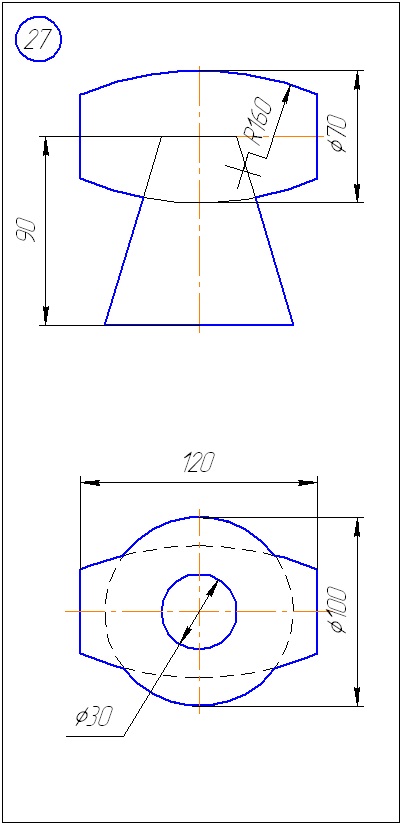
Anexa A - Variante de sarcini pentru sarcina 1 (metoda de tăiere a planelor)
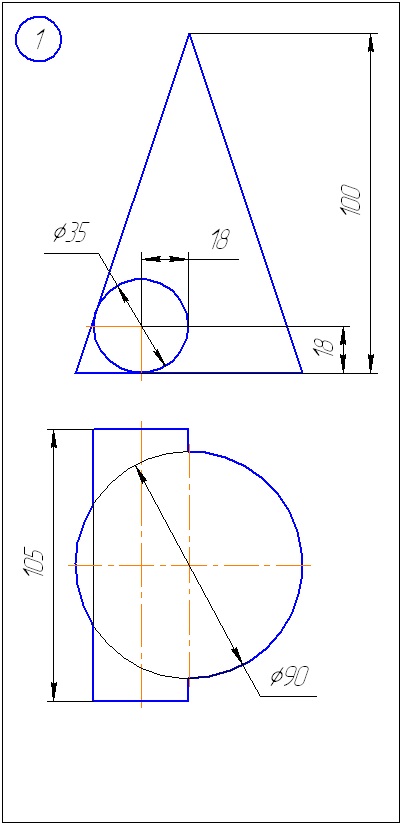
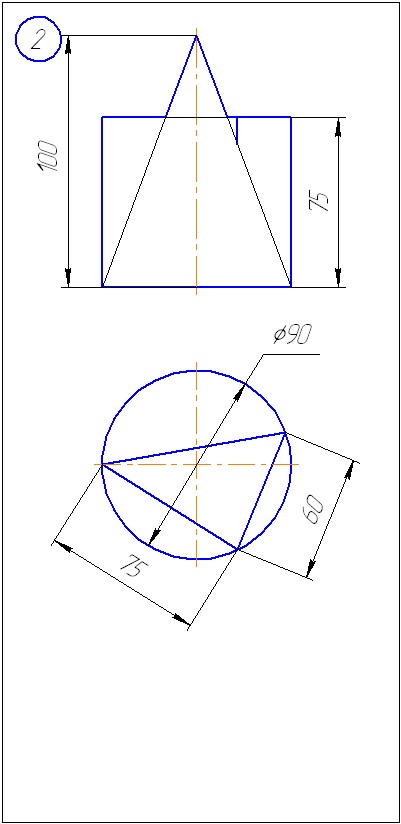
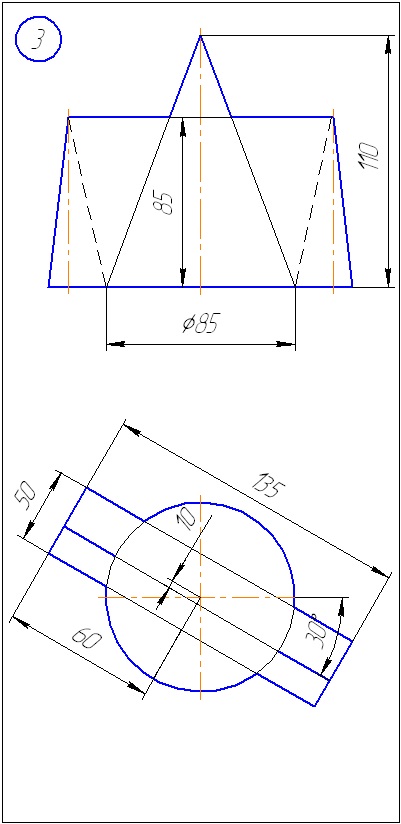
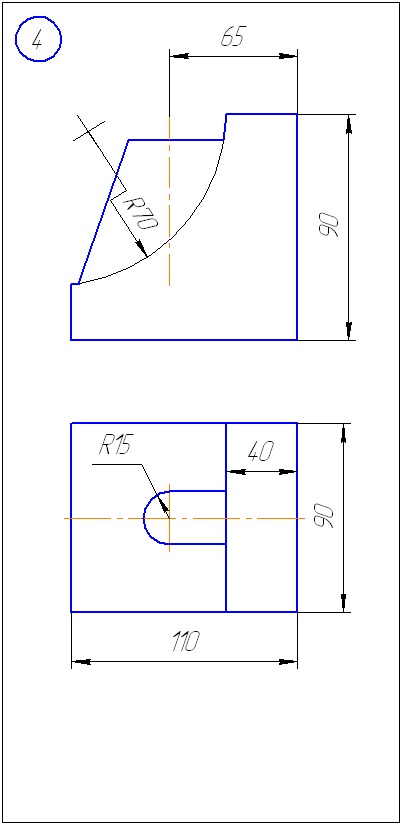
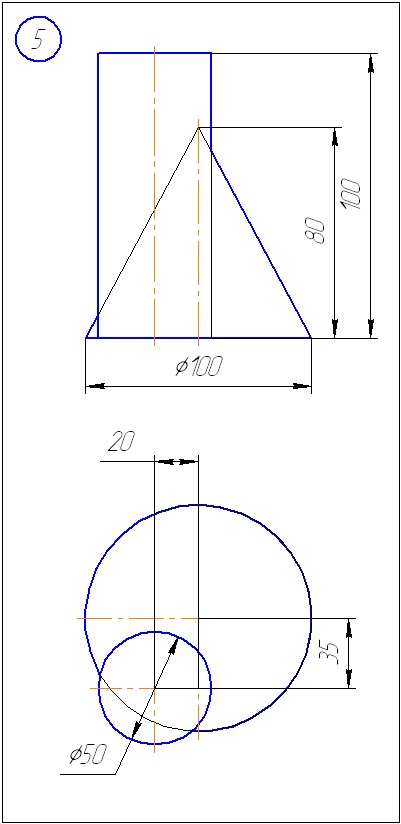
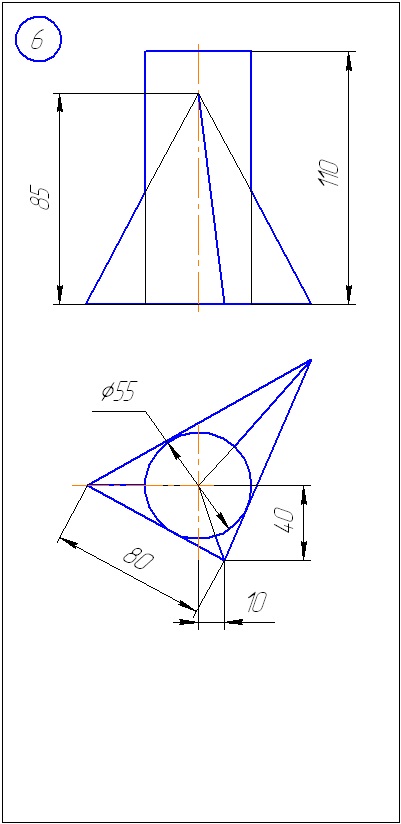
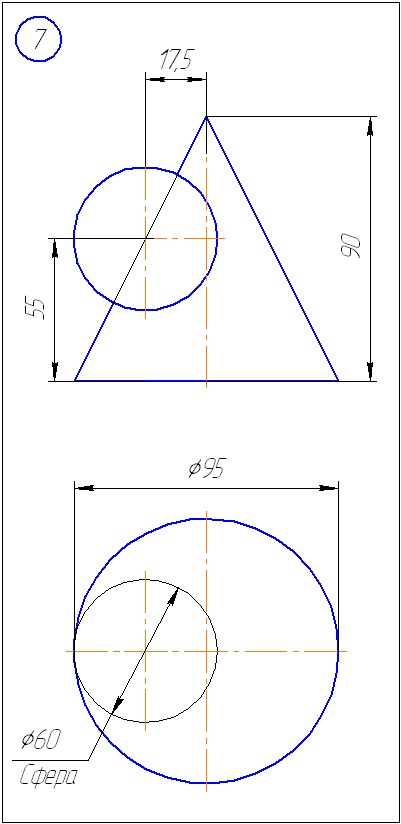
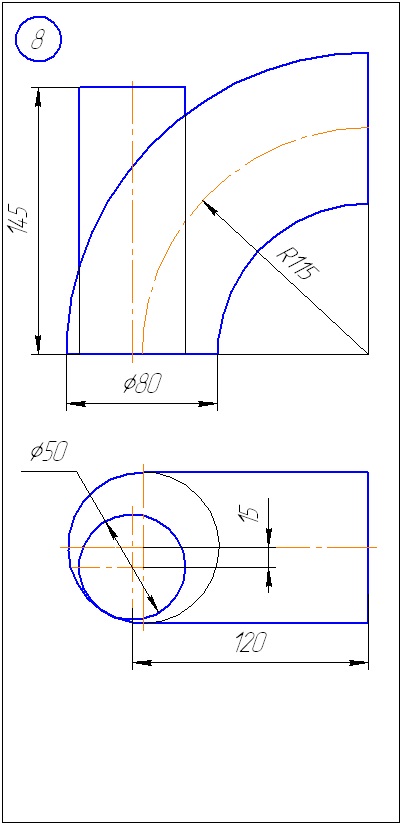
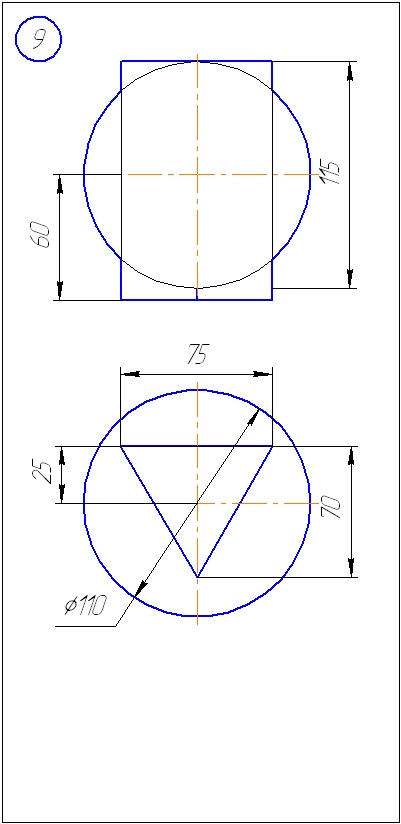
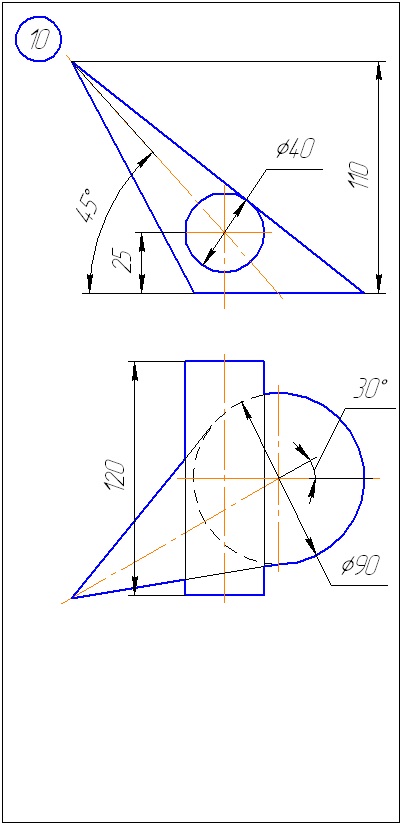
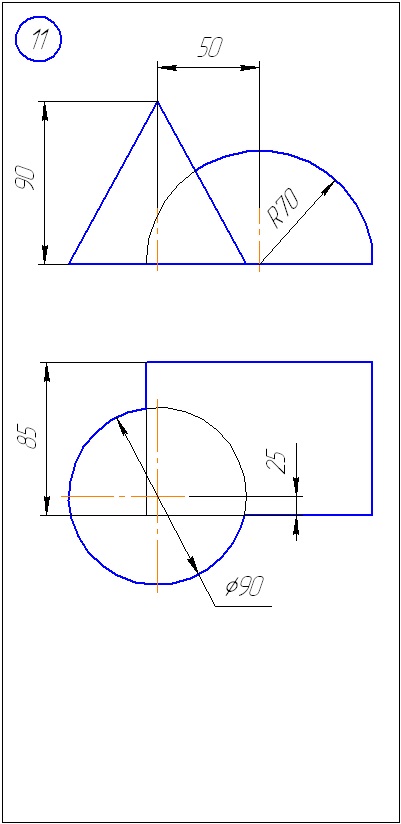
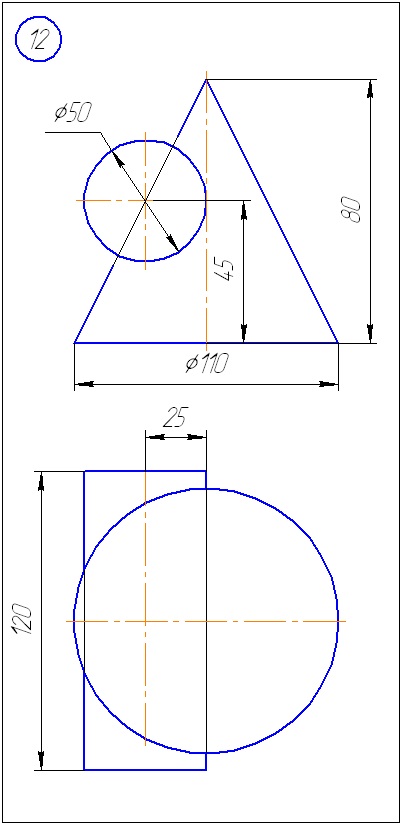
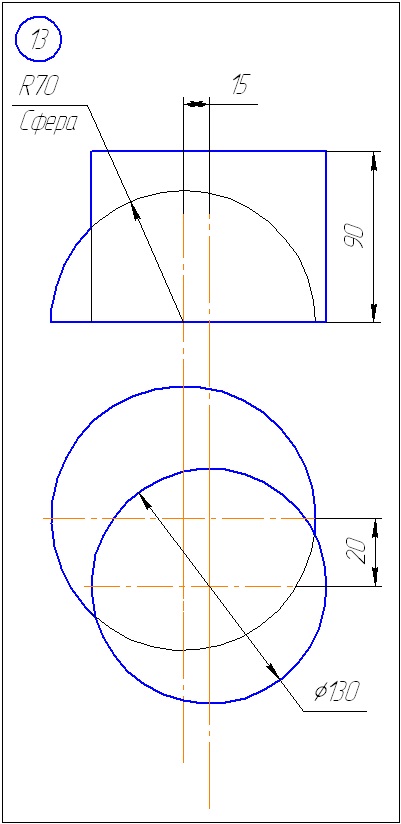
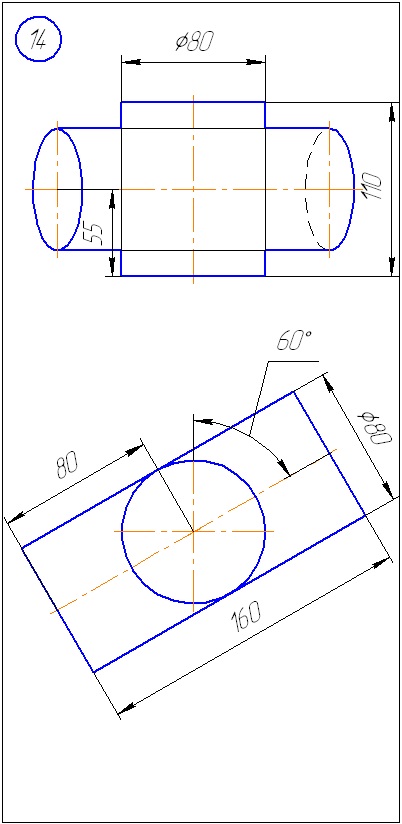
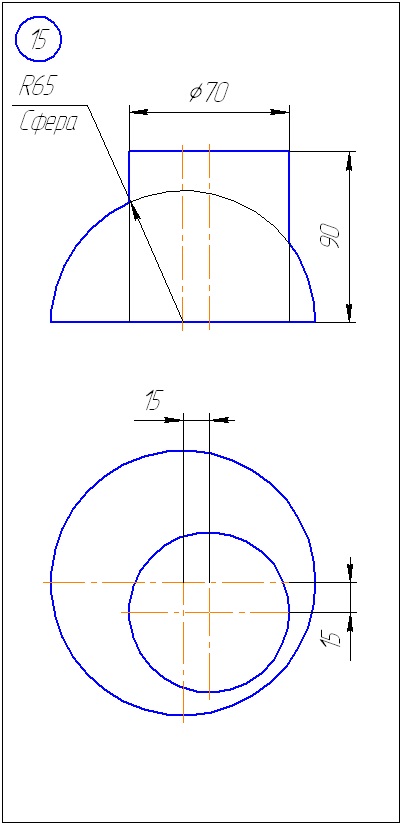
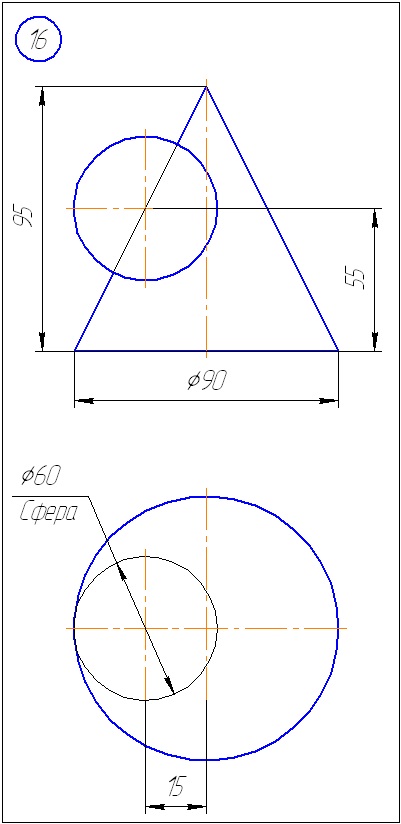
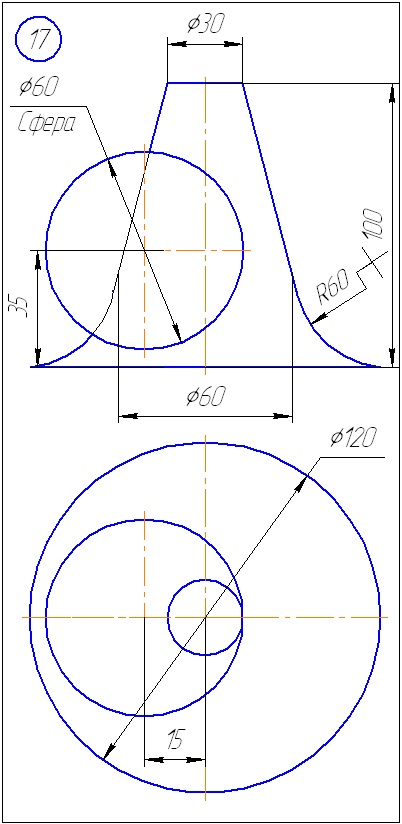
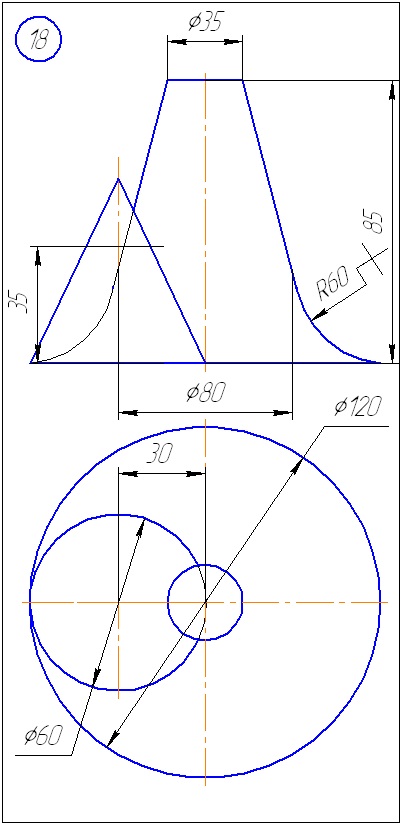
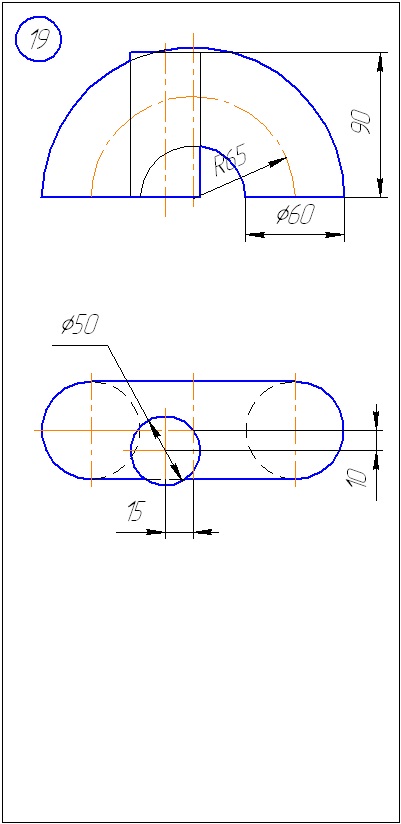
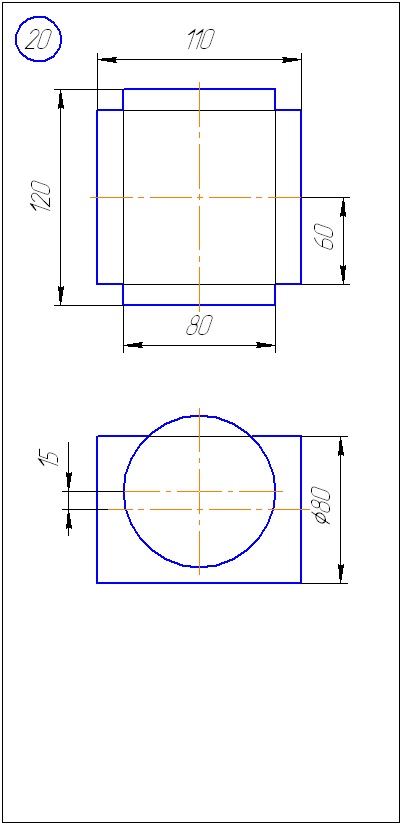
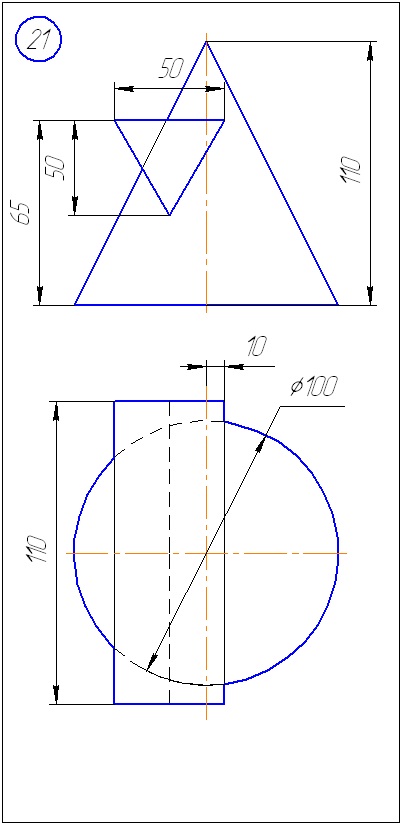
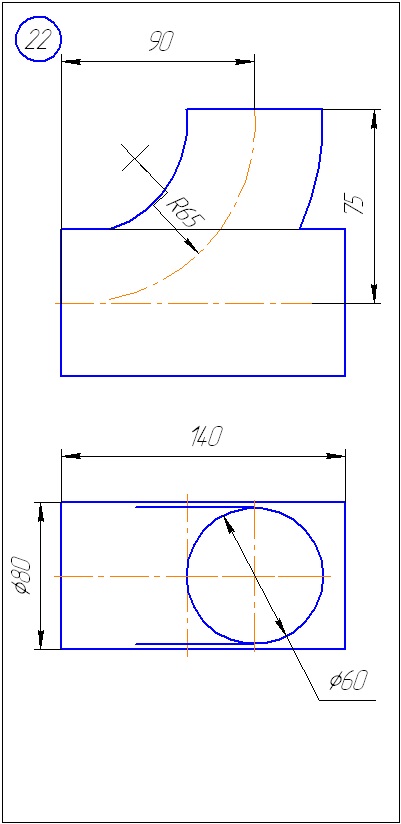
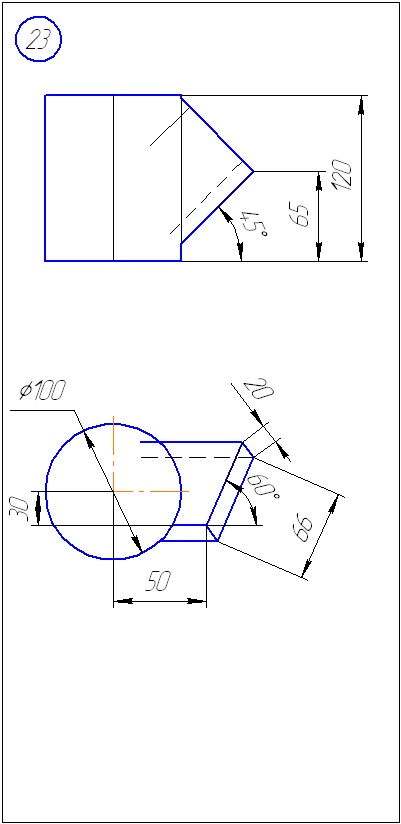
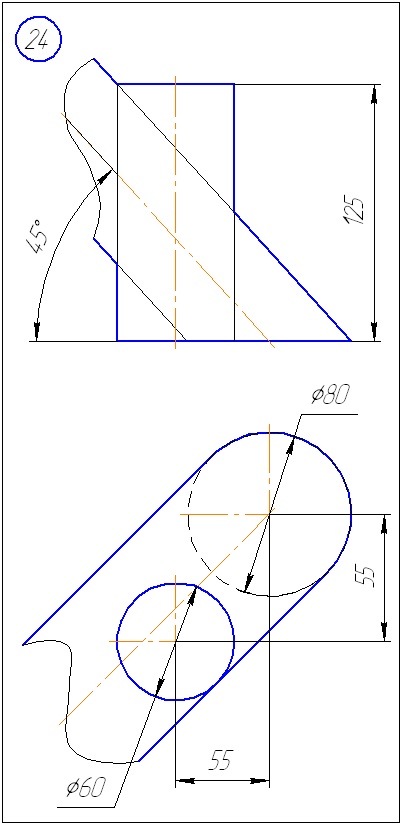
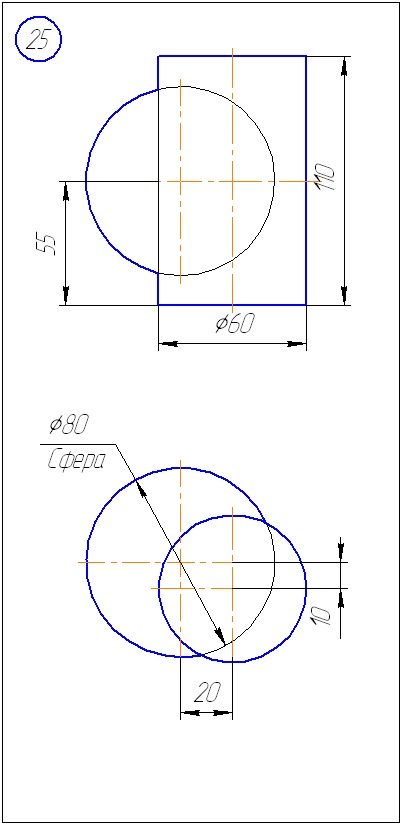
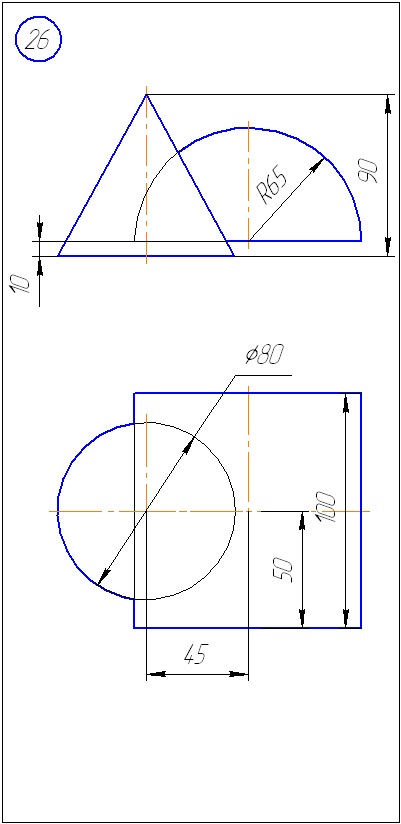
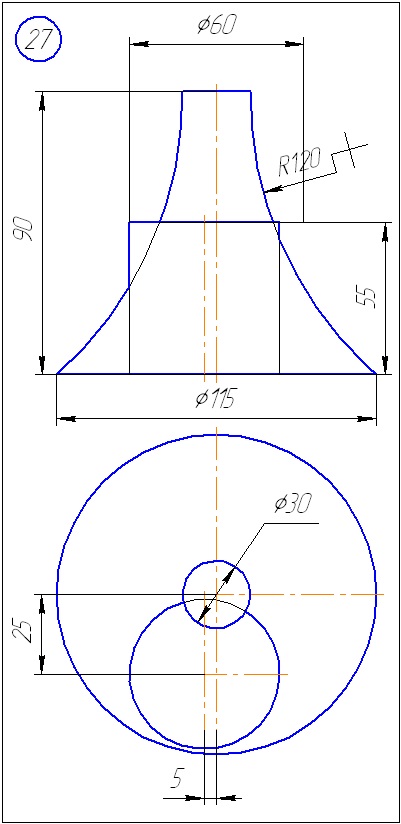
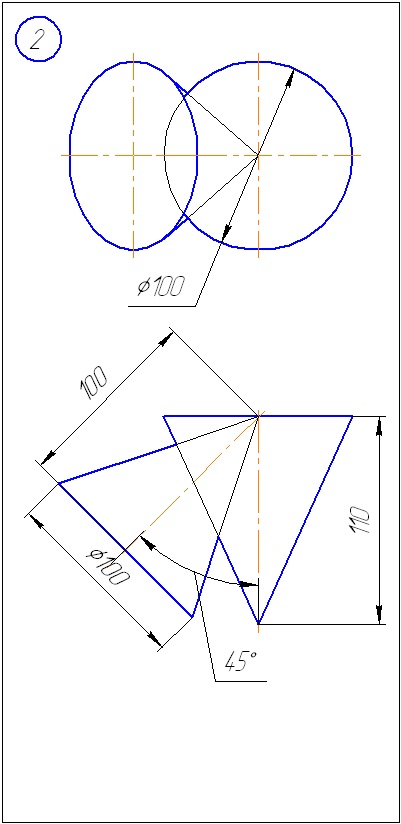
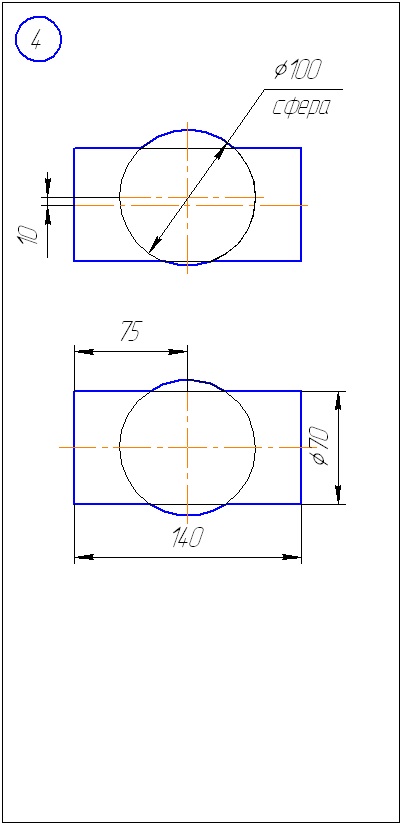
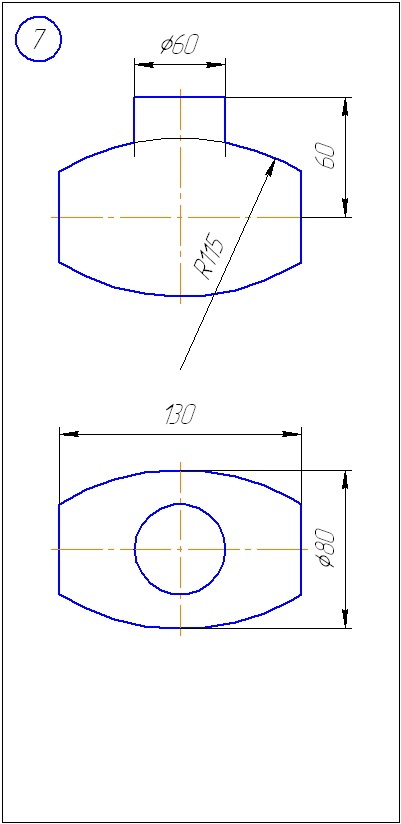
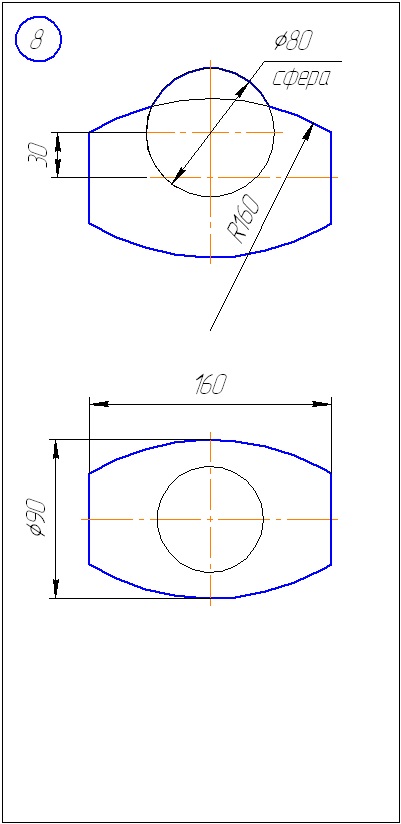
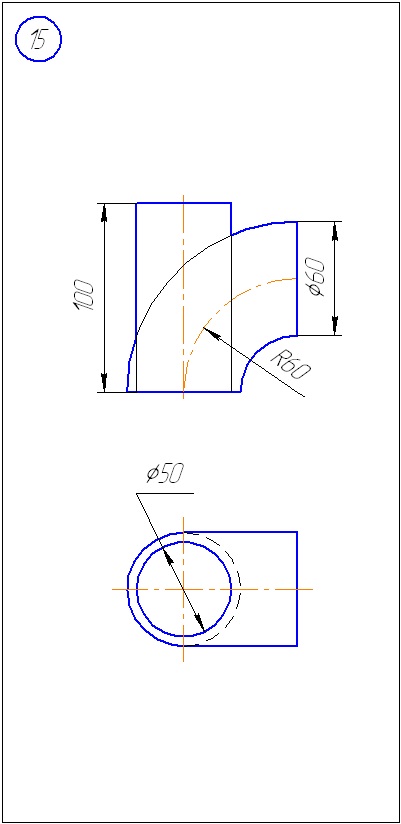
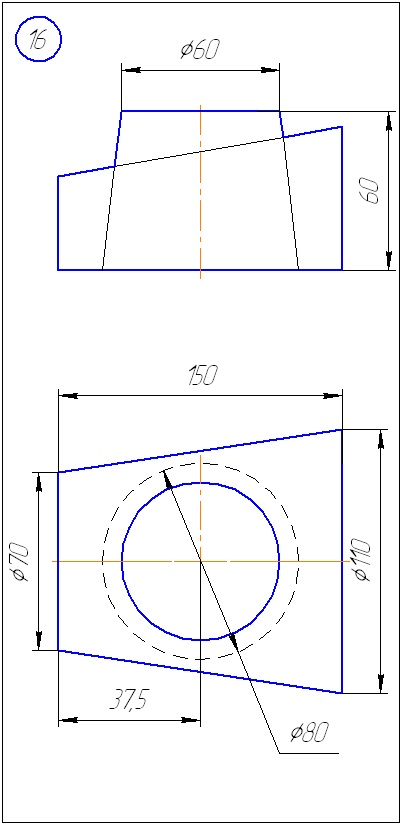
Anexa B - Variante de sarcini la sarcina 2 (metoda sferă)