II. Intersecția suprafețelor curbe
Informații generale despre suprafețe
Modul general de construire a liniei de intersecție a unei suprafețe cu alta
Unele cazuri speciale de intersecție a unei suprafețe cu alta
Lista literaturii utilizate
Știm că figura intersecției a două linii drepte este un punct și de asemenea știm că figura intersecției a două planuri este o linie dreaptă. Și suprafețele curbate se intersectează. Și astfel obiectivul lucrării noastre este de a afla forma intersecției suprafețelor curbe.
Acest subiect este relevant, deoarece există întotdeauna un interes în construirea de sarcini. În cursul școlii de geometrie, suprafețele curbe și cazurile de intersecție nu sunt luate în considerare.
Subiectul studiului nostru este intersecția suprafețelor curbe, iar obiectul investigației noastre este suprafața curbată.
Următoarele metode sunt utilizate în lucrare:
· Lucrul cu literatura științifică
· Lucrul cu literatura de specialitate
Informații generale despre suprafețe
Suprafața este locul geometric al unei linii care se deplasează în spațiu conform unei anumite legi. Această linie este numită generatrix. Poate fi dreaptă, atunci suprafața formată la ea se referă la clasa celor condamnați. Dacă generatorul este o linie curbă, suprafața este considerată neliniară. Linia de-a lungul căreia se deplasează generatorul se numește ghidaj. Ca și cea din urmă, uneori se utilizează o urmă a suprafeței.
Determinantul unei suprafețe este setul de condiții care definesc o suprafață în spațiu.
Suprafața este considerată dată dacă este posibilă construirea proiecțiilor oricărui generator. Una și aceeași suprafață poate fi formată prin mișcarea diferitelor linii. De exemplu, sfera este formată prin rotirea unui cerc în jurul diametrului său.
Suprafețele considerate mai jos sunt clasificate după cum urmează.
I. Sunt influențate suprafețele de rotație.
3. Hiperboloidul cu o singură cavitate.
II. Suprafețele de rotație sunt neliniar.
2. Tor (circular, parabolic, eliptic).
3. Elipsoid (alungit și comprimat).
4. Suprafața de revoluție a formei generale.
Sunt conduse suprafețele de rotație.
Toate suprafețele din această clasă sunt formate prin rotirea unei linii drepte în jurul unei alte linii drepte. Două linii drepte pot ocupa trei poziții diferite unul față de celălalt. Fiecare dintre ele are propria suprafață de revoluție.
1. Conul este format prin rotirea liniei drepte OD în jurul axei Z ce se intersectează cu ea (figura 2, a). Planurile de coordonate XOZ și YOZ disecă conul de-a lungul liniilor drepte intersectate OD, OE, OK și OF; planul XOZ dă punctul O în secțiune; avionul. paralel cu XOY, intersectează circumferința (DFEK).
Pentru a construi un punct aparținând curbei suprafeței, suprafața sa este situată pe proeminențele liniei situate pe această suprafață.
Cone participă la formarea formei antenei de model radiație, poziția suprafeței obiectului în spațiu, antena și hrana acestuia, conul difuzorului, reflectorul cavitate undelor radio, tuburi electronice și tuburi cu vid, fibre, piese de echipamente de vacuum și așa mai departe.
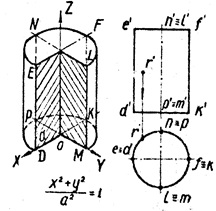
2. Cilindrul este format prin rotirea liniei drepte ED în jurul axei Z paralele cu ea (Figura 2, b, c)
XOZi plan YOZ trec prin linii paralele ED, FK, NP, LM, și planul XOY și paralele cu ea - de-a lungul cercurilor DPKM și (ENFL).
Cilindrul este utilizat pentru a forma ghiduri de undă, antene, amortizoare de amortizare pentru instrumente, oglinzi laser, carcase de senzori și așa mai departe.
Suprafețele de rotație sunt neliniar.
La această clasă se află în principal suprafețele formate prin rotirea curbelor de ordinul doi.
1. Sfera este formată prin rotirea cercului în jurul diametrului său (Figura 4). Orice avion intersectează sfera într-un cerc. O schiță a proieciei frontale a sferei se numește meridianul principal, conturul proiecției orizontale este ecuatorul. Proeminențele punctului K care se află pe suprafața sferei aparțin proiecțiilor cercului orizontal desfășurate pe sferă.
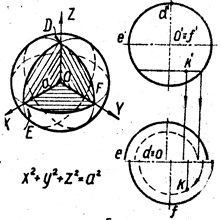
Sfera formează forma antenei, radiomodul și radiatorul antenei, capul microfonului, contactele releului și așa mai departe. Sfera este suprafața poziției obiectului în spațiu.
2. Un torus circular este format prin rotirea unui cerc în jurul unei axe situate în planul acestui cerc și care nu este diametrul său. Astfel, sfera poate fi privită ca un caz special al torusului. Distingeți un inel torus, atunci când axa de rotație nu intersectează cercul de generare și toroanele.
În domeniul radiotehnicii, se utilizează și un torus parabolic și eliptic.
Un torus parabolic se formează prin rotirea unei parabole în jurul unei linii situată în planul acestei parabole și nefiind axa sa focală.
Un torus eliptic este format prin rotirea elipsei pe o linie dreaptă situată în planul acestei elipse și nefiind axa sa.
Suprafețele torsionale au modele de directivitate a antenei, suprafețe de poziționare a obiectelor în spațiu, antene și jgheaburi, ghiduri de undă, rezonatoare, difuzoare și așa mai departe.
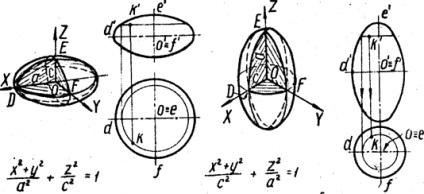
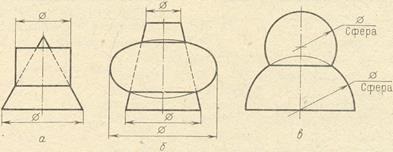
3. Un elipsoid este format prin rotirea unei elipse în jurul axei sale mici sau majore. În primul caz, se obține un comprimat (Figura 5, a), iar în al doilea caz se obțin elipsoidele alungite de rotație (fig.5, b).
Avioanele XOZ și YOZ le traversează de-a lungul elipsei DE și EF, iar planul XOY de-a lungul circumferinței DF.
Forma elipsoidului are oglinzi de antene și lasere, emițătoare de antenă, suprafețe de poziționare și așa mai departe.
4. Suprafața de revoluție a formei generale se formează prin rotația unei curbe arbitrare.
METODA GENERALĂ DE CONSTRUIREA LINIEI DE CONSTRUIREA ALTĂ SUPRAFAȚĂ ALTELE
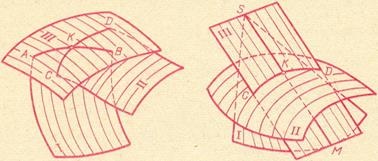
O metodă comună de construire a liniei de intersecție a unei suprafețe a celuilalt este de a găsi puncte de pe această linie, prin intermediul unor suprafețe de trunchiată (pentru linii de trecere, de asemenea, se aplică numit „linie de tranziție“, în special în cazurile în care trecerea de la o suprafață la alta nu este în mod clar de joncțiune definită. Pentru filiala intersectează suprafețele există un nume "intermediari"). Figura 1 din stânga arată că suprafețele I și II sunt intersectate de unele suprafețe III; această suprafață auxiliară intersectează suprafața I de-a lungul liniei AB, iar suprafața II - de-a lungul liniei CD. Punctul K la care intersectează liniile AB și CD, comun pentru suprafețele I și II, aparține liniei intersecției lor. Repetând această metodă, obținem un număr de puncte din linia dorită.
Aplicând această metodă generală pentru construirea liniei de intersecție a două suprafețe curbe, putem:
1) pentru a traversa suprafețele cu planuri auxiliare;
2) intersectează suprafețele prin suprafețe curbe auxiliare (de exemplu, sfere).
În unele cazuri, atunci când se rezolvă problemele, se combină folosirea planelor auxiliare și a suprafețelor curbe. Pe cât posibil, este necesar să se aleagă astfel de suprafețe auxiliare care, atunci când se intersectează cu suprafețele date, dau linii simple (de exemplu linii drepte sau cercuri).
În general, planurile auxiliare secante sunt de asemenea folosite pentru a construi linia de intersecție a curbei suprafeței unei fețe.
Metoda generală descrisă pentru construirea unei linii de intersecție a unei suprafețe a celuilalt nu exclude utilizarea altor mijloace, în cazul în care cel puțin una dintre aceste suprafețe cutate: găsi punctul în care generatoarea dreaptă a unei suprafețe se intersectează cu o altă suprafață, iar prin repetarea acestei tehnici la un număr de generatoare, prin aceste puncte dețin linia dorită. În figura 1 din dreapta, se arată că prin intermediul generatorului SM al suprafeței I este desenat un plan III care intersectează a doua suprafață (II) de-a lungul CD-ului curbei; generatorul SM intersectează această curbă la punctul K, prin care trece linia de intersecție necesară a suprafețelor I și II.
Acest lucru se aplică și în cazul intersecției curbei suprafeței unei fețe: aici rolul generatoarelor este jucat de marginile feței.
Deci, pentru a construi linia de puncte, rezultând într-o suprafață la intersecția altor suprafața sa, sunt planuri care se intersectează auxiliare private și poziția generală, suprafețe curbe, generatoare rectilinii curbele de suprafețe cutate și marginile suprafețe fatetate. Procedând astfel, ei recurg la modalități de a transforma desenul, dacă aceasta simplifică și perfecționează construcția.
Atunci când se construiesc puncte ale liniei de intersecție, este mai întâi necesar să găsim acele puncte, care de obicei sunt numite caracteristice (pentru care se folosește și numele "suport"). Acest punct a cărui proiecții separate partea vizibilă a liniei de intersecție a proiecției invizibilului, proiecțiile punctelor de linii de intersecție ale cea mai joasă și cea mai mare în raport cu π1 avionul, cel mai apropiat și cel mai îndepărtat în raport cu privitorul, extrema stângă și dreaptă a liniei de intersecție a proiecțiilor.
Unele cazuri speciale de traversare a unei alte suprafețe altfel
1. Figura 2 prezintă intersectarea: a) doi cilindri cu generatori paraleli, b) doi conuri cu un vârf comun. În ambele cazuri, liniile de intersecție a suprafețelor sunt generatoare generice ale acestor suprafețe.
Să presupunem că trebuie să construim proiecțiile unei linii drepte care trece prin punctul B pe axa proeminențelor și situată sub un unghi 1 față de planul π1 și sub un unghi 2 la planul π 2. Se știe că pentru o poziție generală directă # 966; 1 + # 966; 2<90градусов.
Locul geometric al liniilor care trec printr-un anumit punct și fac un unghi cu planul π1 1, este o suprafață conică a revoluției a cărei vârf este la un punct dat, iar generatoarele compun un unghi cu planul π1 # 1;
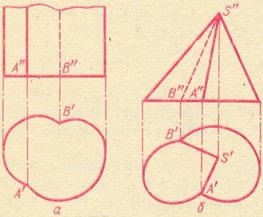
În mod similar, locusul liniilor care trec printr-un punct dat și făcând un unghi cu planul π2 2, este o suprafață conică a revoluției a cărei vârf este la un punct dat, iar generatoarele compun un unghi cu planul π2 # 966;
Evident, linia dorită trebuie să aparțină simultan suprafețelor ambelor conuri care au un vârf comun la un punct dat, adică, Ar trebui să fie o linie a intersecției lor - generația lor comună. Obținem opt raze care ies din punctul B, care corespund condițiilor date (patru linii).
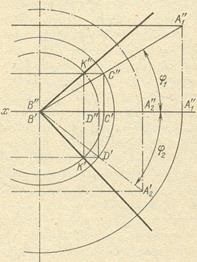
În figura 3, una dintre aceste raze este construită. Primul con generatoarea BA1 definit și axa perpendiculară pe planul π1, iar al doilea con - generatoarea BA2 și axa perpendiculară pe planul π2. Pentru construirea liniei dorite există până acum doar punctul B, vârful comun al conurilor. Al doilea punct, punctul K, este comun suprafețelor acestor conuri, găsim cu ajutorul unei sfere cu centru la punctul B.
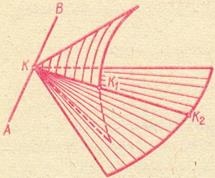
Un alt exemplu, atunci când un proces de construire a proprietății intersecție se utilizează cele două suprafețe conice cu un vârf comun al liniei lor drepte comune - generatoarea de construcție care formează suprafața este exclusă, numit un cilindru cu trei ghid. Să arătăm (fig.4) că în numărul de ghidaje o linie dreaptă AB și două linii curbe. Dacă luăm punctul (A), pe ghidajul linie dreaptă și luați-o ca un nod comun suprafețe conice auxiliare pentru care curbele de date servesc drept ghizi, linia de intersecție a acestor suprafețe conice, care trece prin vârf, cruci și ghidurile lor, care este, va fi direct la cilindrul cu trei ghiduri. Evident, trebuie să luăm o serie de puncte ale unei linii date și să executăm pentru fiecare dintre ele construcția de mai sus, care va da o serie de generatoare de cilindri cu trei ghidaje.
Dacă pentru această suprafață toate cele trei curbe de ghidare, atunci această metodă de construcție rămâne aceeași: punctele care servesc drept vârfuri pentru suprafețele conice auxiliare sunt luate pe una din aceste curbe.
2. În intersecția suprafețelor de rotație de ordinul doi, în unele cazuri se obține descompunerea liniei de intersecție în două curbe plane de ordinul doi. Acest lucru se întâmplă în cazul în care ambele suprafețe de intersecție (un cilindru și un con, două conuri, un elipsoid și un con etc.) sunt descrise în jurul unei sfere comune pentru ei. În exemplele prezentate în fig. 5, în primele trei cazuri de intersecție are loc de-a lungul elipsei, în al patrulea - prin elipse și parabola, iar în al cincilea - prin elipse și hiperbola.
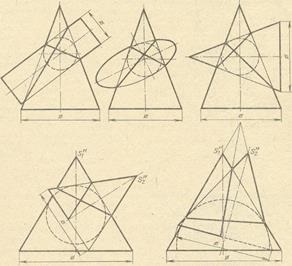
În Fig. 6 prezintă doi cilindri de diametru egal cu axe intersectate. Din punctul de intersecție a axelor, poate fi trasă o sferă înscrisă în ambele cilindri. Ambele suprafețe se intersectează de-a lungul unei linii formate din două elipse. În Fig. 6 din dreapta arată și doi cilindri cu diametrul egal, dar axele lor se intersectează de data aceasta nu în unghi drept. Linia de intersecție este formată din jumătate din două elipse.
Reprezentată în Fig. 5 și 6 curbe ale suprafețelor de intersecție sunt proiectate pe planul frontal al proiecției în formă de segmente de linie dreaptă, ca un plan comun de simetrie al fiecărei perechi de suprafețe este aranjată paralel cu planul π2 considerat.
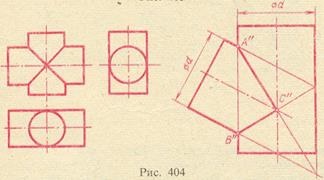
In exemplele de mai sus, există un contact dublu a două suprafețe intersectate de ordinul al doilea, adică prezența acestor suprafețe ale celor două puncte de atingere, și deci cele două planuri, fiecare dintre care atinge ambele suprafețe punctul lor totală. Noi nu dau nici o dovadă a următoarelor două poziții, care se bazează pe construcția menționată mai sus: 1) o a doua suprafață de comandă a avea contact dublu, se intersectează două curbe de ordinul doi, cu planul curbelor trec prin linia determinat punctele de contact; 2) două suprafețe Quadric descrisă de ordinul al doilea despre a treia cu fața (sau înscrisă în ea (de exemplu, două elipsoid comprimat de revoluție înscrisă în suprafața sferică)) intersectează două curbe de ordinul doi. A doua propoziție, cunoscută sub numele de teoria lui Monge, vine de la prima.
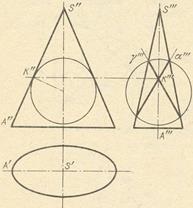
Pe baza celor de mai sus, se pot găsi secțiunile circulare ale unui con elliptic și unui cilindru eliptic. Un exemplu este dat în Fig. 7. Unele sfere sunt luate astfel încât să aibă un contact dublu cu suprafața conului eliptic. În intersecția unei sfere cu un con, se obțin două curbe plane - cercuri în planuri de tăiere a profilului # 947; și # 945; dau două sisteme de secțiuni circulară ale unui con elliptic.
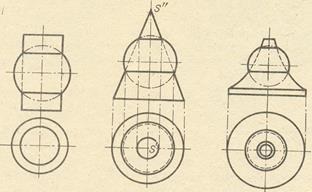
3. Sursele coaxiale de revoluție (adică suprafețe cu o axă comună) se intersectează de-a lungul cercurilor. În Fig. 8 sunt trei exemple: a) un cilindru și un con, b) elipsoid comprimat, un trunchi de con, c) două sfere. În toate aceste exemple sunt date doar proiecții frontale, iar axa comună a suprafețelor este paralelă cu planul π2. Prin urmare, cercurile obținute prin trecerea unei suprafețe cu cealaltă sunt proiectate pe π2 sub formă de segmente rectilinii.
Pentru axa sferei, puteți lua orice diametru. Prin urmare, sferele intersectante sunt considerate suprafețe coaxiale de revoluție. De asemenea, așa cum se arată în Fig. 9 cilindru și sferă, con și sferă, o anumită suprafață de rotație și sferă. Axele cilindrului, conului și suprafeței de rotație trec prin centrele sferelor. Intersecția are loc de-a lungul cercurilor.
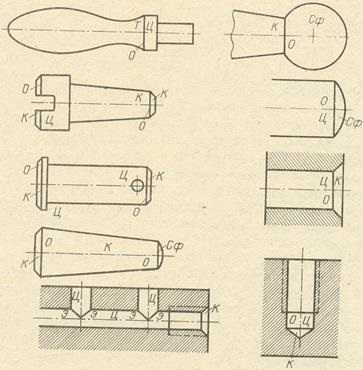
În Fig. 10 oferă exemple ale imaginii suprafețelor coaxiale de rotație și contra-foraj a aceluiași diametru din practicarea desenului tehnic. Suprafețele sunt notate cu literele: T este un inel circular, K este un con, U este un cilindru, C este o sferă; Liniile obținute la intersecția liniei sunt indicate prin literele: O - cerc, E - elipsă. Aceste linii sunt proiectate sub formă de segmente rectilinie, grăsimea Kuk a axei suprafețelor este paralelă cu planul proeminențelor (în acest caz, planul π2).
Ca urmare a cercetării noastre, noi:
· Dezvoltarea conceptului de aranjare reciprocă a suprafețelor în spațiu
· Studierea formelor posibile de intersecție a suprafețelor în spațiu
· Am învățat cum să construim linii de intersecție a suprafețelor curbe
Cred că această lucrare este utilă pentru studenții interesați de matematică și poate fi folosită în clasele opționale de geometrie.
LISTA LITERATURII UTILIZATE
1. Anisimov IK Rezumate ale prelegerilor privind geometria descriptivă. - R. 1970.
2. Hilbert. D. Geometria vizuală. - M. Nauka, 1981.
3. Gordon V.O. Curs geometrie descriptivă. - M. Nauka, 1988.
4. Frolov, S. A. Geometria descriptivă: un manual pentru licee. - M. Machine Building, 1983.
Vă mulțumim pentru ajutor! Luați o pauză, student, aici ați avut o bună dispoziție: Profesor la examen: Mai devreme, în tinerețe, eram furios - am umplut studenții numai în felul acesta, dar acum am devenit vechi, potrivite. ia o carte de carte a unui student, vino să te reia. Apropo, un anecdot este luat de chatanekdotov.ru