

Soluția pas-cu-pas a problemei 10 - intersecția unui torus circular și a unui cilindru
Problema nr. 10 este de asemenea dedicată temei construirii unei linii de intersecție a suprafețelor - un torus și un cilindru. Acestea sunt sarcinile cele mai complexe și consumatoare de timp care necesită cunoașterea metodelor de construire a liniilor de intersecție a diferitelor suprafețe.
Pentru a rezolva problemele trebuie să știm:
- metode de specificare a suprafeței într-un desen complex;
- metode pentru construirea liniei de intersecție a suprafețelor în probleme de geometrie descriptivă:
a) metoda planului de tăiere;
b) metoda generatoarelor;
c) metoda mediatorului cu bile (bile concentrice și excentrice).
Procedura de rezolvare a problemelor
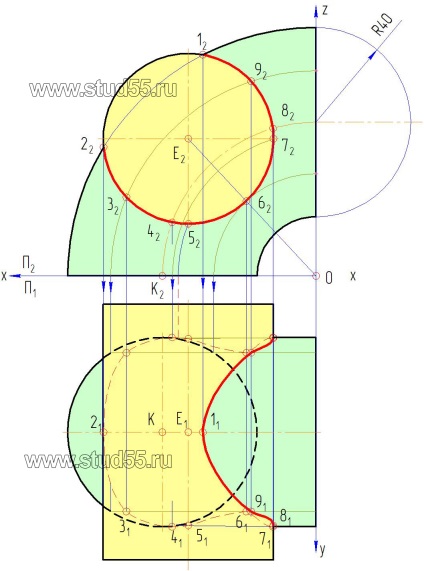
1. Conform variantei sarcinii pe coordonatele punctelor, construim în două proeminențe suprafețele unui cilindru circular drept și un torus deschis (a patra parte a acestuia) în linii subțiri sau ca în Fig. 10.1.
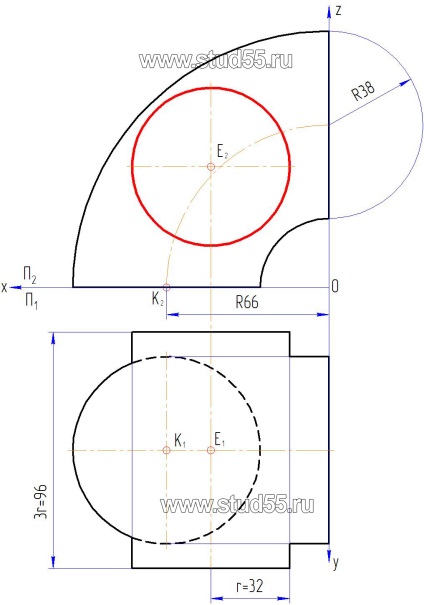
2. Pentru a construi linia de intersecție se aplică metoda generatoarelor (metoda planului de tăiere a fost considerată mai devreme), fiind cea mai potrivită pentru această problemă. Esența ei constă în faptul că pe suprafața, care este prezentat într-o formă generală, un număr de generatoare, a marcat punctul de intersecție al generatoarelor de-a doua suprafață, care este dat o linie de intersecție a acestor suprafețe (este un front-proeminentă). Următoarele sunt proiecțiile acestor generatoare și proiecțiile punctelor proeminențelor situate pe ele pe planul conjugat. Conectându-le cu o linie netedă, obținem linia dorită de intersecție a suprafețelor date.
Astfel, în problemă este necesar să se construiască o linie de intersecție a unui cilindru circular drept și a unei suprafețe torus (un sfert dintr-un torus deschis). Problema este rezolvată în următoarea ordine:
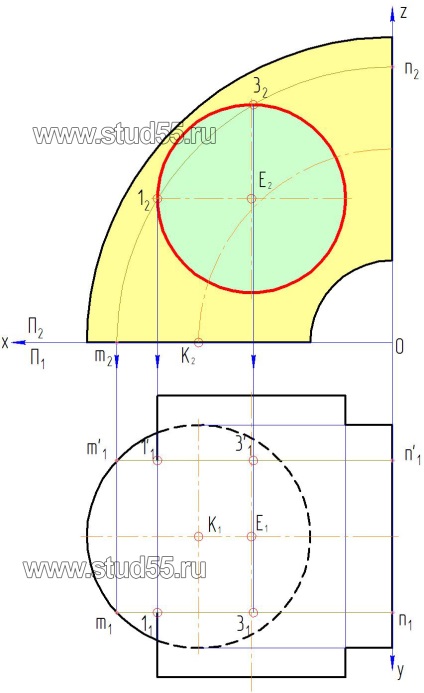
a) desenăm primul generator m2n2 în planul frontal al proeminențelor P2 de-a lungul suprafeței torusului. Se marchează proiecțiile punctelor de intersecție a acesteia cu suprafața cilindrică 12 = 1'2 și 32 = 3'2. Pentru punctul 12, luăm punctul de tangență al suprafeței cilindrice de la generatorul extrem de stâng al torului (vezi Figura 10.2);
c) transferăm (proiectăm) punctele de intersecție ale generatorului de pe suprafața cilindrică a planului frontal la planul orizontal, obținem 12 -1'2 și 32 -3'2. Aceasta este proiecția punctelor aparținând liniei de intersecție a suprafețelor, deoarece ele aparțin simultan pe suprafețele torus și cilindrice.
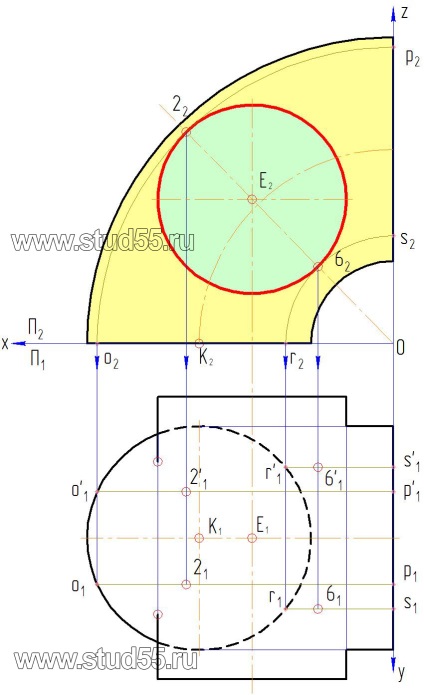
Pentru următoarele două puncte sunt două perechi de fire care formează o2p2ir2s2 în partea de sus și de jos, cu o suprafață cilindrică tangentă într-un punct 22 și 62. Pentru a obține proiecțiile de puncte pe P2. Acesta trebuie să fie prin centrul de proiecție 0 și E2 trage o linie dreaptă, și în locuri unde se intersectează conturul suprafeței cilindrului, obținem punctele de proiecție dorite 2 și 6. Repetați toți pașii stabilite la punctele „a“, „b“, „c“.
d) formarea unui conductor suplimentar prin prin intervalul selectat sau) punct specific (referința suprafețelor, în acest exemplu prin intermediul punctelor de sprijin (Fig. 10.3).
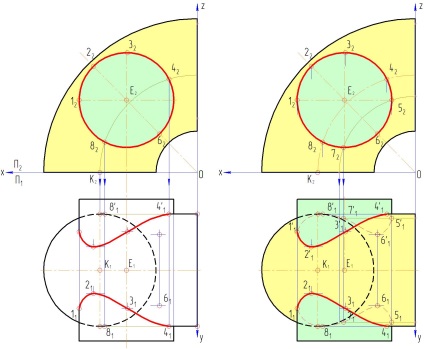
3. Proiecțiile rezultate ale punctelor din planul orizontal sunt conectate secvențial de-a lungul ramurilor paralele și drepte ale curbei netede, luând în considerare vizibilitatea ambelor suprafețe simultan - aceasta este linia de intersecție a suprafețelor date. Vizibilitatea sa se determină pe baza faptului că punctele vizibile sunt toate punctele, proiecția orizontală a suprafeței cilindrice, care în proiecția frontală sunt mai mari decât diametrul cilindrului. Pentru suprafața torusului, punctele din proiecția orizontală vor fi vizibile, care în partea frontală sunt situate mai sus și spre stânga axei torusului (axa torusului, precum și diametrul cilindrului, sunt limitele vizibilității). Punctele rămase pentru cilindru și pentru torus vor fi invizibile (Figura 10.4).
4. Trebuie remarcat, după cum sa menționat anterior, că intersecția suprafețelor poate fi completă și incompletă. Dacă intersecția este incompletă, linia de intersecție are o buclă închisă (exemplul problemei luate în considerare), cu o intersecție completă, linia de intersecție se împarte în mai multe bucle închise (în esență două). Construcția lor se realizează prin aceeași metodă ca cea prezentată în prezenta problemă.
După construirea intersecției suprafețelor, părțile vizibile ale liniei de intersecție și contururile vizibile corespunzătoare ale suprafețelor sunt în cele din urmă îndepărtate de liniile de contur; linii invizibile (punctate) sunt atribuite tuturor celorlalte linii.
Secțiune: Geometrie descriptivă /