Un produs scalar al vectorilor u este un număr egal cu produsul lungimilor acestor laturi de cosinusul unghiului dintre ele.
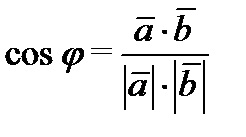
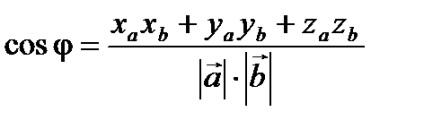
Dacă vectorii sunt în formă de coordonate. .
atunci produsul lor scalar se calculează cu formula:
Proprietățile unui produs scalar:
Produs vector de vectori. Proprietăți. Aplicație.
Un vector vector al vectorilor u este un vector. îndeplinind următoarele condiții:
1). unde j este unghiul dintre vectori și.
2) vectorul este ortogonal față de vectorii u
3). și formează triple-dreapta vectorilor.
Proprietățile produsului vectorial al vectorilor
5) Vedeți vectori într-un sistem de coordonate dreptunghiulare carteziană cu vectori de unitate.
-coordonatele axelor de coordonate Ox, Oy, Oz, respectiv:
6) Semnificația geometrică a produsului vectorial al vectorilor este aria paralelogramului construit pe vectori și. .
Notă: dacă doriți să scăpați zona unui paralelogram, trebuie să numărați mai întâi,
Produs mixt de vectori. Proprietăți. Aplicație.
Un produs mixt de trei vectori
Un produs mixt are următoarele proprietăți:
1). dacă toți cei trei vectori sunt paralele cu același plan (coplanar);
2) permutarea ciclică
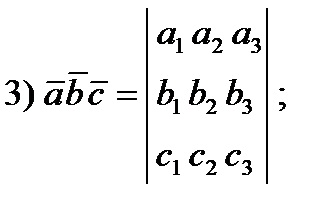
4) volumul unui paralelipiped construit pe vectori și. este
dacă a * b * c> 0, atunci triple a, b, c are dreptate dacă a * b * c<0, то тройка a,b,c - левая
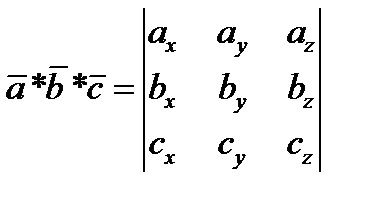
Starea coplanarității cu 3 vectori.
Bazele vectorilor. Coordonatele vectorului. Extinderea vectorului în raport cu baza.
Baza este grupul in-in b / w exprimă tot spațiul lin. În spațiul tridimensional, baza constă din 3 elemente ne-coplanare. În spațiul de 2 v-ra.
Baza ortogonală constă în baze reciproc perpendiculare. ()
Baza normalizată constă în vectorii unitari ().
În mod implicit, se ia o bază ortogonală.
Extindere pe bază:
-proiecție sau coordonare.
13. Condiții de colinearitate, ortogonalitate, coplanaritate a vectorilor.
Condiția de ortogonalitate pentru vectori
Doi vectori sunt ortogonali cu condiția ca produsul lor scalar să fie egal cu zero:
Starea colinearității vectorilor
Dacă vectorii sunt coliniari (se află pe o linie sau pe linii paralele). unghiul dintre ele este 0 sau 180 0. atunci produsul lor vectorial este egal cu zero:
Starea coplanarității vectoriale
Vectorii sunt coplanari (situați în același plan) dacă produsul lor mixt este egal cu zero:
Operatori liniari. Valorile proprii și vectorii proprii ai unui operator liniar. Modele de schimb liniar.
peste câmpul P, este un operator liniar dacă
1) pentru orice vector
2) pentru orice vector și orice altceva.
Vectorii proprii și valorile proprii ale unui operator liniar.
1) Matricea unui operator liniar:
lăsa # 966; -L.O. a unui spațiu vectorial V deasupra unui câmp P și a uneia dintre bazele V:
lăsa
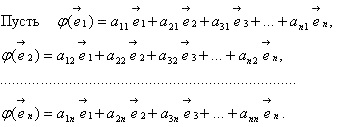
Apoi matricea LO # 966;:
2) Legătura dintre matricile unui operator liniar în diferite baze:
M (# 966;) este matricea LO. # 966; în vechea bază.
M1 (# 966;) este matricea LO. # 966; într-o nouă bază.
T este matricea de tranziție de la cea mai înaltă bază la noua bază.
2) Acțiuni asupra operatorilor liniari:
lăsa # 966; și f sunt LO diferite. spațiu vector V.
atunci # F + f este suma operatorilor liniari # 966; și f.
k · # 966; - multiplicare LO la scalar k.
# F este produsul operatorilor liniari # 966; și f.
Sunt, de asemenea, LA. spațiu vector V.
4) Kernel-ul operatorului liniar:
d (# 966;) este dimensiunea nucleului LO. # 966; (Defect).
5) Imaginea unui operator liniar:
a alergat # 966; - rangul L.O. # 966; (dimensiunea lui Jm # 966;).
6) Vectorii proprii și valorile proprii ale unui vector liniar:
# 61623; lăsa # 966; - L.O. vector spațiu V peste câmpul P și u
Dacă asta # 955; - valoarea proprie
- eigenvector al LO # 966; răspunzând # 955;
# 61623; Ecuația caracteristică a L.O. # 966;:
# 61623; Setul de vectori proprii care corespund valorii proprii # 955;:
# 61623; LO vector spațiu sunt numite LO. cu un spectru simplu dacă # 966; dacă # 966; are exact n valori proprii.
# 61623; În cazul în care # 966; - L.O. cu un spectru simplu, atunci are o bază de vectori proprii în raport cu care este matricea AO. # 966; este diagonală.